Partie B – Étude énergétique d’une chandelle
Par une modélisation numérique, on cherche à calculer la vitesse du
ballon lorsqu’il est
récupéré par le joueur. Pour cela, on effectue une étude énergétique du
système défini dans
la partie A à l’aide d’un programme en langage Python dont un extrait
est présenté cidessous. Ce programme utilise les coordonnées x(t) et
z(t) du vecteur position et v
x
(t) et
v
z
(t) du vecteur vitesse obtenues par modélisation de la trajectoire du ballon.
Les variables x, z, v
x et v
z sont déclarées dans le code mais non affichées dans l’extrait suivant :

L’exécution de ce programme permet d’obtenir le graphique suivant
qui modélise l’évolution des énergies du point G au cours du temps.
6. Relever dans le code la valeur de la masse du ballon.
m=0,440 kg.
7. Identifier les grandeurs calculées aux lignes 26 et 27.
ligne 26 : vitesse v.
ligne 27 : énergie cinétique.
8. Recopier et compléter le code des lignes 27, 28 et 29 du programme.
ligne 27 :Ec = 0.5*m*v**2
ligne 28 : Ep=m*g*z.
ligne 29 Em=Ec+Ep
9. En justifiant, attribuer la nature de l’énergie correspondant à chaque courbe du
graphique suivant.
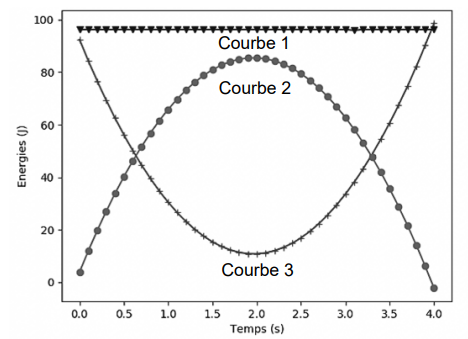
Courbe1 : énergie mécanique constante.
Courbe 2 : l'énergie potentielle augmente puis décroït.
courbe3 : l'énergie cinétique diminue lors de la montée puis augmente lors de la descente.
10. Indiquer, en expliquant, si l’hypothèse sur les frottements de l’air, proposée au début de
l’exercice, a été prise en compte dans la modélisation numérique.
L'énergie mécanique étant constante, les forces de frottement n'ont pas été prise en compte.
Le joueur tape le ballon et lui communique une vitesse initiale v
0 dont la valeur est celle de
la partie A. Il récupère le ballon à une altitude de 2,90 m.
11. À l’aide d’une étude énergétique, calculer la vitesse du ballon, en km·h
–1
, lorsqu’il est
récupéré par le joueur.
Energie cinétique initiale : 0,5 x0,44 x 20,5
2 =92,455 J.
Energie potentielle initiale : 0,44 x9,81 x0,90=3,885 J.
Energie mécanique : 92,455 +3,885 =96,34 J.
Energie potentielle final : 0,44 x9,81 x 2,90 =12,52 J.
Energie cinétique finale : 96,34 -12,52 =83,82 J.
Vitesse finale : ½mv
2 =83,82.
v
2 = 2 x83,82 / 0,44 =381 ; v = 19,52 m /s ou 19,52 x3,6 =70,3 km / h.