Mathématiques. Bac Polynésie 02 / 09 /2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
Exercice 1. 5 points.
En France il y a deux formules pour obtenir le permis de conduire :
- Suivre à partir de 15 ans une formation de conduite accompagnée pendant 2 ans;
- Suivre la formation classique (sans conduite accompagnée) à partir de 17 ans.
En France actuellement, parmi les jeunes qui suivent une formation au permis de conduire,
16 % choisissent la formation de conduite accompagnée, et parmi eux, 74,7 % réussissent l’examen de conduite dès leur première tentative.
En suivant la formation classique, le taux de réussite dès la première tentative est seulement de 56,8 %.
On choisit au hasard un jeune français qui a déjà passé l’examen de conduite et on considère les évènements A et R suivants :
- A : « le jeune a suivi la formation de conduite accompagnée »;
-  R : « le jeune a eu le permis dès sa première tentative ».
On arrondira les résultats à 10−3 près, si nécessaire.
Partie A
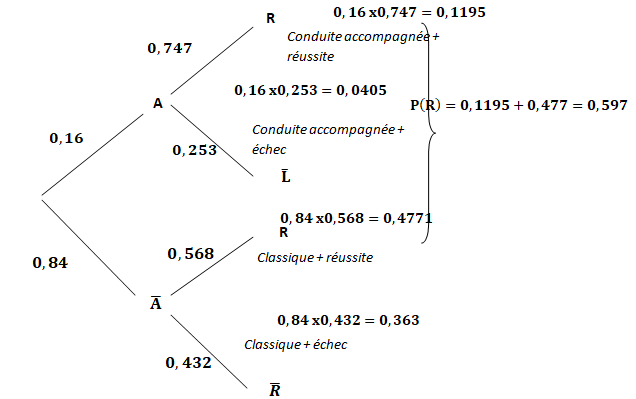
1. Dresser un arbre de probabilités modélisant cette situation.
2. a. Démontrer que P(R) = 0,59664.

Dans la suite, on gardera la valeur 0,597 arrondie à 10−3 près.
b. Donner ce résultat en pourcentage et l’interpréter dans le contexte de l’exercice.
59,7 % réussissent l'examen la première fois.
3. On choisit un jeune ayant eu son permis dès sa première tentative. Quelle est la probabilité qu’il ait suivi la formation de conduite accompagnée ?
PR(A) = P(R n A) / P(R)=0,1195 / 0,597=0,200.
4. Quelle devrait être la proportion de jeunes suivant la formation de conduite accompagnée si on voulait que le taux de réussite global (quelle que soit la formation choisie) dès la première tentative à l’examen de conduite dépasse 70 %?
0,747 x+ 0,568 (1-x) > 0,70.
0,179 x >0,132 ; x >0,737.

Partie B
Une auto-école présente pour la première fois à l’examen de conduite 10 candidats qui ont suivi la formation de conduite accompagnée. On modélise le fait de passer les examens de conduite par des épreuves aléatoires indépendantes.
On note X la variable aléatoire donnant le nombre de ces 10 candidats qui auront leur permis dès la première tentative.
1. Justifier que X suit une loi binomiale de paramètres n = 10 et p = 0,747.
Il s'agit d'une répétition de facon indépendante d'une même épreuve de Bernoulli de paramètre n = 10 et p =0,747
2. Calculer P(X >6). Interpréter ce résultat.
P(X >6) = 1-P(X < 5)=0,918.
La probabilité que plus de 6 candidats réussissent l'examen pour la première fois est égale à 0,918.
3. Déterminer E(X) et V (X).
E(X) = n p = 10 x0,747 = 7,47.
V(X) = n p(1-p)=10 x0,747 x(1-0,747)=1,89.
4. Il y a aussi 40 candidats qui n’ont pas suivi la formation de conduite accompagnée et qui se présentent pour la première fois à l’examen de conduite. De la même manière, on note Y la variable aléatoire qui donne le nombre de ces candidats qui
auront le permis à la première tentative. On admet que Y est indépendante de la variable X et qu’en fait E(Y ) = 22,53 et V (Y ) =9,81.
On note alors Z la variable aléatoire comptant le nombre total de candidats (parmi les 50) qui auront le permis de conduire dès la première tentative dans cette autoécole.
a. Exprimer Z en fonction de X et Y . En déduire E(Z) et V (Z).
Z = X + Y.
E(Z) = E(X) + E(Y) = 7,47 +22,53=30.
V(Z) =V(X)+V(Y) =1,89 + 9,81=11,7.
b. En utilisant l’inégalité de Bienaymé-Tchebychev, montrer que la probabilité qu’il y ait moins de 20 ou plus de 40 candidats qui aient leur permis dès la première tentative est inférieure à 0,12.
P(|Z-E(Z) | > a) < V(Z) / a2 .
P(|Z-30 | > a) < 11,7 / a2 .
P((Z < 20) union Z > 40))=P((Z-30 < -10 union (Z-30 > 10))= P(|Z-30| > 10)= < 11,7 /102 soit inférieure à 0,12.

Exercice 2. 5 points.
On étudie l’évolution de la population d’une espèce animale au sein d’une réserve naturelle.
Les effectifs de cette population ont été recensés à différentes années. Les données collectées sont présentées dans le tableau suivant :
Année
 2000
 2005
 2010
 2015
Nombre d'individus
 50
 64
 80
 100
Pour anticiper l’évolution de cette population, la direction de la réserve a choisi de modéliser le nombre d’individus en fonction du temps. Pour cela, elle utilise une fonction, définie sur l’intervalle [0 ; +∞[, dont la variable x représente le temps écoulé, en année, à partir de l’année 2000. Dans son modèle, l’image de 0 par cette fonction vaut 50, ce qui correspond au nombre
d’individus en l’an 2000.
Partie A..Modèle 1
Dans cette partie, la direction de la réserve fait l’hypothèse que la fonction cherchée satisfait l’équation différentielle suivante :
y′=0,05y −0,5 (E1)
1. Résoudre l’équation différentielle (E1) avec la condition initiale y(0) =50.
Solution générale de y'-0,05y=0 : f(t) =A exp(0,05 t) avec A une constante réelle.
Solution particulière de (E1) : g(t) = 10.
Solution générale de (E1) : f(t) +g(t) =A exp(0,05 t) +10.
A t=0 : 50 = A+10 ; A = 40.
f(t) +g(t) =40 exp(0,05 t) +10.
2. Comparer les résultats du tableau avec ceux que l’on obtiendrait avec ce modèle.
Année
 2000
 2005
 2010
 2015
Nombre d'individus (modèle 1)
 50
 61
 76
 95
Ces valeurs sont inférieures aux valeure réeelles.

Partie B.Modèle 2
Dans cette partie, la direction de la réserve fait l’hypothèse que la fonction cherchée satisfait l’équation différentielle suivante :
y′=0,05y(1−0,00125y)
On note f la fonction définie sur [0 ; +∞[ par : f (x) =800 / (1+15 exp(-0,05x)) et C sa courbe représentative dans un repère orthonormé.
1. Démontrer que la fonction f vérifie f (0) = 50 et que pour tout x réel : f ′(x) = 0,05 f (x)(1−0,00125f (x)).
On donne : f '(x) = 600 exp(-0,05x) / (1+15 exp(-0,05x))2.
f(0) = 800 / (1+15) =50.
0,00125 f(x) = 1 / (1+15 exp(-0,05x)).
1-0,00125f(x) = 1-1 / (1+15 exp(-0,05x))=15 exp(-0,05x)) / (1+15 exp(-0,05x)).
0,05f (x)(1−0,00125f (x)).=0,05 *800 *15 exp(-0,05x)) / (1+15 exp(-0,05x))2= 600 exp(-0,05x) / (1+15 exp(-0,05x))2.

On admet que cette fonction f est l’unique solution de (E2) prenant la valeur initiale de 50 en 0.
2. Avec ce nouveau modèle f , estimer l’effectif de cette population en 2050. Arrondir le résultat à l’unité.
x = 50 ; f (50) =800 / (1+15 exp(-0,05*50))=359.
3. Calculer la limite de f en +∞. Que peut-on en déduire quant à la courbe C ? Interpréter cette limite dans le cadre de ce problème concret.
Le terme en exponentielle tend vers zéro et f(x) tend vers 800.
La droite d'équation y = 800 est asymptote à la courbe C.
Le nombre d'individus tend vers 800 au bout d'un temps suffisamment long.
4. Justifier que la fonction f est croissante sur [0 ; +∞[.
La dérivée f '(x) est positive ; la fonction f(x) est croissante sur [0 ; +∞[.
5. Démontrer le résultat obtenu en ligne 4 du logiciel.
15 exp(-0,05x)-1 > 0 ; exp(-0,05x) > 1/15 .
-0,05x > ln(1/15) ; -0,05 x > -ln(15) ; x < ln(15) / 0,05 ; x < 20 ln(15).
6. On admet que la vitesse de croissance de la population de cette espèce, exprimée en nombre d’individus par an, est modélisée par la fonction f ′.
a. Étudier la convexité de la fonction f sur l’intervalle [0 ; +∞[ et déterminer les coordonnées des éventuels points d’inflexion de la courbe C.
On donne f "(x) = 30 exp(-0,05x) (15 exp(-0,05x)-1) / (1+15exp(-0,05x))3.
La dérivée seconde a le signe de 15 exp(-0,05x) -1.
Si x < 20 ln(15) : f "(x) >0  et f(x) est convexe.
Si x > 20 ln(15) : f "(x) < 0  et f(x) est concave.
Si x = 20 ln(15), il y a un point d'inflexion.
f (20 ln(15)) =800 / (1+15 exp(-ln(15)))=800 / (1+1)=400.

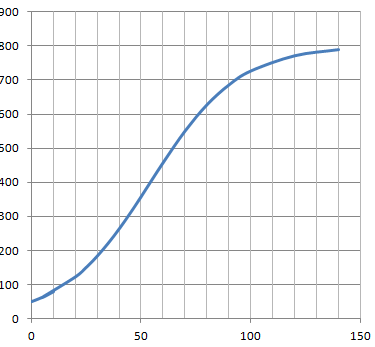
b. La direction de la réserve affirme :
«Au vu de ce modèle, la vitesse de croissance de la population de cette espèce va augmenter pendant un peu plus cinquante ans, puis va diminuer ». La direction a-t-elle raison? Justifier.
La vitesse de croissance correspond à la valeur de la dérivée première à la date considérée.
Si x < 20 ln(15) : f "(x) >0  et f '(x) est croissante.
Si x > 20 ln(15) : f "(x) < 0  et f '(x) est négative.
La direction a raison.

... =  =
....

 Exercice 3. 5 points.
On considère la suite (un) définie par u0 = 5 et, pour tout entier naturel n :
un+1 = 2+ln(un2-3)
On admet que cette suite est bien définie.
Partie A : Exploitation de programmes Python
1. Recopier et compléter le script Python ci-dessous pour que suite(k) qui prend en paramètre un entier naturel k, renvoie la liste des k premières valeurs de la suite (un).
Remarque : On précise que, pour tout réel strictement positif a, log(a) renvoie la valeur du logarithme népérien de a.
def suite(k):
L = [0]
u = 5
for i in range(k):
L.append(u)
u=2+log(u**2-3)
return(u)
2. On a exécuté suite(9) ci-dessous. Émettre deux conjectures : l’une sur le sens de variation de la suite (un) et l’autre sur son éventuelle convergence.
5, 5.0910, 5.13195, 5.15003, 5.15797, 5.161, 5.1629, 5.1636, 5.1639.
La suite est croissante et converge vers un réel compris entre 5,16 et 5,17..
3. On a ensuite créé la fonction mystere(n) donnée ci-dessous et exécuté mystere(10000), ce qui a renvoyé 1.
Cet affichage contredit-il la conjecture émise sur le sens de variation de la suite (un) ? Justifier.
def mystere(n):
L = suite(n)
c = 1
for i in range(n - 1):
if L[i] > L[i + 1]:
c = 0
return c
>>> mystere(10000)
1
La fonction mystère indique 1 si la suite est croissante et 0 s'il existe un rang k à partir duquel uk > uk+1 parmi les n premiers termes de la suite. L'affichage de 1 contredit la conjecture émise sur le sens de variation de la suite.
Partie B : Étude de la convergence de la suite ( un )
On considère la fonction g définie sur [2 ; +∞[ par :
g(x) =2+ln(x2-3)
On admet que g est dérivable sur [2 ; +∞[ et on note g′ sa fonction dérivée.
 1. Démontrer que la fonction g est croissante sur [2 ; +∞[.
Calcul de la dérivée g'(x) en posant u = x2-3 ; u'=2x.
g'(x) = u'/u=2x /(x2-3).
Sur [2 ; +∞[, g'(x) est positive et g(x) est strictement croissante.
2. a. Démontrer par récurrence que, pour tout entier naturel n :
4<un <un+1 < 6.
Initialisation : u0=5 ; u1 =2+ln(52-3)~5,09. La propriété est vraie au rang 1.
Hérédité : 4<un <un+1 <6 est supposée vraie.
g(x) étant strictement croissante sur [2 ; +oo[ : g(4) < g(un) < g(un+1) < g(6).
g(4) < un+1 < un+2 < g(6) ;
g(4) =2+ln(7)~4,56 ; g(6)~5,5
4,56 < un+1 < un+2 < 5,5 ;
 4 < un+1 < un+2 < 6 ;.
Conclusion : la propriété est vraie au rang 0 et héréditaire, elle est donc vraie pour tout entier naturel n.
b. En déduire que la suite (un) converge.
La suite est croissante et bornée, donc elle converge.

Partie C : Étude de la valeur de la limite
On considère la fonction f définie sur [ 2; +∞[ par :
f (x) =2+ln(x2-3)-x.
On admet que f est dérivable sur [2 ; +∞[ et on note f ′ sa fonction dérivée.
On donne le tableau de variations de f suivant. On ne demande aucune justification.

1. a. Montrer que l’équation f (x) = 0 admet exactement deux solutions sur [2 ; +∞[ que l’on notera a et ß avec a <β.
La fonction f est continue sur [ 2 ; 3] et le nombre 0 appartient à l'intervalle image [0 ; ln(6)-1].
D'après le théorème des valeurs intermédiaires, l'équation f(x) =0 possède une solution a = 0.
La fonction f est continue sur [ 3 ; +oo[ et le nombre ln(6)-1 ~0,79  appartient à l'intervalle image [0,79 ; -oo[.
D'après le théorème des valeurs intermédiaires, l'équation f(x) =0 possède une solution ß .
b. Donner la valeur exacte de a et une valeur approchée à 10−3 près de β.
ß =5,164.
2. On note l la limite de la suite (un).
Justifier que f (l) = 0 et déterminer l.
l est solution de l'équation g(x) =x  ; g(x)-x) =0 ; f(x) = 0.
Donc l appartient à {0 ; ß}.
Or un > 5, donc l >5 ; l = ß.

Exercice4. 5 points.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse.
Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
1. On considère la fonction f définie sur ]0 ; +∞[ par : f (x) = x ln(x).
Affirmation 1 :  vrai.
on pose u = ln(x) et v'=x : u' = 1 /x et v =½x2.

Affirmation 2 : vrai. Soient n et k deux entiers naturels non nuls tels que k ≤ n.

 Pour les trois affirmations suivantes, on considère que l’espace est muni d’un repère orthonormé .
Soit d la droite de représentation paramétrique :
x = t+1 ; y = 2t+1; z = -t avec t réel.
Soit d' la droite de représentation paramétrique :
x = 2t'-1 ; y = -t'+2; z = t'+1 avec t' réel.
Soit P le plan d’équation cartésienne : 2x + y − 2z + 18 = 0.
Soit A le point de coordonnées (−1 ; −3 ; 2) et B le point de coordonnées (−5 ; −5 ; 6).
On appelle plan médiateur du segment [AB] le plan passant par le milieu du segment [AB] et orthogonal à la droite (AB).
Affirmation 3 : vrai. Le point A appartient à la droite d.
Si A appartient à la droite d :
-1=t+1 ; t=-2.
y=2*(-2)+1=-3= yA ; z = 2=zA.
Affirmation 4 : faux.  Les droites d et d’ sont sécantes.
Si les droites d et d' sont sécantes : t+1=2t'-1 ; t = 2t'-2.
2t+1 =-t'+2 ; 4t'-4=-t'+2 soit t' = 6 /5. Par suite t = 12/5-2=2/5.
z = -2,5 et z = 6 /5 +1 = 11 /5 diffère de -2,5.

Affirmation 5 : vrai. Le plan P est le plan médiateur du segment [AB].
Coordonnées du vecteur AB (-4 ; -2 ; 4).
Coordonnées du vecteur n normal au plan P : 2 ; 1 ; -2

Le plan P est orthogonal à la droite (AB).
Coordonnées du point C, milieu du segment (AB] :
(-5-1) /2 ; (-5-3) / 2 ; (6+2) / 2 soit -3 ; -4 ; 4.
Si le point C appartient au plan P :
2xC + yC − 2zC + 18 = 0.
-6-4-8+18=0 est vérifié, donc C appartient au plan P.
Le plan P passe par le milieu du segment (AB] et est orthogonal à la droite (AB). P est donc le plan médiateur du segment [AB].



  
menu