Mathématiques. DNB Nouvelle Calédonie 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . ... . . . . .. .. ...... ... Exercice 1. 15 points. Cet exercice est un questionnaire à choix multiples (QCM). Pour chaque question, une seule des trois réponses proposées est exacte. Sur la copie, indiquer le numéro de la question et la réponse A, B ou C choisie. Aucune justification n’est demandée. Aucun point ne sera enlevé en cas de mauvaise réponse Question 1.   Parmi les nombres suivants, lequel est premier ? 719 ; 965 ; 687. Un nombre premier possède deux diviseur, 1 et lui même. 965 n'est pas premier, il est divible par 5. 687 n'est pas premier, il est divisible par 3. Question 2. Quelle est l’aire de la figure ci-dessous ? 24 cm2 ; 140 cm2 ; 25 cm2. 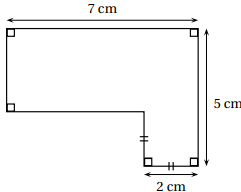Aire du rectangle de côtés 7 cm et 3 cm : 7 x3 = 21 cm2. Aire du carré de côté 2 cm : 2 x 2 = 4 cm2. Total : 25 cm2.   Question 3.   Une de ces fonctions est affine. Laquelle ? f(x) = 3(x+1) ; g(x) = 5 /x +1 ; h(x) = x2+1. Une fonction affine est du type f(x) = ax +b avec a et b réels. f(x) = 3x+3. Question 4. La distance de Tontouta à Narita est égale à environ 6 980 km. Le vol Tontouta-Narita dure environ 9 heures. Quelle est la vitesse moyenne, arrondie à la centaine de km/h, de l’avion sur ce trajet ? 600 ; 800 ; 1000. 6980 / 9 =775 ~800 km / h. Question 5. Dans un collège de 730 élèves, 60 % des élèves sont des filles. Quel est le nombre de filles dans ce collège ? 438 ; 60 ; 670. 730 x 0,60=438 filles. Exercice 2 : 20 points.   Thomas souhaite construire le cerf-volant représenté par la figure ci-dessous : 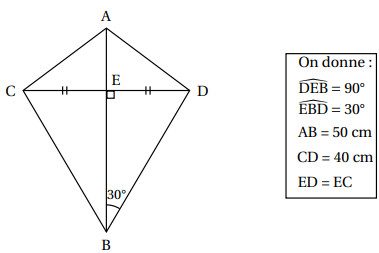1. Calculer BE. On donnera une valeur arrondie au millimètre. Rédiger la réponse en faisant apparaitre les différentes étapes. Dans le triangle rectangle BDE : tan 30 =ED / BE = 20 / BE. BE = 20 / tan 30 ~34,6 cm. Lorsque Thomas a essayé son cerf-volant, il s’est demandé à quelle altitude il volait. Il a attaché sa corde à un piquet planté dans le sol (point S) puis est allé se placer (point T) parfaitement à la verticale sous son cerf-volant (point H). Il a alors mesuré certaines longueurs et a réalisé le schéma suivant. 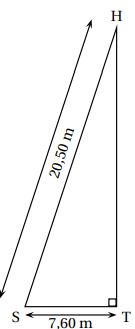2. Calculer HT, altitude à laquelle volait son cerf-volant. On donnera une valeur arrondie au mètre. Rédiger la réponse en faisant apparaitre les différentes étapes. Relation de Pythagore : HS2=ST2+HT2. HT2= HS2-ST2=20,52-7,62=362,49 ; HT = 19,03 ~ 19 m. Il est conseillé de ne pas utiliser ce cerf-volant lorsque le vent dépasse 20 km/h. La météo annonce un vent ne dépassant pas 15 nœuds. On donne 1 nœud = 0,514 m/s. 3. Thomas peut-il faire voler son cerf-volant sans risque dans ces conditions ? Justifier votre réponse. 15 x 0,514=7,71 m /s. 1 m/s = 3,6 km / h. 7,71 x3,6~27,8 km /h. Thomas ne doit pas faire voler son cerf-volant. ... =  = .... Exercice 3. 16 points.   On considère les programmes de calcul suivants : A. choisir un nombre ; ajouter 4 ; multiplier par 3. B :  choisir un nombre ; multiplier par 5 ; soustraire 3 ; soustraire le nombre de départ. 1. Dans cette question, on choisit le nombre 2 pour tester les deux programmes.  a. Vérifier par le calcul qu’on obtient 18 avec le programme A. 2+4=6 ; 6 x3 =18. b. Vérifier par le calcul qu’on obtient 5 avec le programme B. 2 x5 =10 ; 10-3=7 ; 7-2 =5.  2. Soit f la fonction associée au programme A, qui au nombre choisi x fait correspondre le résultat f (x). a. Justifier que f (x) = 3x +12.  f(x) = (x+4) *3 =3x+12. b. Calculer l’antécédent de 27 par la fonction f . 3x+12 = 27 ; 3x=27-12=15 ; x =15 /3 = 5. 3. Soit g la fonction associée au programme B, qui au nombre choisi x fait correspondre le résultat g(x). a. Donner l’expression de g(x). g(x) = 5 x-3-x= 4x-3.  b. Quel nombre faut-il choisir avec le programme B pour obtenir 2 comme résultat ? 2=4x-3 ; 4x = 5 ; x = 5 /4 =1,25. Hugo a choisi un nombre. Il l’a testé avec les deux programmes et a trouvé le même résultat à chaque fois. 4. Quel nombre a-t-il choisi ? f(x) = g(x= ; 3x+12=4x-3 ; 12+3=4x-3x ; 15 = x. EXERCICE 4 : Jeu de hasard 13 points Dans un jeu, les candidats doivent tirer une bille dans une boite et noter sa couleur, puis ils doivent ensuite lancer un dé de la couleur de la bille tirée et noter le résultat obtenu. Les issues de cette expérience sont donc des couples du type (couleur; nombre). Le matériel est le suivant : La boite contient des billes indiscernables au toucher : 15 rouges, 10 vertes et 5 bleues. Le dé rouge a 10 faces numérotées de 0 à 9. Le dé vert a 6 faces numérotées de 1 à 6. Le dé bleu a 4 faces numérotées de 1 à 4.  Pour gagner au jeu il faut obtenir 1 au lancé de dé.  1. Quelle est la probabilité de tirer une bille bleue dans la boîte ? 5 billes bleues sur 30 billes. Probabilité de tirer une bille bleue : 5 / 30 =1 / 6 ~ 0,17. 2. Amandine a tiré une bille verte et Alexis a tiré une bille rouge. Qui a le plus de chance de gagner à ce jeu ? Justifier. Amandine : probabilité de tirer une bille verte :10 /30 = 1 /3. Probabilité d'obtenir 1  : 1 /6. 1 /3 x 1 /6 = 1 / 18~0,0555. Alexis : probabilité de tirer une bille rouge :15 /30 = 1 /2 =0,5. Probabilité d'obtenir 1  : 1 /10 =0,1.. 0,1 x0,5 =0,05. Amandine a le plus de chance de gagner.  3. Donner l’ensemble des issues possibles de ce jeu. On notera « R » pour rouge, « V » pour vert et « B » pour bleu. Par exemple : l’issue (R; 3) correspond à : « la bille tirée est rouge et le résultat du lancer de dé est 3 ». (R ;0) ; (R ; 1) ; (R ; 2) ; (R ;3) ; (R ; 4) ; (R ; 5) ; (R ;6) ; (R ; 7) ; (R ; 8) ; (R; 9). (V ;1) ; (V ; 2) ; (V ; 3) ; (V ;4) ; (V ; 5) ; (V ; 6) (B ;1) ; (B ; 2) ; (B ; 3) ; (B ;4). EXERCICE 5 : Géométrie 20 points . La figure ci-dessous n’est pas à l’échelle 1. Prouver que les droites(BE) et (CD)sont parallèles. Les angles AEB et ADC sont des angles correspondants de même mesure : donc les droites (BE) et (CD) sont parallèles. 2. Calculer CD. Rédiger la réponse en faisant apparaitre les différentes étapes. Les triangles AEB et ADC sont semblables. Propriété de Thalès : AD / AE =CD / BE.  CD = AD x BE / AE = 15 x4 / 6=10 cm. 3. L’aire du triangle ABE, arrondie au dixième, est égale à 11,3 cm2 . En déduire l’aire du triangle ACD arrondie au dixième. Rapport de grandeur des triangles semblables AEB et ADC : 15 / 6 =2,5. Aire du triangle ACD = aire du triangle ABE x 2,52 = 11,3 x2,52 ~70,6 cm2. 4. Construire cette figure en vraie grandeur. Exercice 6 : 16 points. 1. Associer à chaque script ci-dessous la figure qui lui correspond. Sur la copie, indiquer le numéro du script et la figure correspondante. Script 1 : figure B. Script 2 : figure A. Script 3 : figure C. Le script ci-dessous commande la construction de la figure D. 2. Completer le script suivant qui commande la construction de la figure E.

menu