Mathématiques. DNB Amérique du Sud 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
... . .

.
.
.. ..
......


...
Exercice 1. 24 points.
 Les 5 situations suivantes sont indépendantes. On rappelle que, sauf indications contraires, les réponses doivent être justifiées.
 Situation 1.
 Décomposer 390 en produit de facteurs premiers.
390 = 2 x3 x5 x13
 Situation 2.
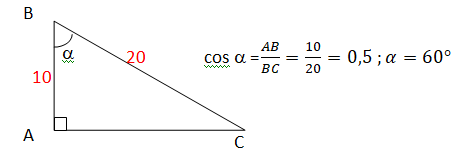
 ABC est un triangle rectangle en A avec AB = 10 cm et BC = 20 cm. Quelle est la mesure de l’angle ABC ?

  Situation 3.
 Une urne contient 12 jetons numérotés de 1 à 12 indiscernables au toucher. On pioche un jeton au hasard dans cette urne. Quelle est la probabilité d’obtenir un nombre inférieur ou égal à 5 ?
Cas favorables : 1 ; 2 ; 3 ; 4 ; 5.
Probabilité d’obtenir un nombre inférieur ou égal à 5 =5 / 12~0,42.
Situation 4.
On considère la fonction f dont on donne un tableau de valeurs et la représentation graphique ci-dessous :

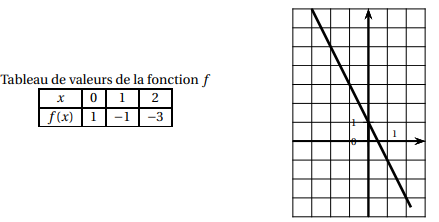1. Quelle est l’image de 2 par la fonction f ? (sans justifier)
f(2) = -3.
2. Quelle est l’image de −1 par la fonction f ? (sans justifier)
f(-1)=3.
3. La fonction f est-elle une fonction linéaire ?
Non, la droite ne passe pas par l'origine.

Situation 5. On considère l’égalité suivante : (2x −3)(4x +5) = 8x 2 −2x −15.
1. Montrer que cette égalité est vraie pour x = 2.
(2*2-3)(4*2+5)=1 *13 =13.
8 *22 -2*2-15= 32-4-15=13.
2. Cette égalité est-elle vraie quelle que soit la valeur de x ?
On développe : (2x −3)(4x +5) =8x2+10x-12x-15=8x 2 −2x −15.
L'égalité est vraie quel que soit x.

Exercice 2 : 20 points.
 Dans cet exercice, les deux parties sont indépendantes. Des élèves de 3e réalisent une enquête au sein de leur collège pour connaître le temps quotidien passé par leurs camarades sur les réseaux sociaux.
 Partie 1.
Voici la liste des durées (en minutes) recueillies auprès d’un groupe d’élèves : 135 ; 82 ; 104 ; 200 ; 102 ; 17 ; 143 ; 118 ; 62
1. Combien y a-t-il d’élèves dans ce groupe ? (sans justifier).
9 élèves.
 2. Calculer le temps moyen passé sur les réseaux sociaux par les élèves de ce groupe.
(135+82+104+200+102+17+143+118+62) / 9 =107 minutes.
3. Calculer l’étendue de cette série.
Duré la plus élevée - durée la plus courte =200-17=183 minutes.
4. L’affirmation suivante est-elle vraie ? « Plus de 50 % des élèves de ce groupe passent au moins 1 h 30 min par jour sur les réseaux sociaux. »
1 h 30 min = 90 minutes.
6 élèves sur 9  passent plus de 90 minutes sur les réseaux sociaux.
6 / 9 x100 ~67 %. Affirmation vraie.


 Partie 2.
 Le collège dans lequel l’enquête a été menée compte 640 élèves au total. 400 élèves ont répondu à l’enquête.
1. Vérifier que le nombre d’élèves ayant répondu représente plus de 60 % de l’effectif total du collège.
400 / 640 x100 =62,5 %.
Les résultats obtenus auprès des 400 élèves interrogés sont organisés par niveaux (6e , 5 e , 4e et 3e ) dans un fichier tableur dont voici une copie d’écran :

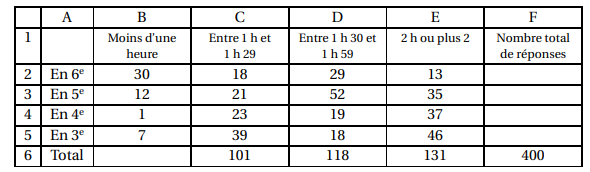2. Quelle formule peut-on entrer dans la cellule F2 afin de la recopier vers le bas jusqu’à la cellule F5 ? (sans justifier).
=(B2+C2+D2+E2) ou = Somme(B2 : E2)
 3. Combien d’élèves ayant répondu, passent moins de 1 h par jour sur les réseaux sociaux ?
30 +12 1 +7=50.
4. Calculer le pourcentage d’élèves, ayant répondu, qui passent moins de 1 h 30 min par jour sur les réseaux sociaux.
101+50 =151 élèves passent moins d'1h 30 min sur les réseaux.
151 / 400 x100 =37,75 %.

... =  =
....

 Exercice 3. 15 points.
 Dans cet exercice, aucune justification n’est attendue.
Une élève utilise un logiciel de programmation pour réaliser des dessins à partir d’un triangle équilatéral. Elle crée le bloc « triangle ».
1. Sur la copie, recopier et compléter les lignes 3 et 5 du bloc « triangle » afin qu’il dessine un triangle équilatéral.

Elle utilise maintenant le bloc « triangle » pour l’intégrer dans différents programmes.
 2. Associer chaque programme au dessin qu’il permet de réaliser. On indiquera sur la copie, le numéro du dessin et la lettre du programme associé.

Programme A et dessin 2 : le stylo est revenu en position initiale prêt à refaire le même triangle et on tourne de 90 degrés : le stylo dessine un triangle qui a tourné de 90 degrés.
Programme B avec dessin 3 : le stylo est revenu en position initiale prêt à refaire le même triangle, mais on avance de la longueur d’un coté.
3. On s’intéresse maintenant au programme ci-dessous. En prenant 1 cm pour 10 pas, construire sur la copie le dessin obtenu lorsque le programme s’exécute.


Exercice 4 : 20 points.
 On considère la figure ci-dessous qui n’est pas représentée en vraie grandeur. On donne les informations suivantes :
- (BD) et (AC) sont perpendiculaires.
- (AD) et (AB) sont perpendiculaires.
- (AB) et (BC) sont perpendiculaires.
- AE = 9,6 cm; CE = 5,4 cm; BC = 9 cm.

 1. Montrer que les droites (AD) et (BC) sont parallèles.
Les droites (AD) et (BC) sont toutes deux perpendiculaires à la même droite (AB),elles sont donc parallèles.
 2. Calculer la longueur AD.
Les triangles ADE et CEB sont semblables.
Relation de Thalès : AE / CE = AD / BC ; 9,6 / 5,4 = AD / 9 ; AD = 9 x9,6 /5,4 =16 cm.
3. Montrer que la longueur BE est de 7,2 cm.
Relation de Pythagore dans le triangle BCE rectangle en E :
BC2 = BE2 +CE2 ; BE2 =92-5,42=51,84 ; BE =7,2 cm.
4. Est-il vrai que l’aire du triangle ABE représente le tiers de l’aire du triangle ABD ?
Aire du triangle ABE : AE x BE / 2 =9,6 x7,2 / 2=34,56 cm2.
AB2 = AC2-BC2 =152-92=144 ; AB = 12 cm.
Aire du triangle ABD : AB x AD /2 = 12 x16 /2=96 cm2.
34,56 / 96 = 0,36 différent de 1/3. L'affirmation est fausse.

Exercice 5 : 21 points.
 Dans cet exercice, les deux parties sont indépendantes.
• Volume du cylindre = Aire de la base × Hauteur du cylindre
 • Aire du disque = p× (rayon)2
• 1 cm3 = 1mL
Pour un anniversaire, on veut préparer des cocktails de jus de fruits.
Partie 1 : Étude des glaçons
Photo du moule à glaçons utilisé et caractéristiques des glaçons :

Chaque glaçon a la forme d’un pavé droit : • de longueur 5 cm; • de largeur 2,5 cm; • de hauteur 1,5 cm.
1. On possède 12 moules à glaçons de ce type. Combien peut-on faire de glaçons en même temps ?
20 x 12 =240 glaçons.
2. Montrer que le volume d’un glaçon est d’environ 19 mL.
Longueur x largeur x hauteur = 5 x2,5 x1,5 =18,75 cm3 ~19 mL.
3. 5 litres d’eau sont-ils suffisants pour remplir ces 12 moules à glaçons ?
Volume d'eau : 240 x18,75 =4 500 mL = 4,5 L.
5 L d'eau sont donc suffisants.

Partie 2 : Le service.
On souhaite servir le cocktail dans des verres cylindriques.

 4. Montrer que le verre a un volume total d’environ 295 mL.
aire de base x hauteur = p R2 x hauteur=3,14 x2,52 x15=294,5 cm3 ~295 mL.
5. Pour verser précisément 25 cL de cocktail, on utilise des verres avec un repère indiquant une contenance de 25 cL.
a. On a préparé 30 litres de cocktail. Combien peut-on remplir de verres contenant 25 cL de cocktail ?
30 L = 3 000 cL ; 3 000 / 25 =120 verres.
b. En versant 25 cL = 250 mL = 250 cm3 de cocktail dans le verre, à quelle hauteur h du verre, le liquide arrive-t-il ? Arrondir au dixième.
250 = p R2 x h ; h = 250 /(p R2) =25 /(3,14 x2,52)~12,7 cm.



  
menu