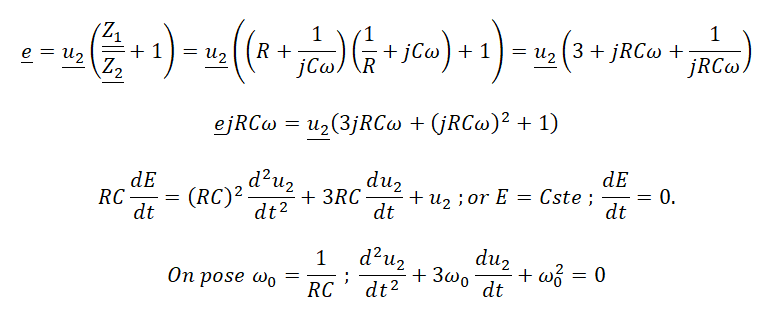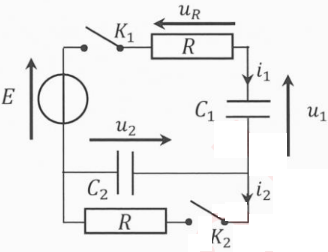
Transitoire d'un double RC, concours Ecole Nationale de l'Aviation Civile 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Les deux interrupteurs sont initialement ouverts, le condensateur C2 est déchargé, C1 est chargé de sorte que la tension à ses bornes soit u1 = ½E. A l'instant t=0, on ferme K1, tout en maintenant K2 ouvert. Pour les 4 premières question, i2(t) = 0 : on retrouve la boucle simple contenant le générateur, la résistance et deux condensateurs en série. 13. Déterminer , à la date t = 0+, la tension uR(0+). Loi des mailles : uR(0+) + u1 = E. Continuité de la tension aux bornes des condensateurs : uR(0+) + ½E = E. uR(0+) = ½E. Réponse B. 14. L'intensité du courant électrique évolue, (lorsdque t >0) selon la loi : i1(t) = A exp(-t / t). Déterminer A et t. Loi des mailles : E = Ri1 +u1 +u2. On dérive : 0 = Rdi1/dt +du1/dt +du2/dt. 0 = Rdi1/dt +i1/C1 +i1/C2 . 0 = Rdi1/dt +i1 /(C1+C2) / (C1C2). di1/dt +i1 /(C1+C2) / (RC1C2)=0. On identifie t = RC1C2 /(C1+C2). A l'instant initial : uR(0+) = ½E =Ri1(0+)=R A ; A = E / (2R). Réponses B et C. 15. Après la fermeture de K1, la tension u1(t) est donnée par la relation : i1 = C1 du1 /dt ; du1 /dt =i1 / C1 =E / (2RC1) exp (-t / t) ; Intégrer : u1(t) = -E t / (2RC1) exp (-t / t) + Cste. u1(t) = -EC2  / (2(C1+C2)) exp (-t / t) + Cste.  u1(t=0+) =½E= -EC2  / (2(C1+C2)) + Cste. Cste = ½E +EC2  / (2(C1+C2)) u1(t) = -EC2  / (2(C1+C2)) exp (-t / t) +EC2  / (2(C1+C2))+½E. u1(t) = EC2  / (2(C1+C2))[1-exp (-t / t)]+½E. Réponse D. 16. Déterminer la tension u2(t) après la fermeture de K1. u2(t) = -E t / (2RC2) exp (-t / t) + Cste. u2(t=0) = -E t / (2RC2) +Cste= 0. Cste = E t / (2RC2). u2(t) = -E t / (2RC2) exp (-t / t) +E t / (2RC2) u2(t) =E t / (2RC2) [1-exp (-t / t)] u1(t) = EC1  / (2(C1+C2))[1-exp (-t / t)] Réponse B. 17. Lorsque le régime permanent est atteint, on ferme K2 tout en laissant K1 fermé à un instant pris comme nouvelle origine des temps. Déterminer à t=0+, l'intensité du courant i2(0+) et déterminer sa valeur lorsque le nouveau régime est établi. A t(0+), la tension aux bornes de la seconde résistance  est égale à la tension u2 en début de régime permanent  soit : u2(t=0+)=EC1  / (2(C1+C2)) ; i2(0+) =EC1  / (2R(C1+C2)) . Lorsque les condensateurs sont chargés : i1(t oo) = i2(t oo) =0. Réponsse A et D 18. On suppose que C1 = C2. Après fermeture de K2, la tension u2(t) évolue selon : d2u2/dt2 +w0 /Q du2/dt +w02u2=0. Déterminer Q. Le circuit est l'association série de deux impédances complexes : Z1 = R +1/jCw) et 1 / Z2 = 1 / R +jCw. Le pont diviseur de tension conduit à : u2 = e Z2 / (Z1+Z2). 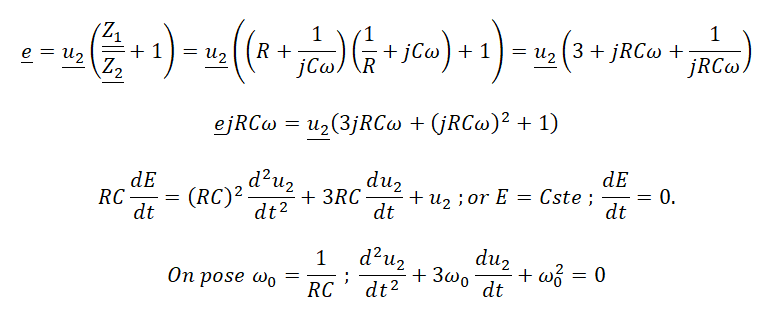Par identification Q = 1 /3. Réponse A.

menu