Physique, lyophilisation, chute dans un liquide, QCM, concours Ecole de Santé des Armées 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. 5 points. La poudre lyophilisée forme une solution ou une suspension après l'ajout d'un liquide. La lyophilisation permet d'éliminer l'eau d'une préparation sans la chauffer. Une fiole de 240 mL contient le liquide à lyophiliser et de l'air à 27 °C sous une pression de 105 Pa. On négligera le volume du liquide face au volume d'air contenu dans le fiole. Etape AB : refroidissement isobare du contenu de +27°C à -40 °C ce qui provoque la solidification de l'eau. Etape BC : on effuctue une baisse de pression isotherme à -40 °C de 105 Pa à 10 Pa ce qui provoque la sublimation de l'eau. 1. Calculer le nombre de mole d'air n0 contenu dans la fiole lors de l'étape AB. P = 105 Pa ; V = 2,40 10-4 m3 ; Température initiale = 273+27=300 K. n0 = PV / (RT) = 105 x2,40 10-4 /(8 x300) =24 /(8 x300) = 3 / 300 = 0,010 mol. 2. Lors de l'étape BC, la baisse de pression isotherme dans la fiole de verre rigide s'obtient par aspiration d'une partie de l'air contenu. Montrer que le nombre de mole d'air restant à l'état C est lié au nombre de mole d'air initial par : nC=nB PC / PA. Evolution isotherme à volume constant : PA V =PBV= nB RT. PC V = nCRT. PC / PA = nC/ nB.  nC=nB PC / PA. 3. On suppose que la préparation liquide à lyophiliser contient au départ 36 g d'eau. a. Calculer le nombre de molécules d'eau contenues dans ce liquide. n = m / M(eau) = 36 / 18 = 2 moles. 2 xNA ~ 2 x 6 1023 =1,2 1024 molécules d'eau. b. Calculer la variation d'énergie interne de l'eau liquide quand elle passe de 27°C à 0°C. DU = m ceau (Tfin - Tini) = 36 x4 (0-27)= -3888 J. c. Indiquer en justifiant, s'il est possible ou non de calculer la variation globale d'énergie interne de l'eau pour la transformation de A vers B. Non, on ne connaît pas l'énergie thermique massique de solidification de l'eau. Exercice 2. 5 points. 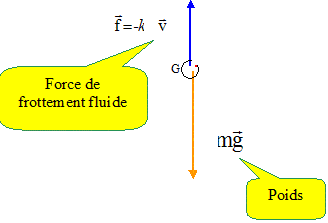On considère une particule solide de masse m en chute verticale dans un liquide à la vitesse V durant laquelle estt n'est soumise qu'à l'action de son poids P et une force de frottement f = k V où k est une constante positive d'unité kg s-1. On se place dans le repère terrestre supposé galiléen et on lui associe un repère unidimensionnel d'axe Oz vertical dirigé vers le haut. La particule sédimente en partant à l'instant t=0 de la surface du liquide avec une vitesse nulle. 1. Exprimer vectoriellement la force de frottement en fonction du vecteur vitesse. 2. Montrer que la vitesse de chute vérifie l'équation dV /dt +k / m V = g .Ecrire la seconde loi de Newton sur un axe vertical orienté vers le bas : mg -kV = mdV/dt. dV/dt +k/m V = g. 3. La solution de cette équation est V(t) = A[1-exp(-Bt] avec A et B des constantes. Proposer des unités pour A et B. B est l'inverse d'un temps  : s-1. A a la dimension d'une vitesse  : m s-1. 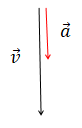4. On donne l'évolution temporelle de la vitesse. a. Représenter sur un axe vertical les vecteurs vitesse et accélération en régime transitoire. La vitesse croît : les vecteurs accélération et vitesse sont colinéaires et de même sens. b. Déterminer graphiquement la constante de temps t du mouvement. 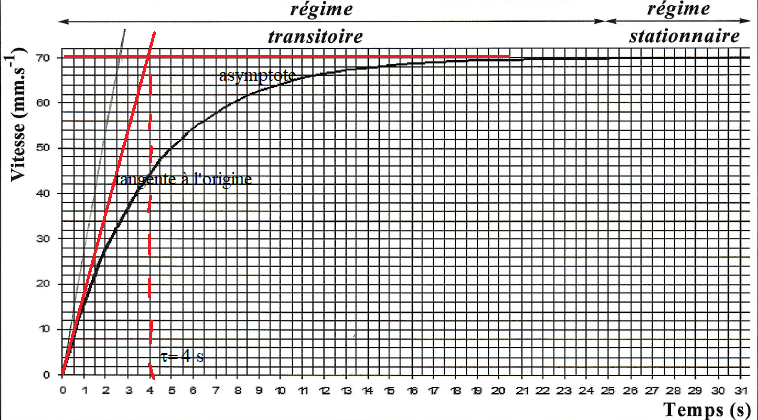Abscisse de l'intersection de l'asymptote avec la tangente à l'origine. On bien abscisse correspondant à 0,63 vlimite = 0,63 x70 =44 m /s c. Montrer que la vitesse limite de chute est Vlim = mg / k. Lorsque la vitesse limite est atteinte, l'accélération est nulle : mg = k Vlim ; Vlim = mg / k. QCM  Partie 1. 4 points. La filtration stérilisante consiste à faire passer le liquide à travers un tamis, trame de fils horizontaux entrecroisés avec une trame de fils verticaux. Cet entrelacement forme des pores carrés de côté "d". On éclaire le tissu avec un faisceau laser de longueur d'onde l = 600 nm et on analyse la lumière reçue sur un écran placé à la distance D =2 m du tissu. On mesure une distance i entre deux franges brillantes consécutives valant environ 12 cm. On rappelle que i = l D / d. 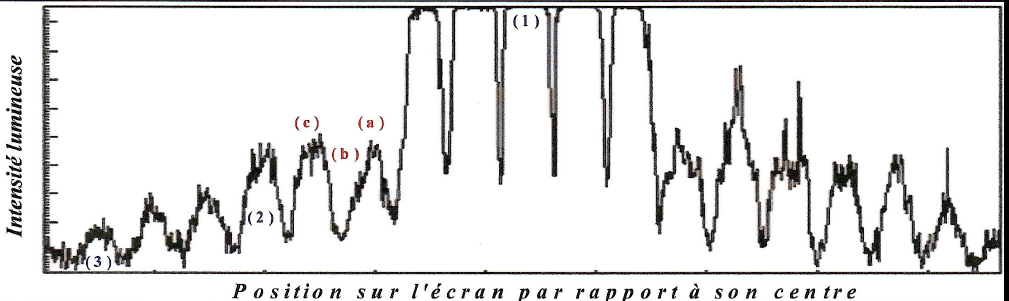QCM 1.  Dans la figure observée sur l'écran : A. La diminution d'intensité lumineuse ( franges 1, 2 , 3) traduit une diffraction. Vrai. B. La diminution d'intensité lumineuse ( franges 1, 2 , 3) traduit une interférence. Faux. C. L'alternance des franges brillante ( a) et sombre (b) traduit une diffraction. Faux. D. L'alternance des franges brillante ( a) et sombre (b) traduit une interférence. Vrai. E. Les items A, B, C et D sont faux. Faux. QCM 2. Sans modifier le milieu de propagation, comment évolue l'interfrange si la fréquence de la lumière éclairant le tamis est multipliée par 2 ? longueur d'onde  = célérité / fréquence. La longueur d'onde sera divisée par deux. i = l D / d. L'interfrange sera divisé par 2. Item D. QCM 3. On donne les tailles de certains micro-organismes : Bactéries : 1 à 3 µm ; champignon : 20 à 100 µm ; levure : 0,3 à 0,02 µm. d = l D / i =600 10-9 x 2 / 0,12 = 12 10-7 /0,12 =10-5 m = 10 µm. Le tamis est adapté pour filtrer uniquement les champignons. Item A. ... .... Partie 2. Un médicament pour la voie pulmonaire est souvent administré en aérosol, dispersion de gouttelettes liquides dans l'air. Cet aérosol peut se former grâce à des ultrasons envoyés dans le liquide. QCM 4.  La formation de gouttelettes apparaît  si la puissance acoustique surfacique en surface du liquide dépasse 10-2 W cm-2. Quel est le niveau d'intensité associé à cette puissance ? I = 102 W m-2. L = 10 log (102 / 10-12) = 10 log (1014 )= 140 dB. Réponse D. QCM 5. L'appreil émet un bruit incommodant de 60 dB ; pour le réduire on entoure le système d'une coque acoustique limitant le bruit en sortie à 40 dB. Combien feut-il d'appareils protégés pour produire un bruit de même niveau qu'un non protégé ? Intensité acoustique d'un appareil non protégé : I1 = 10-12 x 106=10-6 W m-2. Intensité acoustique d'un appareil  protégé : I2 = 10-12 x 104=10-8 W m-2. I1 =100 I2. Réponse B. QCM 6.  Le liquide à transformer en aérosol est introduit dans un nébulisateur au sein d'un réservoir ; pour avoir un aérosol homogène, le réservoir tourne autour d'un axe en même temps qu'il reçoit le faisceau d'US. Le point de remplissage, au bord du réservoir circulaire de rayon R, est animé d'un mouvement circulaire uniforme avec une accélération valant 4 g. Quelle est l'expression  de la durée mise par le point de remplissage pour fair un tour complet ? accélération g = v2 / R. ; v =  (gR) ½. La circonférence 2 pR est parcourue à la vitesse v et T seconde. 2 p R = v T =(gR) ½ T. 2 p R½ =g½ T. T = 2 p (R / g)½. Réponse E. QCM 7. Une gouttelette de masse m sort du masque de l'inhalateur à une vitesse v0 et une hauteur H0 du sol. Quelle est la vitesse avec laquelle la gouttelette touche le sol ? La gouttelette est en chute libre , soumise uniquement à son poids. Théorème de l'énergie cinétique : ½mV2 -½mV02 = mgH0. V2 -V02 = 2gH0 V2  = 2gH0 +V02. V = (2gH0 +V02)½. Réponse A. =

menu