Catapulte
; hydrolyse du bromure de tertiobytyle ; stroboscope ;
concours Geipi Polytech 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1. 12 points.
Dans le cas de l’envoi de petits
satellites dans l’espace,
l’utilisation d’une catapulte comme celle représentée sur
le schéma ci-dessous est à l’étude car elle pourrait
permettre d’économiser de l’énergie par rapport à une
fusée classique.
Dans un tel dispositif, le projectile à lancer (satellite
contenu dans une coque aérodynamique) est d’abord
mis en mouvement dans une chambre d’accélération.
Pour cela, il est fixé à l’extrémité d’un bras rigide de
longueur R= 40 m. Le bras est lui-même mis en
mouvement autour du point C dans un plan vertical
grâce à un moteur électrique.
Le lancer proprement dit peut ensuite s’effectuer
lorsque le projectile a atteint sa vitesse de lancement : au
point L de la trajectoire, à un instant noté tL, le
projectile
est libéré du bras : il est ainsi éjecté verticalement dans le tube
d’éjection.
Cet « élan » lui permet d’atteindre une altitude de plusieurs
dizaines de kilomètres. On s’intéresse au mouvement dans le
référentiel terrestre considéré comme galiléen d’un projectile de
masse M = 50 kg assimilé à un point noté G. La valeur v de la
vitesse du point G dans ce référentiel au cours de son mouvement
jusqu’à l’instant tL est représentée en fonction du temps
sur le
graphique ci-dessous.
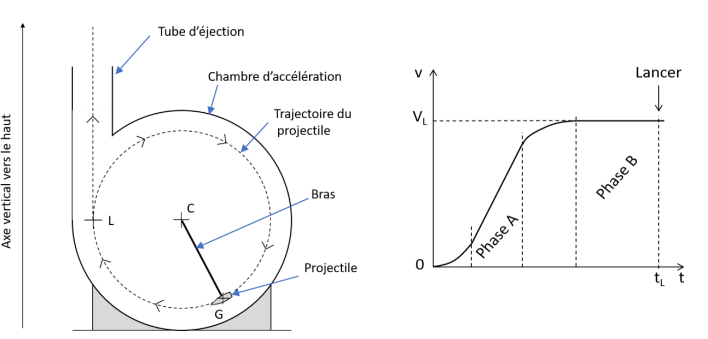
I-1. Comment
qualifier le mouvement du point G au cours de la phase A ?
Le mouvement est circulaire et accéléré.
I-2- Même question pour le mouvement
de G au cours de la phase B.
Le mouvement est circulaire et uniforme.
On étudie le
mouvement de G dans le repère de Frenet au cours de la phase B.
La vitesse du projectile vaut VL=2000 m/s.
Son poids ainsi que les frottements de l’air sont négligés.
I-3- Exprimer
puis calculer les coordonnées at et an du vecteur
accélération a du point G.
at = dv /dt = 0.
an = vL2 / R =20002 / 40 =105
m s-2.
I-4- Ecrire le
principe fondamental de la dynamique appliqué au
projectile. On notera F la résultante des forces extérieures subies par
le
projectile.
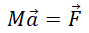
I-5- En déduire
les expressions des coordonnées Ft et Fn de la
résultante F, puis calculer leurs valeurs.
Ft = Mat= 0.
Fn = Man=50 105 = 5 106 N.
I-6- Identifier le ou les systèmes à
l’origine des forces dont la résultante est F ?
Le bras de catapulte.
I-7- Une
force F d’intensité trop élevée engendrerait une détérioration du
dispositif de lancement ; c’est
d’ailleurs le principal problème de ce type de lanceur. Pour diminuer
l’intensité de cette force sans modifier
la valeur de la vitesse de lancement, quel(s) paramètre(s) faudrait-il
modifier ? On précisera pour chaque
paramètre nommé s’il faut augmenter ou diminuer sa valeur pour diminuer
l’intensité de F .
Diminuer la valeur de la masse M ; augmenter la longueur R du bras.
|
...
|
....
|
Exercice
2. 14 points.
L’industrie
utilise de nombreuses réactions impliquant des espèces nucléophiles
pour la fabrication de
réactifs chimiques de base ou lors de synthèses organiques, mises en
œuvre par exemple dans l’élaboration
de médicaments.
La réaction d’hydrolyse du bromure de tertiobutyle : H3C-CBr(CH3)-CH3
, que l’on notera tBuBr en est
un exemple ; son équation-bilan est la suivante :
tBuBr + 2H2O → tBuOH + H3O+ + Br -
La réaction est menée dans un solvant mixte avec un excès d’eau sur une
quantité de dérivé bromé n0
(tBuBr) = 0,050 mol dans un réacteur contenant 500 mL de solution.
II-1- Donner la formule topologique
du produit principal de la réaction : tBuOH et choisir son nom
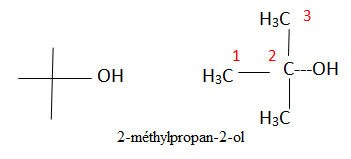
II-2- A
quelle famille de réactions cette réaction appartient-elle ?
Réaction de substitution.
L’évolution du système est suivie par conductimétrie, ce qui permet
d’établir et de suivre la variation de la
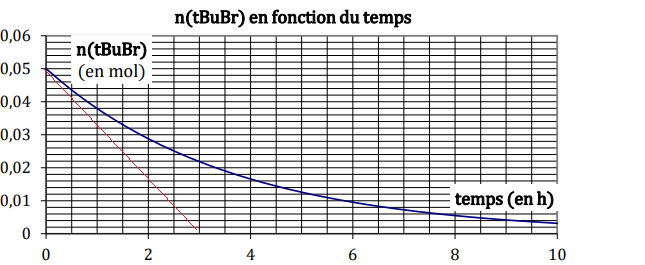
quantité de bromure de tertiobutyle n(tBuBr) en fonction du temps.
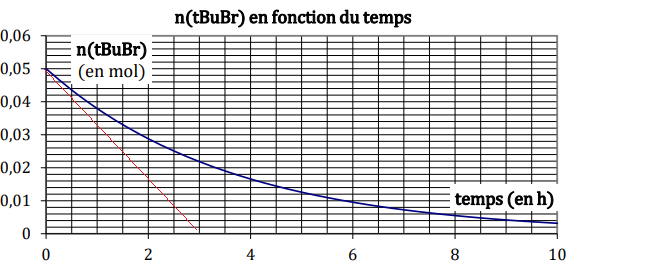
II-3- Choisir parmi
les courbes représentant l’évolution de s en fonction du temps celle
dont l’allure
correspond au suivi conductimétrique de la réaction.
Les ions H3O+ et Br -formés lors de
l'hydrolyse contribuent à la conductivité de la solution : la
conductivité de la solution augmente puis devient constante en fin de
réaction.
II-4- On note t½
le temps de demi-réaction. En considérant que la réaction est totale,
compléter le
tableau d’avancement.
temps
( heure)
|
0
|
t½
|
temps
infini |
(tBuBr]
mol / L
|
0,1
|
0,05
|
0
|
[tBuOH]
mol /L
|
0
|
0,05
|
0,1
|
Vitesse
volumique ( mol L-1 h-1)
|
0,017
pente de la tangente à l'origine
|
XXX
|
0
|
.
L’étude expérimentale montre que la réaction suit une loi de vitesse
d’ordre 1 et correspond à un mécanisme
en trois actes élémentaires.
II-5- Citer parmi
les espèces impliquées dans le mécanisme celles constituant un
intermédiaire réactionnel.
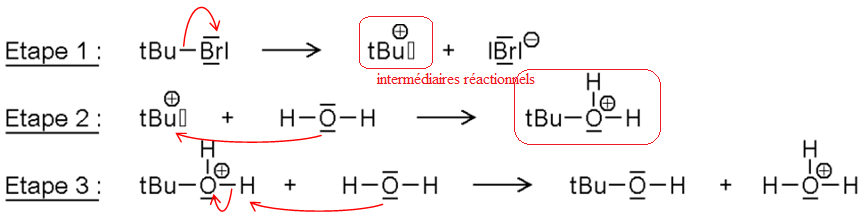
II-6- Compléter le
mécanisme réactionnel en représentant pour chaque étape la ou les
flèche(s) courbe(s)
décrivant les mouvements de doublets électroniques.
II-7- Sachant qu’il
s’agit d’une réaction du premier ordre, on peut établir la relation
suivante entre la
constante de vitesse et le temps de demi-réaction : t½ = ln2 / k.
Choisir la constante de vitesse k correcte
parmi les propositions du document réponses. NB : On rappelle que ln2 ~
0,693.
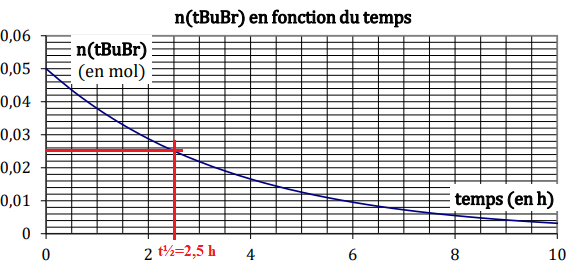
k = 0,693 /2,5 ~0,277 h-1.
II-8-
Exprimer la loi de vitesse de la réaction.
v = k [tBuBr].
Exercice III. Stroboscope
14 points.
Un stroboscope est une lampe qui émet à intervalles réguliers des flashs lumineux de courte durée. Son
principe de fonctionnement repose sur la répétition du cycle de charge et décharge d’un condensateur selon
le circuit électrique présenté sur la figure ci-dessous.
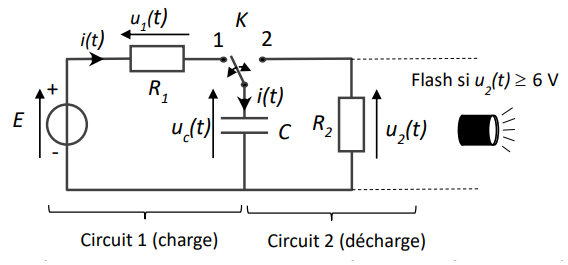
Le circuit 1 de charge (K en position 1) est constitué d’une source idéale de tension continue E = 10 V montée
en série avec un dipôle ohmique de résistance R1 = 60 ohms et un condensateur plan de capacité C = 5,0 x 10-4
F. Le circuit de décharge (K en position 2) est constitué du condensateur en série avec la lampe flash que l’on
assimile à un dipôle ohmique de résistance R2. Dans ces conditions, on souhaite déterminer les principales
caractéristiques du stroboscope à savoir, la fréquence f d’apparition des flashs lumineux successifs et la durée Dt d’illumination de la lampe pendant un flash lumineux.
Partie préalable : Modèle électrique de la résistance et du condensateur
I.1 Donner l’expression littérale reliant la tension u1(t) aux bornes de R1 et le courant i(t) la traversant.
u1(t) =R1 i(t).
I.2 Choisir sur le document réponses l’expression littérale reliant la tension uc(t) aux bornes de C et le courant
i(t) le traversant. On pourra s’appuyer sur l’unité de la capacité C du condensateur, le farad (1 F = 1 A s V-1)
.
i(t) = dq(t) /dt et q(t) = C uc(t) ;
i(t) =C d uc(t)/dt.
Partie 1 : Phase de charge du condensateur.
Le condensateur étant initialement déchargé, le commutateur
bascule en position 1 à l’instant t = 0.
I.3 L’équation différentielle vérifiée par la tension uc(t) lors de la charge du condensateur peut s’écrire sous la forme :
duc(t)/dt + a uc(t) = b.
Donner les expressions littérales de a et b en fonction des grandeurs électriques qui vous
semblent pertinentes.
Additivité des tensions : E = R1 i(t) + uc(t).
i(t) =C d uc(t)/dt.
E = R1C d u(t) / dt+ uc(t).
d u(t) / dt+ 1 / (R1C)uc(t) = E /(R1C).
On identifie : a = 1 / (R1C) ; b = E /(R1C).
I.4 A l’aide de la condition initiale, choisir sur le document réponse l’expression littérale de uc(t), solution de
cette équation différentielle.
uc(t) = 0, condensateur déchargé.
uc(t) = E(1-exp(-t / (R1C)).
I.5 Donner l’expression littérale du temps caractéristique t1 du circuit de charge du condensateur en fonction
de C et R1 puis calculer sa valeur numérique (en ms).
t1 =R1C = 60 x 5 10-4 =0,03 s = 30 ms.
I.6 En déduire l’expression littérale et la valeur numérique du temps tfin (en ms) à partir duquel on peut
considérer que le condensateur est totalement chargé.
tfin ~5t1 = 150 ms.
I.7 Parmi les courbes présentées sur le chronogramme ci-dessous, choisir celle dont l’évolution correspond
aux variations de la tension uc(t) aux bornes du condensateur lors de sa charge complète.
uc(t½) = E(1-exp(-1))~0,63 E ~6,3 V.

Partie 2 : Phase de décharge du condensateur.
K bascule en position 2 à l’instant t = 150 ms. L’évolution de
la tension uc(t) aux bornes du condensateur lors de sa décharge est donnée.
I.8 En utilisant la méthode de votre choix, déterminer la valeur du temps caractéristique t2 lors de la décharge
du condensateur (en ms).
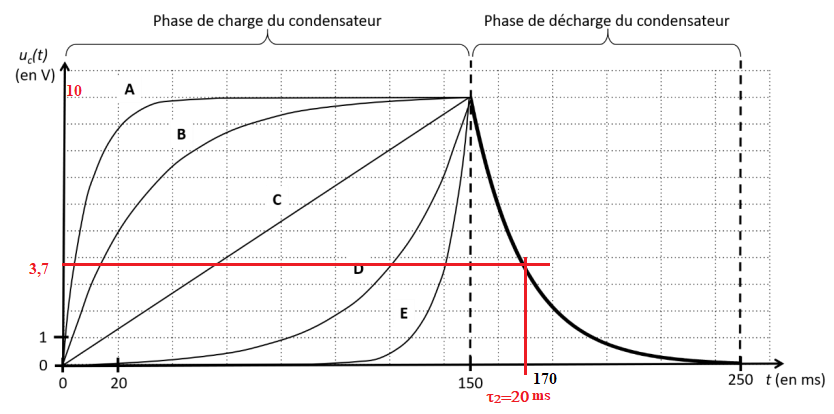
I.9 Donner l’expression littérale de la résistance R2 et calculer sa valeur numérique.
R2 = t2 / C =0,020 / (5 10-4)= 40 ohms.
I.10 En sachant que la lampe flash se déclenche dès que la tension aux bornes de R2 dépasse 6 V, et qu’elle
reste allumée tant que cette tension reste supérieure à 6 V, déterminer la durée Dt d’illumination de la lampe
pendant un flash (en ms).
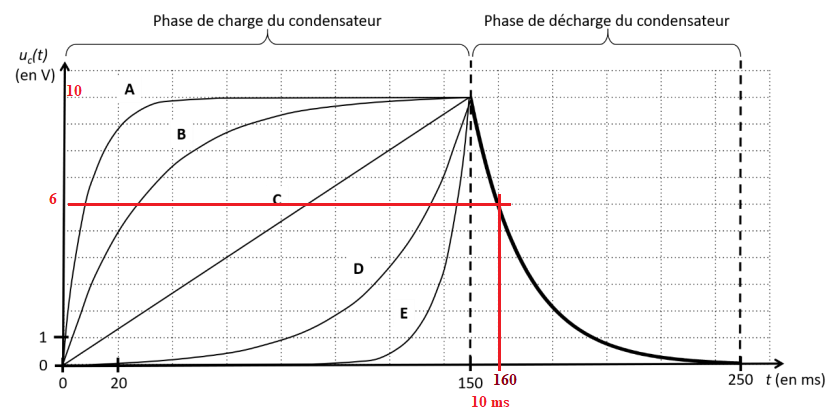
|
|
=
|
|