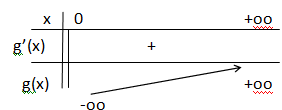
Mathématiques : spécialité ; concours Geipi Polytech 2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1.14 points Partie A On considère la fonction g définie pour tout réel x strictement positif par g(x) = 2x3 + ln(x) − 2.  I-1- Compléter le tableau des variations de la fonction g en faisant apparaître les limites en 0 et en +oo. Aucune justification n’est attendue. g'(x) = 6x2+1/x > 0 sur ]0 ; +oo[.   I-2- Justifier que l’équation 𝑔(𝑥) = 0 admet une solution unique. On note a cette solution. g(x) est continue et strictement croissante sur ]0 ; +oo[ de -oo à +oo. D'après le corollaire du théorème des valeurs intermédiaires, l'équation g(x) =0 admet une unique solution.  I-3- Compléter le tableau de signe de la fonction g. Partie B. On considère la fonction f définie pour tout réel x strictement positif par f(x) =( x3+1−ln(x)) / x .  I-4- Pour tout x > 0, exprimer f '(x) en fonction de g(x), où g est la fonction de la première partie. Détailler le calcul. On pose u = x3+1-ln(x) et v = x. u' = 3x2-1/x =(3x3-1) /x ; v' = 1 /x. (u'v-v'u) / v2 =[3x3-1-x3-1+ln(x)] / x2=g(x) / x2.  I-5-a- Déterminer la limite de f(x) quand x tend vers zéro. Justifier la réponse. x3+1−ln(x) tend vers +oo et x tend vers zéro :  f(x) tend vers +oo. I-5-b- Déterminer la limite de f(x) quand x tend vers +oo. Justifier la réponse. (x3+1) / x tend vers +oo. Par croissance comparée, ln(x) / x tend vers zéro. Par somme des limites, f(x) tend vers +oo. 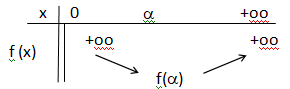I-6- Compléter le tableau des variations de la fonction f, en faisant apparaître les réels a, f(a) et les limites obtenues. Exercice II (14 points). L’espace est rapporté à un repère orthonormé (𝑂, 𝑖 ,𝑗 , 𝑘 ). On considère les points A, B et C de coordonnées respectives : A(1 ; 2 ; 3), B(−3 ; 0 ; 1) et C(0 ; 0 ; 4).  Partie A – Questions préliminaires II-1- Donner les coordonnées des vecteurs :  . 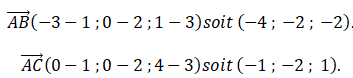II-2- Calculer AB. Détailler le calcul. AB2 =(-4)2 +(-2)2 +(-2)2 =24 ; AB = 24½ =2 x6½.  Partie B – II- 3-a- Justifier que les points A, B et C ne sont pas alignés. 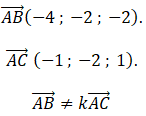II-3-b- Vérifier qu’une équation cartésienne du plan (ABC) est x – y – z + 4 = 0  xA – yA – zA + 4 =1-2-3+4=0 est vérifié; A appartient à ce plan.  xB – yB – zB + 4 =-3-0-1+4=0 est vérifié; B appartient à ce plan.  xC – yC – zC + 4 =0-0-4+4=0 est vérifié; C appartient à ce plan. . II-4-a- Donner les coordonnées du point I milieu du segment [𝐴𝐵]. xI = (xA+xB) / 2 =(1-3) / 2 = -1 ; yI = (yA+yB) / 2 =(2+0) / 2 =1 ; zI = (zA+zB) / 2 =(3+1) / 2 = 2.  II-4-b- En déduire une équation cartésienne du plan P passant par I et orthogonal à la droite (AB). Justifier la réponse. Le plan  estorthogonal à la droite (AB): -4x-2y-2z+d=0. I(-1 ; 1 ; 2) appartient à ce plan : -4 x(-1) -2 x1 -2 x2+d=0 ; d =2.  -4x-2y-2z+2=0. ou bien : 2x+y+z-1=0.  II-5-a- Justifier que les plans P et (𝐴𝐵𝐶) sont sécants selon une droite D. Les vecteurs normaux des plans (P) et (ABC) n'étant pas colinéaires, les deux plans sont sécants selon une droite D. II-5-b- Donner un système d’équations paramétriques de la droite D. Aucune justification n’est attendue. Equation du plan (ABC) est x – y – z + 4 = 0. Equation du plan P : 2x+y+z-1=0. x= -1 ; y = t ; -1-t-z+4=0 soit z = 3-t avec t réel.  On considère la sphère S de centre I et de diamètre [AB].  II-6-a- Donner une équation cartésienne de S. Aucune justification n’est attendue. (x-xI)2 +(y-yI)2 +(z-zI)2 = AB2 /4. (x+1)2 +(y-1)2 +(z-2)2 =24/4=6.  II-6-b- Justifier que le point 𝐶 appartient à S. (xC+1)2 +(yC-1)2 +(zC-2)2 =1+1+22=6.  II-6-c- Justifier que le triangle ABC est rectangle en C. ... .... 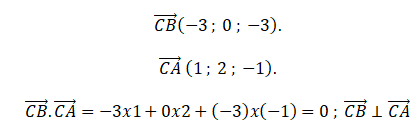Exercice III. On dispose de 100 dés dont 25 sont pipés. Pour chaque dé pipé, la probabilité d’obtenir le chiffre 6 lors d’un lancer est égale à 0,5 . Pour chaque dé non pipé, la probabilité d’obtenir le chiffre 6 lors d’un lancer est égale à 1 / 6 .  Partie A – Un seul lancer.  Dans cette partie, on donnera les résultats sous la forme d’une fraction irréductible. On tire un dé au hasard parmi les 100 dés et on lance ce dé. On note T l’événement : « le dé choisi est pipé » et A1 l’événement : « on obtient un 6 lors du lancer »  III-1- Donner P(T), P(non T), PT(A1) et PnonT(A1). P(T) =25 / 100 = 0,25. P(non T) = 1-P(T) = 0,75. PT(A1) = P(T n A1) / P(T) =0,25 x0,5 / 0,25=0,5. PnonT(A1)=1 /6.  III-2- Calculer P(A1). Justifier et détailler le calcul. Formule des probabilités totales : P(A1) =P(T n A1) + P(non T n A1) =0,5 x0,25 +0,75 x1 / 6 = 0,125 +0,125 = 0,25.  III-3- Calculer PA1 (T). Justifier et détailler le calcul. PA1 (T) = P(T n A1) / P(A1 )=0,25 x0,5 / 0,25 =0,5. Partie B – n lancers indépendants.  Dans cette partie, n est un entier naturel non nul. On choisit un dé au hasard parmi les 100 dés puis on le lance n fois. On considère que les n lancers sont indépendants. On note An l’événement : « on n’obtient que des 6 lors des n lancers ».  III-4- Exprimer PT(An), Pnon T(An) et P(An) en fonction de n. Aucune justification n’est attendue. PT(An)= 0,5n. Pnon T(An)= (1/6)n. P(An)=0,25 x 0,5n +0,75 x(1/6)n. III-5- Déterminer la valeur du nombre réel a > 1 tel que PAn(T) = an /(an+3) . Aucune justification n’est attendue. PAn(T) =3n/(3n+3)= = an /(an+3) soit a = 3.  III-6- En déduire la limite de  PAn(T)  quand n tend vers +oo. Justifier la réponse. PAn(T) =3n/(3n+3) = 1 / (1+3 / 3n). Quand n tend vers plus l'infini : 3/3n tend vers zéro et PAn(T) tend vers 1. =

menu