Addition
sur une parabole, concours général
mathématiques 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Le
plan est muni d’un repère orthonormé.
. Pour tout point M du plan, on note (xM ; yM) ses coordonnées.
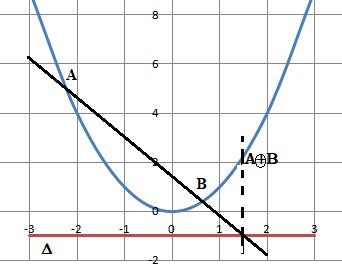
Soient P la parabole d’équation y = x2 et D la droite d’équation y =−1.
Pour tous points A et B de P tels que yA différent de yB, on note A⊕B le point de P
dont l’abscisse est celle du point d’intersection des droites (AB) et D.
Partie 1 : propriétés de ⊕.
1. Soient A et B deux points de P tels que yA différent de yB. Exprimer xA⊕B en
fonction de xA et xB.
Coefficient directeur de la droite (AB) : (yA-yB) / (xA-xB)= (xA2-xB2) / (xA-xB)= xA+xB.
Equation de la droite (AB) : y =(xA+xB) x+constante.
yA=xA2 = (xA+xB) xA+constante.
constante = -xAxB.
y =(xA+xB) x-xAxB.
-1=(xA+xB) xA⊕B-xAxB.
xA⊕B = (xA xB -1) / (xA+xB).
2. Soient A, B et C trois points de P. On suppose que :
yA diffère de yB, , yA⊕A diffère de yB , yA diffère de yA⊕B.
Démontrer que les points (A⊕B)⊕C et A⊕(B ⊕C) sont confondus.
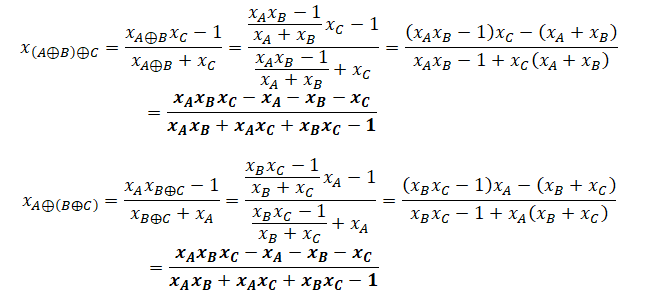
Les points(A⊕B)⊕C et A⊕(B ⊕C) ont même abscisse et sont sur la parabole : ils sont donc confondus.
|
...
|
....
|
Pour tout point A de P distinct du point O (de coordonnées (0;0)), on
note A⊕A le point de P dont l’abscisse est celle du point d’intersection de la tangente à
P en A et de D.
3. Soit A un point de P distinct de O.
a. Exprimer xA⊕A en fonction de xA.
Coefficient directeur de la tangente en A : 2 xA.
Equation de la tangente en A : y = 2 xA x+ constante.
yA=xA2 =2 xA xA +constante ;
constante = -xA2 .
y = 2 xA x-xA2 .
-1 =2 xA x-xA2 .
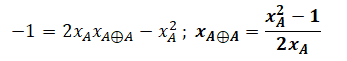
b. Soit B un point de P tel que :
yA⊕A diffère de yB, yA difère de yB, yA diffère de yA⊕B.
Démontrer que les points (A⊕ A)⊕B et A⊕(A⊕B) sont confondus.
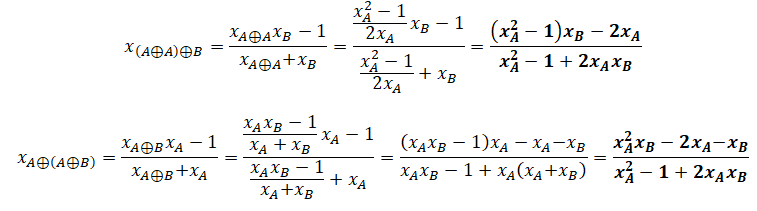
Les points (A⊕ A)⊕B et A⊕(A⊕B) ont même abscisse et sont sur la parabole : ils sont donc confondus.
|
|
=
|
|