Etude
d'une suite de points, concours général
mathématiques 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Soit A un point dela parabole P d'équation y = x2. On lui assocte une suite de points (An) définie par A0 = A et la
relation de récurrence :
pour tout entier n >0, An+1 =An⊕An si An diffère de zéro , sinon 0.
Pour alléger les notations, on pose xn = xAn .
4. On suppose, dans cette question, que A est le point de coordonnées (3 ; 9).
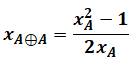
a. Démontrer que, pour tout n dans N, on a xn différent de 0.
x0 =3 ; xn+1=(xn2-1) / (2xn).
Démonstration par récurrence :
Initialisation : la relation est vraie au rang zéro.
Hérédité : xn appartient à Q* moins les valeurs -1 et 1.
xn diffère de 1, donc xn2-1 diffère de zéro. Par conséquence xn+1 diffère de zéro.
xn+1=1 conduit à : xn2-1 = 2 xn ; xn2- 2 xn -1=0.
Déterminant D = 4+4=8.
x1 = (2+8½) / 2 = 1+2½ ; x2 = 1-2½.
x1 et x2 n'appartiennent pas à Q, donc xn+1 diffère de 1.
b. Démontrer que la suite (xn) ne converge pas.
On suppose que (xn) converge vers l réel.
xn+1=(xn2-1) / (2xn).
l = (l2-1) / (2l) ; 2l2=l2-1 ; l2= -1. Impossible.
Donc la suite (xn) ne converge pas.
On rappelle que, pour tout x dans Q∗, il existe un unique couple d’entiers (a,b) tels que :
b >1, PGCD(a,b)= 1 et x =a / b.
. On note alors H(x) le plus grand des entiers |a| et |b|, soit
H(x)=max{|a|, |b|}.
Par exemple H(-4 /3) = 4
On convient de plus que H(0) =1.
Pour tout point P de la parabole P, tel que xp appartient à Q, on pose h(P)= ln(H(xp)).
5. Démontrer que, pour tout c dans N∗, l’ensemble E(c) ={P appartenant à la parabole, xp appartient à Q et h(P)< c} est fini.
h(P)< c entraîne ln(H(xp)) < c ; H(xp)) < ec.
xp = a / b ; max(|a|, |b|) < ec.
Donc |a|) < ec; |b|) < ec.
Le nombre de parabole est fini pour a et pour b.
Le nombre de parabole est fini pour a / b.
6. Soit (a,b) appartenant à Z∗×N∗. Démontrer que, si PGCD (a,b)=1, alors
PGCD (a2−b2,ab)= 1.
Soit PGCD(a, b) = 1.
On suppose que PGCD(a2−b2,ab)= k avec k diffèrent de 1 soit k > 2.
k possède donc un diviseur premier que l'on note p.
D'après le lemme d'Euclide : si p divise le produit ab, alors p divise a ou p divise b.
Premier cas : p divise a : p divise a, donc p divise a2.
or p divise a2-b2 ainsi que a2 : par conséquent p divise b2 ; donc p divise b.
Impossible p ne peut pas diviser a et b.
Second cas : p divise b : donc p divise b2.
or p divise a2-b2 ainsi que b2 : par conséquent p divise a2 ; donc p divise a.
Impossible p ne peut pas diviser a et b.
Par conséquent :
PGCD (a2−b2,ab)= 1.
7. Démontrer qu’il existe deux réels m et M tels que pour tout point P de la parabole tel que xp appartient à Q∗, on a
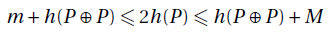
8. Soit (un) une suite réelle. On pose
v0 = 0 et, pour tout n >1, 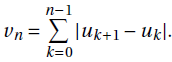
On suppose que la suite (vn) est majorée et on souhaite démontrer que la suite (un) converge :
a. Démontrer que la suite (vn) converge.
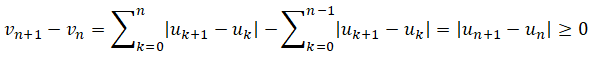
La suite (vn) est croissante et majorée, donc elle converge.
b. Démontrer que pour tout entier naturel n, on a
0< un+1−un +|un+1 −un|<2|un+1 −un|.
-|un+1−un|< un+1 −un < |un+1 −un|.
Quelque soit (a, b) apparternant à R2 : a-b < |a-b|
Si a-b > 0 alors a-b < |a-b|.
Si a-b < 0 alors a-b < |a-b|.
-|a-b| < a-b <|a-b|.
On pose a = un+1 et b = un :
-|un+1-un| < un+1-un <|un+1-un|.
Soit :
0< un+1−un +|un+1 −un|<2|un+1 −un|.
c. En déduire que la suite (un +vn) converge.
Pour k entier appartenant à [0 ; n-1] :
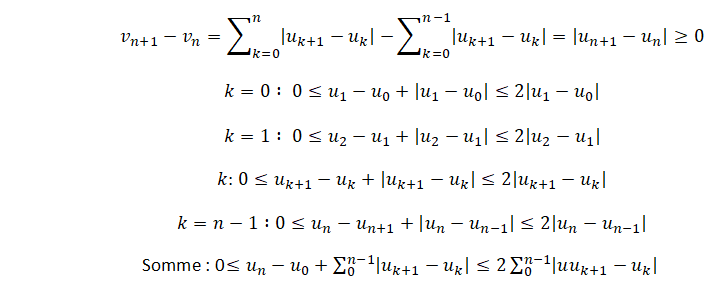
Donc quelque soit n entier naturel : 0 < un-u0 +vn < 2 vn.
u0 < un +vn < u0+2 vn.
(vn) est croissante et converge vers une limite notée l.
Donc pour tout entier naturel n : u0 < un +vn < u0+2 l.
un +vn est donc bornée.
un+1+vn+1-(un+vn)=(un+1-un) +(vn+1-vn).
Or vn+1-vn =|un+1-un|
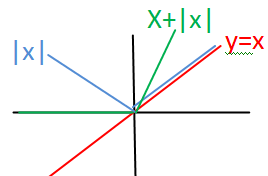
(un+1-un) +|un+1-un| > 0. Donc la suite (un +vn) est croissante.
De plus elle est bornée, donc elle converge.
d. Conclure.
La suite (vn) converge ; la suite (vn+un) converge.
Soustraire : la suite (un) converge.
|
...
|
....
|
9. Soit à nouveau le point A de coordonnées (3 ; 9) et soit (An) la suite récurrente associée à A. Pour tout entier naturel n, on pose tn = h(An) / 2n . Démontrer que la suite (tn) converge.
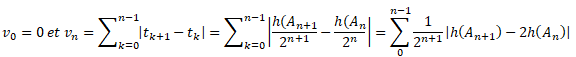
D'après la question 7 : m < 2h(An)-h(An+1) < max(m, M).
Donc :
2h(An)-h(An+1) < M
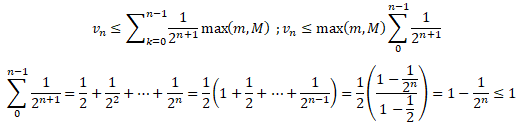
vn < max(m, M) : la suite (vn) est majorée.
D'après la question 8, la suite (tn) converge.
|
|
=
|
|