Fonctions,
concours général
mathématiques 2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
On dit qu'une fonction vérifie la propriété E si, pour tout réel x :
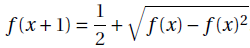
1. Proposer une fonction continue qui vérifie la propriété E .
Hypothèse : il existe une fonction constante f(x) = k ( k réel) vérifiant cette propriété.
k-k2 doit être positif ou nul ; k(k-1) > 0 ; k appartient donc à [0 ; 1].
k =½ +(k -k2)½ ; k-½ =(k -k2)½ ; (k-½)2 = k-k2.
k2-k+0,25=k-k2.
2k2-2k+0,25=0.
Discriminant D = 4-2=2.
k1= (2+2½) / 4 ; k1= (2-2½) / 4 ;
Ces deux solutions appartiennent à [0 ; 1].
Par contre f(x) > ½ et k1 < ½ : donc k1 ne convient pas.
2. On rappelle qu’une fonction g définie sur R est périodique s’il existe un réel T > 0
tel que pour tout réel x, g(x +T ) = g(x).
Soit f une fonction vérifiant E . Démontrer que f est périodique.
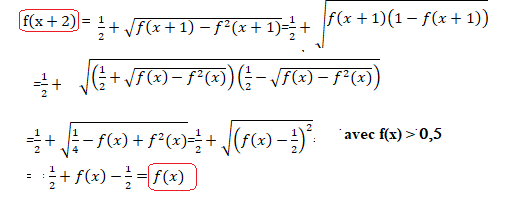
3. Proposer une infinité de fonctions continues f vérifiant E et f (0) =0,5.
f(x)=sin(px) est 2p périodique .
f(x) = ½|sin(px)| +½ est 2p périodique et f(0) = ½.
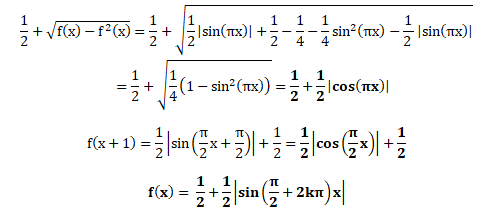
.
|