Aide
auditive; microscope.
Concours ITPE 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Aide
auditive.
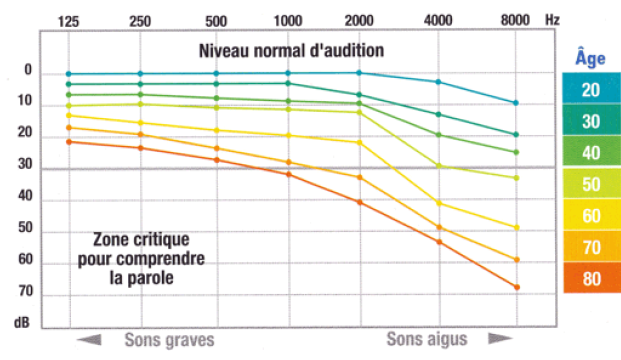
Le
vieillissement est responsable d'une perte de sensibilité aux sons
aigus. Pour corriger ce problème, on réalise un système amplifiant les
hautes dréquences.
On considère le flitre CR suivant :
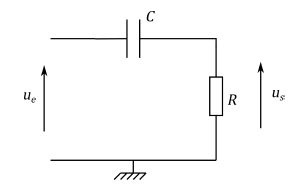
1. Déterminer la nature du filtre.
En
très basses fréquences, le condensateur se comporte comme un
interrupteur ouvert : la tension de sortie us est nulle.
En
hautes fréquences le condensateur est équivalent à un
interrupteur fermé : la tension de sortie estégale à ue.
Le
circuit est donc un filtre passe haut.
2.
Montrer que la fonction de transfert se met sous la forme H = j x /(1+jx) avec x = w / w0.
H= us/ue.
us
= R i ; Z = R+1/(jCw) =(jRCw+1) / (jCw) ; i = ue / Z=ue (jCw)
/ (jRCw+1).
us
= Rue (jCw)
/ (jRCw+1).
us
/ue =R(jCw)
/ (jRCw+1).
On pose w0
= 1 / (RC).
H =jw / w0 / (1+jw
/ w0).
On pose x = w / w0.
H
= j x /(1+jx)
3. Montrer que w0 est la pulsation de coupure à
-3 dB de ce filtre. Donner l'ordre de grandeur de w0.
Si R = 1,0 104 ohms, en déduire C.
Module de H : H = jx(1-jx) / (1+x2)=(jx+x2)
/ (1+x2).
H =(x2+x4)½
/ (1+x2)=x
/(1+x2)½.
Gain G = 20 log H =20 log[x /(1+x2)½].
Pulsation de coupure à -3 dB : -3=20 log[x /(1+x2)½].
-3/20= -0,15 =log[x /(1+x2)½].
10-0,15 ~0,708= x /(1+x2)½;
0,5 ~x2 /(1+x2) ; x ~ 1 ; wcoupure ~w0.
4. Tracer le diagramme de Bode en
gain.
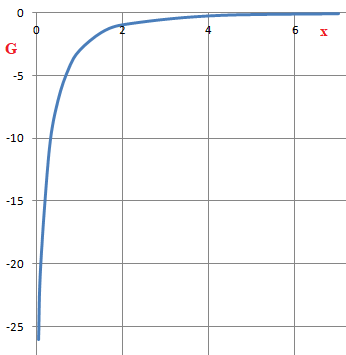
5. Ce filtre est-il
adapté à la réalisation d'une aide auditive ?
Pour les plus de 70 - 80 ans, la zone critique correspond aux
fréquences supérieures à environ 1000 Hz.
w
= 2 pf = 2 *3,14
*1000 ~6,3 103 rad/s.
On utilise la structure suivante : R2 = 1 kW.
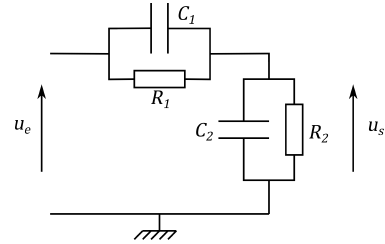
6. Ecrire
la fonction de transfert H=
us
/ ue sous
la forme :
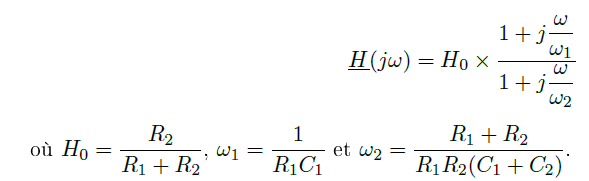
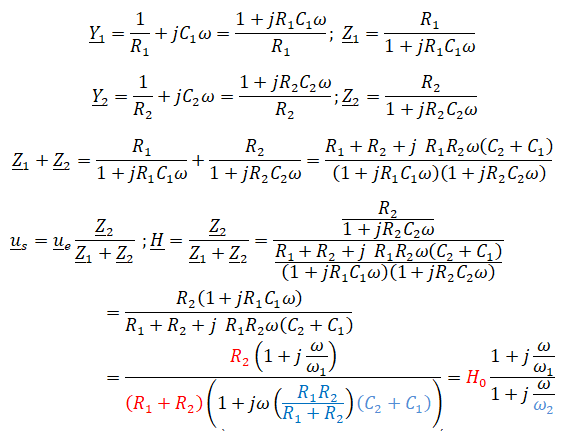
7. On donne le
diagramme de Bode en gain. Justifier son allure. Comment choisir w1 et w2 pour avoir GHF
> GBF ?
G = 20 log (H).
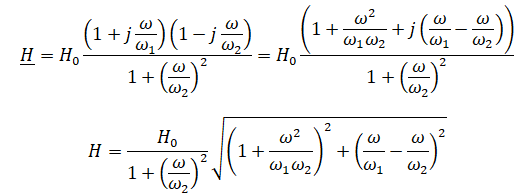
8. Déterminer graphiquement w1 et w2 .
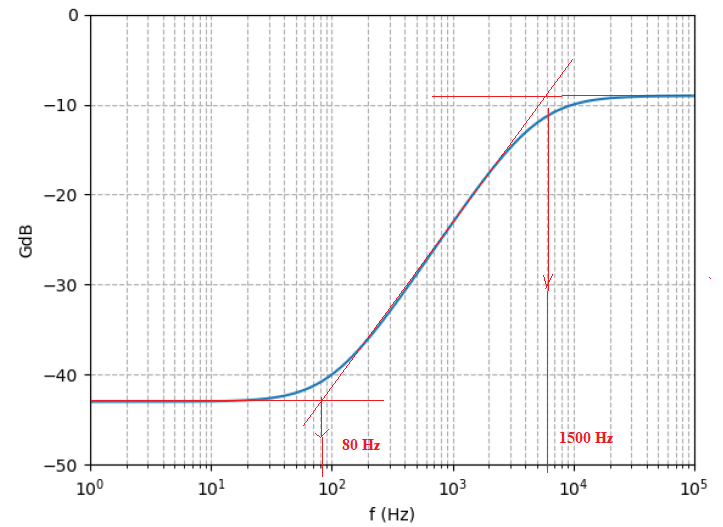
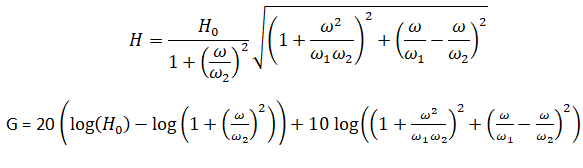
9. En
déduire R1, C1 et C2.
w tend
vers zéro ; G tend vers -43 dB.
20 log H0 = -43 ; H0 ~0,007= R2/(R1+R2)=1/(R1+1)
;
R1+1=1/0,007 ~141. R1 = 140 kW.
w1=2
x3,14 x80~500 rad/s.
1/(R1C1)=500 ; C1 =1/(500 x1,4 105)~1,4
10-8 F.
w2=2
x3,14 x1500~9,4 103 rad/s.
(R1+R2) / (R1R2(C1+C2)
=1,41 105 /(1,4 108(1,4 10-8 +C2))
=1,0 10-3 /(1,4 10-8 +C2)=9,4
103.
1,4 10-8 +C2=1,0 10-3 /(9,4 103)=1,1 10-7 ; C2=9,3
10-8 F.
|
...
|
....
|
II. Microscope.
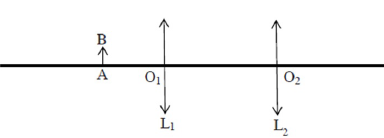
O1O2=D=120 mm. f '1 = 5 mm ; f '2
= 15 mm.
10. Rappeler les conditions de Gauss.
Les rayons lumineux sont peu inclinés sur l'axe optique et en sont très
proche. Rayons paraxiaux.
11. On définit
l'intervalle optique D
= mesure algébrique ( F'1 F'2). l'exprimer en
fonction de f '1 et f '2.
D=D-f '1-f
'2=120-5-15=100 mm.
12. L'objet est
placé à la distance d de L1. L'image intermédiaire se trouve
dans le plan focal objet de L2.
a. Exprimer d en fonction de f '1
et D. Faire
l'application numérique.
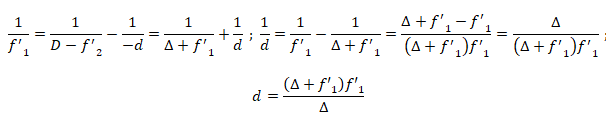
d = (100 +5) x5 / 100 =5,25 mm.
b. Exprimer le
grandissement g1
créé par l'objectif en fonction de f '1
et D. Faire
l'application numérique.
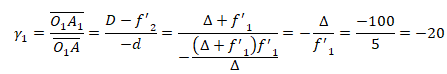
c. Quel est l'intérêt de placer
l'objet à cet endroit ?
L'image définitive est à l'infini ; l'oeil observe sans fatigue.
d. Faire un schéma.
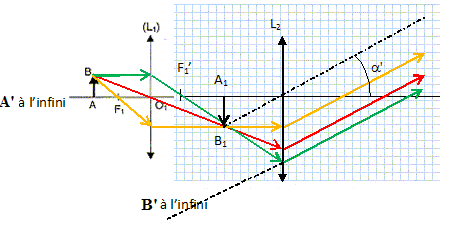
13. Grossissement G = |a' / a|. a angle sous lequel l'objet
est vu à l'oeil nu, l'oeil étant à d = 250 mm.
Exprimer G en fonction de D,
f '1 et f '2. Faire l'application.
tan a ~ a =AB/ d
=AB/ 0,25=4 AB.
tan a' ~ a'=A1B1/
f '2 ;
A1B1/ AB =F'1A1
/ O1F'1 = F'1F2 / O1F'1
= D / f '1
; A1B1= AB D
/ f '1.
a'=AB D
/ (f '1 f '2).
G = D
/ (4f '1 f '2)=0,100 /(4x0,005x0,015)~333.
14. On utilise ce
microscope pour mesurer l'épaisseur e d'une lame de verre à faces
parallèles d'indice n = 1,6. On colle une pastille violette sur sa face
gauche et une pastille rouge sur sa face droite.
On
fait la mise au points sur la pastille rouge, puis on déplace la
lunette d'une distance h à l'aide d'une vis micrométrique pour faire la
mise au point
sur la pastille violette.
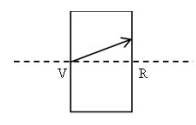
On
considère le rayon issu de V qui se dirige vers la face droite de la
lame, où il subit une réfraction. Le rayon réfracté ou son prolongement
coupe l'axe en un point V'. Reproduire le schéma en indiquant la
position de V'.
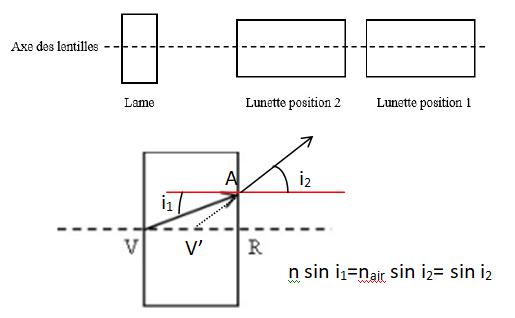
Quelle est la distance V'R en fonction de n et de l'épaisseur e de la
lame ?
tan i1=AR / VR =AR / e ; tan i2= AR /
V'R.
tan i1 / tan i2=V'R / e.
Pour les petits angles : tan i ~sin i :
tan i1 / tan i2~ sin i1 /sin i2~1
/n.
V'R ~e /n= e / 1,6.
La figure montre la vis micrométrique lors des positins 1 et 2.

Déterminer la valeur mesurée de h en mm puis déterminer e.
h = 40,70-40,30=0,40 mm=4 10-4 m.
h = e-V'R =e-e/1,6 =0,375 e ; e = 4 10-4 /0,375= 1,07 10-3
m = 1,07 mm. |
|
|
|