Suspensions d'un véhicule. Concours ITPE 2024.

Suspensions à ressort.
L'extrémité inférieure du ressort est reliée à une roue qui reste au contact avec le sol. L'extrémité supérieure est en contact avec le véhicule.
A une fonction x(t) = X_m cos(wt+f) on associe x(t) = X_m exp(iwt) avec X_m = x_m exp(if).
Masse du véhicule à vide m =1000 kg.
Constante de raideur du ressort de la suspension k = 1 10⁵ Nm^-1 ; longueur au repos l₀.
On néglige pour l'instant tout amortissement.
Position initiale de la masse z_e avec z_e < l₀.

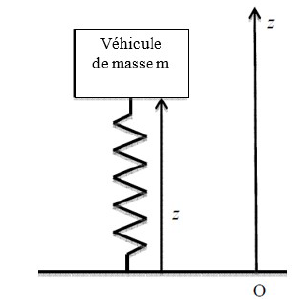
1. Quelles sont les forces auquelles le véhicule est soumis ?
2. Exprimer z_e en fonction de m, g, k et l₀.
Le véhicule est soumis à son poids ( verticale, vers le bas, valeur mg), à la force de rappel exercée par la suspension ( verticale, vers le haut, valeur k(l₀-l)).
A l'équilibre les deux forces se compensent :
mg = k(l₀-l) avec l = z_e.
mg = k(l₀-z_e).
z_e = l₀-mg/k.
3. Lorsque le véhicule est en mouvement, exprimer l'équation différentielle vérifiée par z(t). Exprimer la pulsation w₀ en fonction de k et m.
m d²z/dt² = -mg + k(l₀-z)=k(z_e-z)
d²z/dt² +k/m z =k/m z_e.
w₀ = (k/m)^½.
d²z/dt² +w₀² z = w₀² z_e.
4. Donner la forme de la solution de cette équation sans chercher à déterminer les constantes d'intégration..
Solution générale : z(t) =A cos (w₀t)+ B sinw₀t)+ z_e. avec A et B des constantes réelles.

5. Un opérateur soulève un peu le véhicule jusqu'à la cote z₀ > z_e et le relâche sans vitesse initiale. Déterminer z(t).
z(t) =A cos (w₀t)+ B sinw₀t)+ z_e.
z(t=0)= z₀ ; A + z_e= z₀.
Vitesse dz/dt =-Aw₀sin (w₀t) +Bw₀cos (w₀t)
A t =0 , dz/dt=0 : Bw₀= 0; B=0.
z(t) =(z₀-z_e) cos (w₀t)+ z_e.
On suppose maintenant que la suspension comporte un dispositif qui exerce sur le véhicule une force d'amortisement f =h z' verticale.
6. Quelle est l'unité de h, coefficient de frottement ?
h : force ( N ou kg L s^-2) / vitesse (L/s) ; h s'exprime en kg s^-1.
7. Déterminer la nouvelle équation différentielle vérifiée par z(t) lorsque le véhicule est en mouvement. Faire apparaître la pulsation propre et le facteur de qualité Q.
Le véhicule est soumis à son poids P, à la force de rappel du ressort T et à la force de frottement fluide f.
Lorsque le véhicule est à l'équilibre, la vitesse est nulle, donc f =0. La position d'équilibre est inchangée.

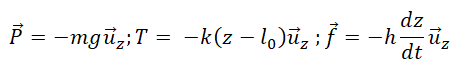
md²z/dt² =-mg-k(z-l₀)-hdz/dt ;
d²z/dt² +h/m dz/dt +k/m z=-g+kl₀/m.
d²z/dt² +h/m dz/dt +k/m z=-g+kl₀/m = k / m z_e.
d²z/dt² +h/m dz/dt +w₀² z=-g+kl₀/m =w₀² z_e.
Q = m w₀ / h.
d²z/dt² +w₀/Q dz/dt +w₀² z=w₀² z_e.
8. Quelles sont les différentes formes de solutions ?
Equation caractéristique : r²+w₀/Q r +w₀² =0.
Discriminant de cette équation : D = (h/m)²-4k/m.
Si D >0, soit h > 2(km)^½ les solutions sont réelles et le régime est apériodique.
Si D <0, soit h < 2(km)^½ les solutions sont complexes et le régime est pseudopériodique.
Si D =0, soit soit h = 2(km)^½le régime est critique.

9. Embarquer les passagers ( masse totale M) peut-il changer la forme de la solution ?
Si la suspension est en régime critique lorsque le véhicule est à vide h = 2(km)^½.
En charge M > m, soit h < 2(kM)^½ le régime devient pseudopériodique.

Le véhicule se déplace horizontalement à la vitesse constante v₁ sur un sol ondulé. La côte du sol est z_s = z₀ cos (wt). La foce de frottement fluide est donnée par f = h(z'-z'_s).
10. Exprimer la force exercée par le ressort sur la masse en fonction de k, z, z_s, l₀ .
La longueur du ressort est l = z-z_s.

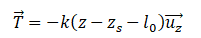
11. Exprimer l'équation différentielle vérifiée par z(t).
Projection de la seconde loi de Newton selon l'axe vertical ascendant :
md²z/dt²=-k(z-z_s-l_o)-mg-h(dz/dt-dz_s/dt)
md²z/dt²+hdz/dt+kz=hdz_s/dt+kz_s+kl₀-mg= hdz_s/dt+kz_s+kz_e.
12. On pose z' = z-z_e. Etablir l'équation diférentielle vérifiée par z' sous la forme md²z'/dt² +h dz'/dt+kz' = Y(t).
dz/dt =dz'/dt ; d²z/dt²=d²z'/dt²car z_e est une constante.
md²z'/dt²+hdz'/dt+kz'=hdz_s/dt+kz_s.
On identifie Y(t) = hdz_s/dt+kz_s
13. Exprimer H = Z' / Z_s.
On pose Z' =Z'_m exp(jwt ) avec Z'_m =Z'_mexp(jf) et Z_s=Z_sm exp(jwt).
L'équation différentielle s'écrit :
md²Z'/dt²+hdZ'/dt+kZ'=hdZ_s/dt+kZ_s.
-mw²Z'+jwhZ'+kZ'=jwhZ_s+kZ_s.
Z' / Z_s=(k+jwh) / (k-mw²+jwh).
On pose l = h /(2m) et w₀²=k/m.
Z' / Z_s=(w₀²+2jwl) / (w₀²-w²+jwl).
Module de cette expression :

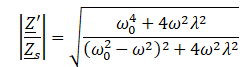
14. Quelles sont les limites de |H| en haute et basse pulsations ?
Si w tend vers zéro : H tend vers 1.
La masse suit le relief du sol ; le ressort possède sa longueur d'équilibre.
Si w tend vers +oo : H tend vers zéro.