Moteur Stirling. Concours ITPE 2024.

Une enceinte étanche est séparée en deux chambres, une chambre chaude ( chauffée par l'extérieur), de volume maximal V₁ et une chambre froide équipée d'un dissipateur thermique de volume maximal V₂. Chaque chambre est munie d'un piston permettant de faire varier son volume et le fluide peut circuler librement d'une chambre à l'autre. Le piston de la chambre froide est le piston de travail, il entraîne le piston de la chambre chaude appelé "déplaceur" car son rôle est de faire circuler le fluide entre les deux chambres. Lors du transvasement le fluide passe de la chambre chaude à la température T₃ à la chambre froide à la température T₁ < T₃ et réciproquement.
Le mouvement du gaz est décrit en 4 phases :
n moles de gaz parfait de coefficient adiabatique g subissent les transformations suivantes :
- compression 1-->2 isotherme réversible à la température T₁.
Echauffement 2-->3 isochore jusqu'à l'état 3 à la température T₃.
Détente 3 --> 4 isotherme réversible à la température T₃.
Refroidissement 4 --> 1 isochore.

1. Représenter l'allure du diagramme du cycle. Justifier que ce cycle est moteur.

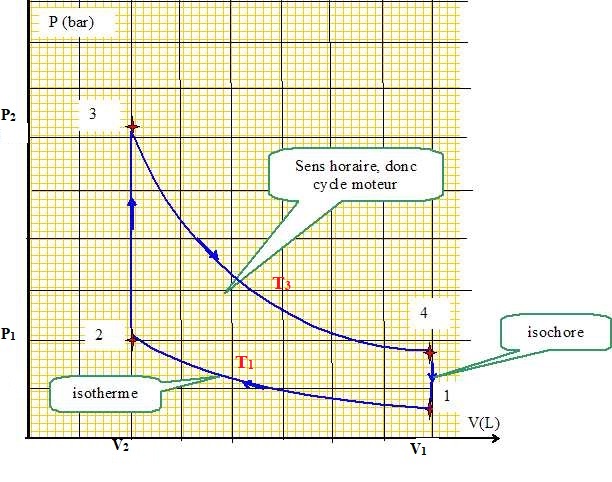On note r= V₁/ V₂.
2. Montrer que la capacité thermique à volume constant s'écrit : Cv = nR / (g-1).
Cp-Cv = nR ; g = C_p/C_v.
g Cv -Cv = nR ; Cv = nR / (g-1).
3. Exprimer W₁₂ et W₃₄ en fonction notamment de r.
Les travaux sont nul au cours des transformations isochores. W₂₃ = W₄₁ =0.
Au cours d'une transformation isotherme :

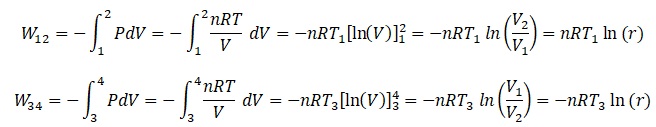4. En déduire les transferts thermiques Q₁₂et Q₃₄. Préciser les signes des différents thermes.
Pas de variation d'énergie interne du gaz parfait au cours d'une isotherme :
Le premier principe de la thermodynamique conduit à :
Q₁₂= -W₁₂ =-nRT₁ln(r) < 0 ;
Q₃₄= -W₃₄ =nRT₃ln(r) > 0 , chaleur reçue par le gaz.
5. Exprimer Q₂₃ et Q₄₁en fonction de g, T₁ et T₃. Préciser leurs signes.
Transformations isochores : W₂₃=W₄₁=0.
Variation d'énergie interne du gaz :
W₂₃ = 0 ; Q₂₃ = DU₂₃ = C_v(T₃-T₁) = nR / (g-1)(T₃-T₁)>0.
W₄₁ = 0 ; Q₄₁ = DU₄₁ = C_v(T₁-T₃)=nR / (g-1)(T₁-T₃) < 0.
6. Définir et exprimer le rendement du moteur en fonction de T₁, T₃, r et g.
Rendement =énergie utile / énergie dépensée = |-W | / (Q₂₃+Q₃₄)
|-W|=nR(T₃-T₁) ln(r) ; Q₂₃+Q₃₄=nR(C_v(T₃-T₁)+T₃ ln(r) ).
Rendement = (T₃-T₁) ln(r) / (C_v(T₃-T₁)+T₃ ln(r)).

7. Définir le rendement de Carnot. L'exprimer en fonction de T₁ et T₃. Commenter.
Le cycle de Carnot est un cas idéal dans lequel toutes les transformations sont réversibles. Il indique quel est le rendement maximal possible. Les transformations réelles ne sont pas réversibles.
Rendement maximal= 1-T₁/T₃.
Un moteur de Stirling peut contenir un régénérateur. La chaleur perdue par le gaz lors du refroidissement isochore est récupérée par le gaz lors du chauffage isochore. Si le régénérateur est idéal, cette récupération est totale.
8. Que devient le rendement du cycle dans ce cas ?
Le rendement sera égal au rendement du cycle de Carnot.
Dans la réalité, l'hypothèse faite " récupérer totalement la quantité d'énergie échangée par chaleur lors du refroidissement isochore pour la restituer au cours du chauffage isochore", est en réalité impossible à réaliser sur le plan pratique. Il faudrait pour cela que le régénérateur ait une efficacité de 100 %.