Mathématiques.
Concours ingénieur territorial
2025.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| ... |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. Partie A. 7 points.
Soit g(x) la fonction définie sur ]0 ; +oo[ par g(x) = x2-1+3 ln(x)
1. Calculer g(1) et les limites de g en 0 et +oo.
g(1) = 1-1+3ln(1)=0.
Limite en zéro :
x2 =0 ; ln(x) tend vers -oo ; g(x) tend vers -oo.
Limite en +oo : x2-1 tend vers +oo ; ln(x) tend vers +oo ; g(x) tend vers +oo.
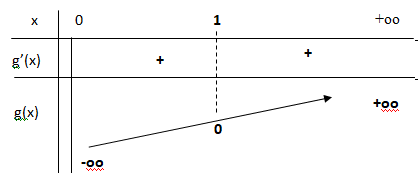
2. Calculer g'(x) et établir le tableau de variation de g.
3. En déduire le signe de g(x) sur ]0 ; +oo[.
g'(x) = 2x+3/x=(2x2+3) /x.
g'(x) est strictement positive et g(x) est strictement croissante.
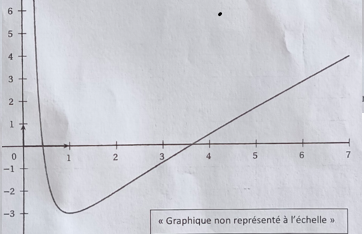
On considère la fonction f définie sur ]0 ; +oo[ par f(x) = x-2 -(2+3ln(x)) / x.
On donne la représentation graphique de f.
Unités : 2 cm en abscisses et 1 cm en ordonnées.
4. Montrer que pour tout réel x >0, f '(x) = g(x) x2.
On pose u = 2+3ln(x) et v = x ; u' = 3 / x ; v'=1.
(u'v-v'u) / v2=( 3-2-3ln(x)) /x2 =( 1-3ln(x) ) / x2.
f '(x) = 1-(1-3ln(x) ) / x2=[x2- 1+3ln(x) ] / x2=g(x) / x2.
En déduire le tableau de variation de la fonction f sur ]0 ; +oo[.
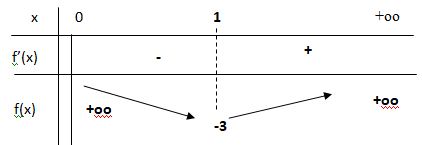
5. f(x) = 0 admet deux solutions a et ß.
Justifier par le calcul l'encadrement 0,412 < a < 0,413.
f(0,411)=0,035 ; f(0,412) =0,0144 ; f(0,413)=-0,0060.
Partie B. 3 points.
a = 0,41 ; ß = 3,62.
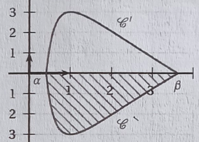
Le chef de cuisine souhaite réaliser des palets en forme de goutte d'eau.
Pour obtenir cette forme, on considère la courbe représentative de la fonction f sur l'intervalle [ a ; ß] ainsi que son symétrique par rapport à l'axe des abscisses.
1. On pose u(x) = 1,5( ln(x))2. Calculer la dérivée u'(x).
On pose v = ln(x); v' = 1/x.
u'(x) =1,5 * 2 v v' =3 ln(x) / x.
En déduire une primitive F de f sur ]0 ; +oo[.
f(x) = x-2 -2/x-3ln(x) / x.
F(x) =0,5x2-2x-2ln(x)-1,5 ln(x2).
2. Calculer l'aire de la partie supérieure d'un palet.
F(ß) -F(a) =F(3,62)-F(0,41)= -7,12-3,72= - 10,84 unités d'aire.
Aire d'un palet : 2 x10,84 = 21,68 unités d'aire = 21,68 x2 =43,36 cm2.
3. Chaque palet a une épaisseur de 5 mm. Calculer le volume d'un palet.
43,36 *0,5=21,68 cm3.
4. Le chef doit fabriquer 80 palets avec 1 litre de pâte. Est-ce possible ?
1000 / 21,68 ~46 palets.
|
...
|
....
|
Exercice 2. 3 points.
On note M2(R) l'ensemble des matrices d'ordre 2 à coefficients réels.
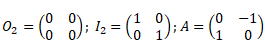
On note C la partie de M2(R) définie par : C ={M appartient à M2(R) , AM=MA}
Partie A. 2 points.
1. Calculer A2.
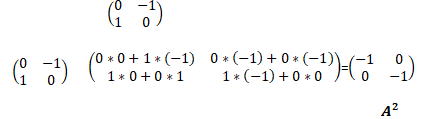
2. En déduire que A est inversible et calculer son inverse.
Déterminant de A : 0*0 -1*(-1) = 1
Le déterminant n'étant pas nul, la matrice A est inversible.
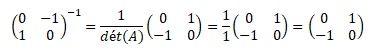
3. La matrice A est-elle diagonalisable ?
Recherche des valeurs propres de A :
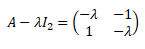
Les valeurs propres sont solutions de l'équation (-l)2-1=0 soit l = 1 et l = -1.
A est une matrice de type (2,2) et possède deux valeurs propres distinctes : elle est donc diagonalisable.
4. Démontrer que C est un sous-espace vectoriel de M2(R).
C(A) est inclus dans M2(R).
De plus A xO2 = O2 = O2xA donc O2 appartient à C(A).
Soient M1 et M2 deux éléments de C(A) et l un réel. Alors :
(lM1+M2)A =lM1A +M2A =lAM1 +AM2 =A(lM1+M2).
Donc lM1+M2 appartient à C(A).
On en conclut que C(A) est un sous espace vectoriel de M2(R).
Partie B. 1 point.
1. Résoudre l'équation AM = MA d'inconnue M.
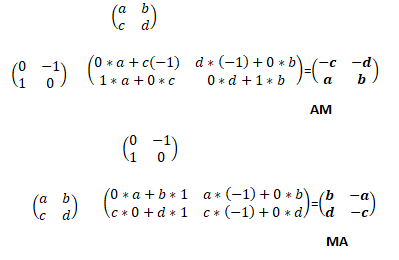
On identifie : b = -c ; a=d.
2. Monter que (I2, A) est une base de C.
3. En déduire la dimension du sous-espace vectoriel C.
|
|
|
|