Mathématiques. annale zéro, DNB 2026.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

Exercice 1. 6 points.
Question 1.
  quel est le tiers de 18 ?
18 / 3 = 6.

Question 2.
Un film dure 240 min. Quelle est sa durée en heures ?
240 / 60 = 4 heures.

  Question 3.
  Les notes obtenues par un élève sont : 8; 12; 6; 19; 15.
 Que vaut la médiane de cette série de notes ?
Ordonner : 6 ; 8 ; 12 ; 15 ; 19.
La médiane est 12.

Question 4.

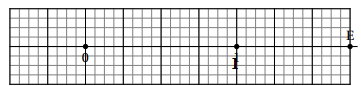
Sur cette droite graduée, l’abscisse du point E est : 7 / 4.

Question 5.
Dans le triangle ABC, rectangle en B, calculer l'angle BCA.

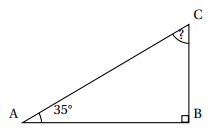
180 -90 -35 =90-35=55°.

Question 6.
Dans le triangle ABC, rectangle en A, quel calcul doit-on effectuer pour déterminer le cosinus de l’angle ABC ?

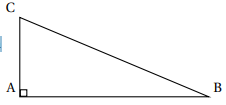
cos (ABC) =côté adjacent / hypothénuse = AB / BC.

Question 7 Sur la figure ci-dessous, dans le triangle ADE les droites (DE) et (CB) sont parallèles. Déterminer la longueur AD.

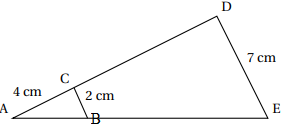
Propriété de Thalès : AD / AC = DE / BC ; AD = DE * AC / BC = 7 * 4 / 2=14 cm.

Question 8.
 Dans un collège, 25 % des 300 élèves participent à une olympiade de mathématiques. Combien d’élèves ne participent pas a cette olympiade ?
300 x(1-0,25) = 300 x0,75=225.

Question 9
Une élève souhaite réaliser un programme avec un logiciel de programmation pour dessiner un carré. Par quelles valeurs doit-on compléter les lignes 3 et 5 pour obtenir un carré ?


Exercice 1 : 3 points.
   Dans le cadre d’un projet de labellisation « Éducation au développement durable », un collège réalise deux enquêtes sur une période donnée.
1. La première enquête porte sur le gaspillage alimentaire à la cantine. Pendant sept semaines, on relève la masse totale, en kilogramme, d’aliments jetés chaque semaine :
Semaine
 1
 2
 3
 4
 5
 6
 7
Masse (kg)
 62
 59
 74
 68
 55
 61
 71
 Ce collège s’est donné comme objectif que la moyenne, par semaine, de déchets alimentaires sur les 7 semaines ne dépasse pas 65 kg. Montrer que ce collège a atteint son objectif.
Moyenne= (62+59+74+68+55+61+71) / 7~64 kg < 65 kg.
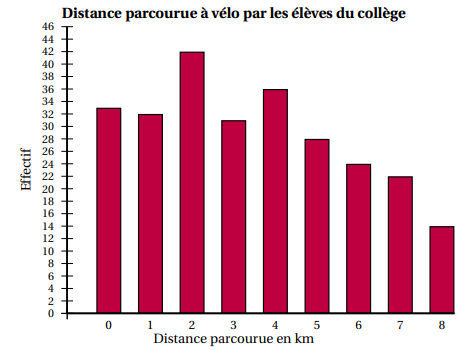
2. La seconde enquête porte sur les déplacements des élèves à vélo entre le domicile et le collège. Le diagramme ci-dessous représente, pour chaque distance, l’effectif des élèves qui parcourent cette distance en vélo pour aller au collège. (Les élèves qui n’utilisent pas le vélo pour se rendre au collège parcourent 0 km à vélo.)

a. Déterminer l’effectif total d’élèves de ce collège.
33+32+42+31+36+28+24+22+14=262.
b. Pour ce collège, l’affirmation « Plus de 30 % des élèves ont parcouru au moins 5 km à vélo pour se rendre au collège » est-elle vraie ? Justifier la réponse en précisant la démarche.
28+24+22+14=88 élèves ont parcouru au moins 5 km.
88 / 262 ~0,34 ( 34 %). Affirmation vraie.

Exercice 2 : 3 points.
 On donne un programme de calcul :
choisir un nombre ; le multiplier par 2 ; élever le résultat au carré ; retrancher 9 ;  afficher le résultat
1. Lorsque le nombre choisi est 4, vérifier le programme affiche 55, en précisant chacune des étapes de calcul.
4x2=8 ; 82=64 ; 64-9=55.
2. On appelle x le nombre choisi au départ.
a. Écrire, en fonction de x, le résultat obtenu par le programme.
2x ; (2x)2 = 4x2 ;4x2-9=(2x+3)(2x-3)..
b. Parmi les quatre expressions suivantes, laquelle correspond au résultat obtenu par le programme ?
 A = 55 ; B = (2x +3)2 ; C = (2x −3)(2x +3) ; D = (2x—3)2.

Exercice 3. 3 points.
 On considère les fonctions f et g suivantes :f(x)= 4x +3 g : g(x)= 6x.
 Leurs représentations graphiques (d1) et (d2) sont tracées ci-dessous :

1. Parmi ces deux fonctions, laquelle représente une situation de proportionnalité ?
Fonction linéaire g(x) = 6 x.
 2. Calculer l’image de 0 par la fonction g.
g(0) = 0.
 3. Déterminer l’antécédent de 0 par la fonction f .
0 = 4x+3 ; 4x=-3 ; x = -3 /4.
4. Associer à chaque droite la fonction qu’elle représente. Justifier la réponse.
(d1), droite passant par l'origine ; fonction linéaire g(x).
 (d2), droite ne passant pas par l'origine ; fonction affine f(x).
5. Déterminer graphiquement les coordonnées du point d’intersection des droites (d1) et (d2).
(1,5 ; 9).

Exercice 4 : 3 points
 ABCD est un carré de côté 9 cm;
 
1. a. Le polygone IJKLMNOP est-il régulier, c’est-à-dire a-t-il tous ses côtés de même longueur ? Justifier la réponse.
 IJ = 3 cm ;
JK, diagonale d'un carré de côté KB =3 cm ; JK = 3 x 2½ ~4,2 cm.
JK diffère de IJ : le polygone IJKLMNOP n'est pas régulier.
 b. Justifier que l’aire de la surface IJKLMNOP grisée sur la figure ci-contre est égale à 63 cm2 .
Aire du carré ABCD =9 x9 = 81 cm2.
Aire du triangle AIP = AI x IP /3 = 3 x3 /2 = 4,5 cm2.
Aire hachurée = 81-4 x4,5 =63 cm2 .

 2. Les diagonales du carré ABCD se coupent en S. On a tracé le cercle de centre S et de diamètre 9 cm.
a. Déterminer l’aire du disque de centre S et de diamètre 9 cm.
p D2 /4 =3,14 x 92/4=63,6 cm2.
b. Montrer que la différence entre l’aire du polygone IJKLMNOP et l’aire du disque représente moins de 1 % de l’aire du disque.
Aire du disque - aire du polygone IJKLMNOP =63,6-63=0,6 cm2.
0,6 / 63,6 x100=0,94 % < 1 %.


  
menu