Optique : bi-lentilles de Billet : interférences. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

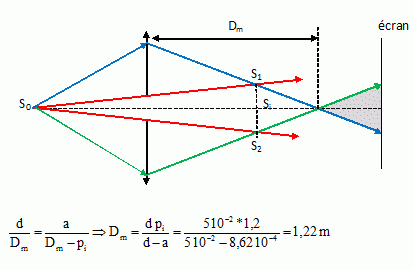
Une lentille mince convergente est coupée en deux moitiés identiques. Le diamètre d'ouverture est égal  à d = 5 cm. Les deux demi-lentilles sont écartées symétriquement, perpendiculairement  à l'axe x'Ox de la lentille. Une fente fine S0 est située sur l'axe x'Ox, à 60 cm devant les deux demi-lentilles ; S0 est éclairée par une lumière monochromatique ( l = 546 nm) ; la distance focale de cett lentille est fi = 40 cm. On observe des franges d'interférences sur un écran E, perpendiculaire à l'axe x'Ox, situé à la distance D =1,50 m des demi-lentilles. l'interfrange mesuré sur E vaut i = 0,19 mm. Calculer l'écartement b des demi-lentilles. Cet écartement demeurera constant dans la suite du problème. S1S2 = a. S1 et S2 images de S0, données par chaque lentille.  Ecrire la formule de conjugaison des lentilles minces : 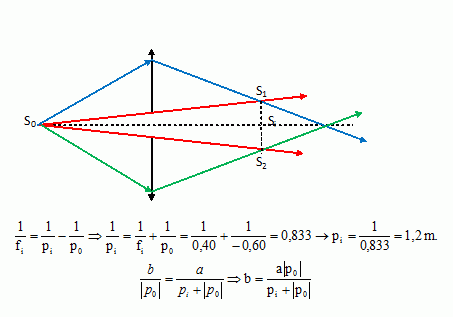De plus i = l D/a avec D = 1,5-1,2 = 0,30 cm, distance de Si à l'écran ; d'où a = l D/i = 546 10-9*0,3 / 0,19 10-3 =8,62 10-4 m. par suite : b = 8,62 10-4 * 0,6 /(0,6 +1,2) =2,8737 10-4 ~2,9 10-4 m. Calculer la distance minimale Dm entre l'écran et les demi-lentilles pour que l'on puisse observer des franges sur l'écran.   On déplace l'écran parallèlement à lui même. Comment varie la largeur l du champ d'interférences en fonction de la distance D ? 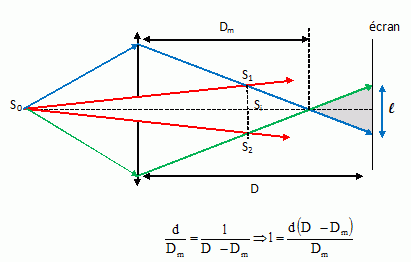Calculer le nombre de franges brillantes que l'on doit théoriquement observer lorsque D = 1,5 m. Largeur de champ l = 0,05 *(1,50-1,22) / 1,22 =1,147 10-2 ~ 1,15 10-2 m = 1,15 cm. interfrange i = 1,9 10-4 m. La frange centrale est brillante ; 1ère frange brillante à 1,9 10-4 m ; 2ème frange brillante à 3,8 10-4 m ; 3ème frange brillante à 5,7 10-4 m ; 4ème frange brillante à 7,6 10-4 m ; 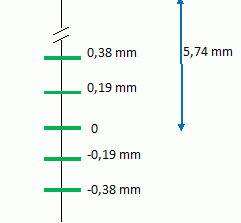5,74 / 0,19 = 30 donc 30 + 30 + 1 = 61 franges. On éclaire la fente en lumière blanche. On suppose que l'indice du verre est constant. Expliquer les phénomènes observés sur l'écran. Les systèmes de franges d'interférence associés aux différentes longueurs d'onde comprises entre 400 nm et 750 nm se superposent. Au centre, différence de marche nulle pour toutes les radiations, les intensités de toutes les radiations sont maximales : la superposition restitue la lumière blanche de la source. Or les interfranges  i = lD/a, varient proportionnellement  aux longueurs d'onde. Les franges sont irrisées de bleu vers le centre et de rouge à l'extérieur. Ensuite les franges sont brouillées : on observe une zone blanche dans laquelle l'analyse à l'aide d'un spectroscope permet de distinguer des raies noires ( cannelures sombres) On place un spectroscope dans le champ d'interférences, parallèlement à l'axe de la frange centrale, en un point d'abscisse x0. Calculer le nombre de cannelures si x0 = 1 mm. différence de marche d = ax0/D =8,62 10-4 *10-3 / 0,30 =2,873 10-6 m Si d = (2n+1) l/2, on observe une frange sombre. l = 2 d / (2n+1)= 5,747 10-6 / (2n+1)  n=0 : l = 5,747 10-6 m = 545 nm.  n=1 : l = 1,91 10-6 /3 = 191 nm.( domaine UV)

retour -menu