|
. .Chute, oscillateur mécanique, poussée d'Archimède, équilibre d'un solide : concours kiné EFOM 2012. |
||||||||
|
||||||||
|
.
Chute libre. Oscillateur
mécanique horizontal. .
Oscillateur mécanique horizontal. Dans un champ de pesanteur uniforme, on fixe à un support un ressort de raideur k et de masse négligée. Sa longueur à vide est L0. A son extrémité libre, on accroche une masse supposée ponctuelle m, pour réaliser un oscillateur mécanique horizontal. La masse peut alors osciller à la vitesse v sur un rail horizontal. Ce dernier exerce sur m une force de frottement du type 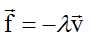 On écarte la mass m d'une distance A à partir de sa position d'équilibre O, prise comme origine du repère d'espace. On la lâche sans vitesse initiale à l'instant t=0. A) L'équation différentielle modèlisant le mouvement de la masse m est : x" -l x' +k/m x = 0. Faux.  B) L'équation différentielle modèlisant le mouvement de la masse m est : x" +l x' +k/m x = 0. Faux. C) L'équation différentielle modèlisant le mouvement de la masse m est : x" -l /m x' +k/m x = 0. Faux. On suppose le mouvement de m harmonique et l'équation horaire de sa position de la forme x = A sin (2pt/T0) où A est l'amplitude des oscillations et T0 la période propre. D) On a T0 = 2 p(m/k)½. Vrai. D) On a T0 = 2 p(k/m)½. Faux Plongeur dans la mer Morte. En peline mer Morte, un plongeur de masse m =100 kg s'immerge le long d'un câble vertical. Son équipement est réduit à une ceinture de plomb dont on négligera le volume. Masse volumique : de l'eau de mer r0 = 1250 kg m-3 ; d'un être humain rh = 1,0 103 kg m-3 ; du plomb rPb = 11350 kg m-3 ; A) On peut affirmer que le volume d'eau déplacé par l'immersion du plongeur est strictement égal au volume du plongeur. Vrai. Le volume du plomb peut être négligé. La masse du plomb mPb que le plongeur doit emmener pour descendre sous l'eau à vitesse constante est : 25,0 kg ; 2,80 kg ; 28,0 kg 14,0 kg. On néglige les frottements. A vitesse constante le poids est opposé à la poussée d'Archimède. On note V le volume du plongeur. Poussée : V g r0. Poids : V g rh + mPb g. V r0 = V rh +mPb ; mPb = V( r0 - rh ) ; V = m / rh = 100 / (1,0 103 )=0,10 m3. mPb =0,10 (1250-1000) =25 kg.
|
||||||||
On lance un mobile auto-porteur sur un plan incliné d'un angle a = 35° par rapport à l'horizontale. Le mobile est lancé suivant un angle inconnu et possède une vitesse initiale de norme v0. On relève par étincelages les positions Mi du centre d'inertie G du mobile. L'intervalle de temps entre chaque position est 50 ms.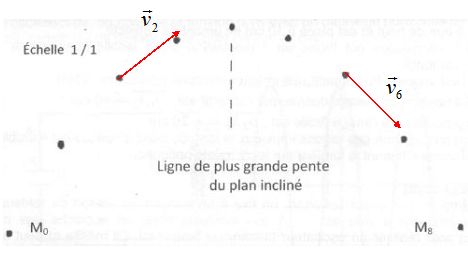 A) La norme v2 de la vitesse en M2 vaut approximativement 0,8 m/s. Faux. v2 = (M1M2+M2M3) / (2*0,050) = (0,03+0,020) / 0,1 = 0,5 m/s. B) La norme v2 de la vitesse en M2 vaut approximativement 0,4 m/s. Vrai. C) Les vecteurs vitesses v2 et v6 sont identiques. Faux. Ils n'ont pas la même direction. D) Le vecteur différence 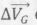 entre deux positions Mi et Mi+1 est un vecteur constant. Vrai. entre deux positions Mi et Mi+1 est un vecteur constant. Vrai.Les forces étant constantes, le vecteur accélération est constant. 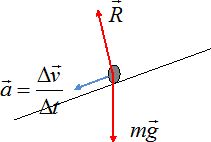 E) Le vecteur différence 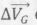 entre deux positions Mi et Mi+1 est colinéaire à la ligne de plus grande pente du plan incliné. Vrai. entre deux positions Mi et Mi+1 est colinéaire à la ligne de plus grande pente du plan incliné. Vrai.On enregistre au fil du temps, la position d'un système oscillant ponctuel libre. 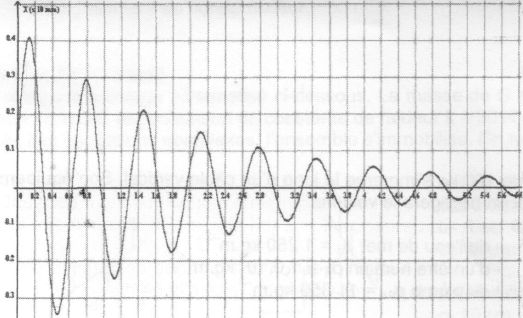 A) On assiste à des oscillations libres amorties. Vrai. B) On asiste à des oscillations libres en régime pseudo-périodiques. Vrai. C) On asiste à des oscillations libres en régime critique. Faux. D) On asiste à des oscillations libres en régime apériodique. Faux. E) On peut dire que la somme des énergies du système est constante. Faux. L'énergie mécanique diminue du fait des frottements. |
||||||||
|
|
||||||||