Etude d'un pendule simple en coordonnées polaires, Concours ITPE 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. . Alors qu'il  19 ans, Galilée découvre que les oscillations des lustres de la cathédrale de Pise sont régulières. De retour chez lui, il décide alors de comparer les oscillations de deux pendules et travaille alors sur la loi de l'isochronisme. Il trouve ainsi la formule sur les lois du pendule simple : T = 2 p (L/g)½ avec L longueur du pendule et g l'intensité de la pesanteur. On considère un pendule simple qui oscille dans un milieu où les forces de frottements sont inexistantes et où la poussée d'Archimède est négligeable. Le pendule est constitué d'un objet ponctuel de masse m, accroché par l'intermédiaire d'un fil à un point fixe O. On suppose le fil rigide sans masse. Sa longueur est L = 1 m. On note q l'angle du fil OM avec la verticale. L'ensemble est situé dans le champ de pesanteur  terrestre, supposé uniforme. On écarte alors le pendule de  sa position d'équilibre d'un angle q0 et on le lche sans vitesse initiale. On utilisera le repère polaire défini sur le schéma ci-dessous. Le référentiel R utilisé sera considéré comme galiléen. Définir ce qu'est un référentiel galiléen. Dans un référentiel galiléen, les lois de Newton s'appliquent. Faire un bilan des forces appliquées à l'objet de masse m et les représenter sur un schéma. l'objet de masse m est soumis à son poids et à la tension du fil. Montrer que le poids de l'objet s'écrit : La projection du poids sur l'axe OM est : mg cos q ; la projection du poids sur l'axe de vecteur unitaire uq est -mg sin q. Elément de cinématique en coordonnées polaires. Donner l'expression du vecteur position OM. Donner l'expression du vecteur vitesse pour un mouvement circulaire. Le vecteur vitesse est à chaque instant tangent au cercle. Il a toujours le sens du mouvement. Durant l'intervalle de temps très petit dt, M décrit l'arc de cercle L dq.   La valeur de la vitesse est alors v = Ldq/dt = L q'. Par suite : Montrer que l'expression du vecteur accélération en coordonnées polaires pour un mouvement circulaire s'écrit : Le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps. Exprimer le vecteur accélération dans la base de Frenet. . Utilisation du principe fondamental de la dynamique. Enoncer le principe fondamental de le dynamique. Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées au système est égale au produit de la masse du système par l'accélération de son centre d'inertie. Montrer que l'équation du mouvement vérifiée par l'angle q(t) en fonction du temps peut s'écrire : q" +g/L sin q =0. Utilisation du moment cinétique. 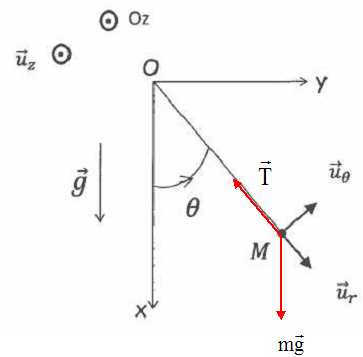Enoncer le théorème du moment cinétique appliqué au point M dans le référentiel R. La dérivée par rapport au temps du moment cinétique du point matériel M par rapport au point fixe O est égal au moment, par rapport à ce point, de la somme vectorielle des forces agissant sur le point matériel M . 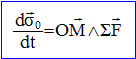. Montrer que la trajectoire du point matériel est plane. Retrouver l'équation du mouvement vérifiée par l'angle q(t) en fonction du temps. (1) : j'exprime le moment cinétique. (2) Le moment, par rapport à O, de la tension est nul : cette force rencontre le point O. (3) : j'exprime le moment en O du poids. (4) : j'applique le théorème du moment cinétique (4) montre que la trajectoire du point M est plane, celui de la figure. (4) donne l'équation différentielle vérifiée par l'angle q(t) en fonction du temps : q " + g/l sin q = 0 Etude énergétique. Exprimer l'énergie cinétique du point matériel M en fonction de m, q' et L. Ec = ½mv2 avec v = Lq' ; Ec = ½mL2q'2 . Exprimer l'énergie potentielle de pesanteur en fonction de m, g, L et q. On prend l'origine de l'énergie potentielle pour q = 0, c'est à dire M en M0. 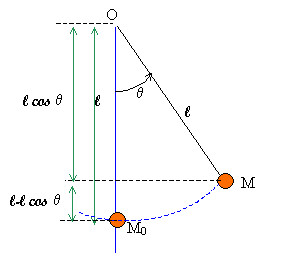Ep = mgl(1-cosq). En déduire l'expression de l'énergie mécanique du point matériel M. Em= ½m(Lq ')2 + mgL(1-cosq). Retrouver l'équation du mouvement vérifiée par l'angle q(t) en fonction du temps. L'énergie mécanique se conserve ; dériver  son expression par rapport au temps. 0 = ½mL22 q' q" +mgLsin q q' ; simplifier par mL q' : L q" +g sin q = 0. Oscillations de faibles amplitudes. Déterminer l'expression de la nouvelle équation différentielle vérifiée par q(t). sin q ~q radian pour les petits angles. Par suite : L q" +g  q = 0 ou q" +g/ L q = 0. Donner l'expression de la pulsation w et de la période T0. w = (g/ L)½ ; T0 = 2 p / w = 2 p(L/g)½. Quelle doit être la longueur L pour que le pendule batte la seconde ? Le pendule doit effectuer un aller simple en 1,00 s, sa période T0 doit être égale à 2,00 s. On prendra g = 9,81 m s-2 ( valeur à Paris ). L = g(T0/(2p))2 =9,81 (1/3,14)2 =0,994 m.

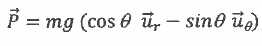
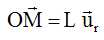
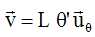
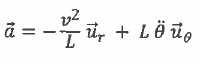
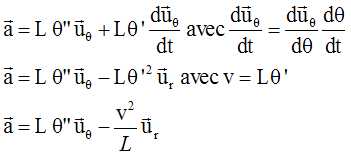
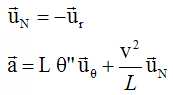
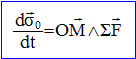menu