Vidange d'un
réservoir, densimètre.
Concours national Deug
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Un réservoir de
section S1 est percé à la base d'un petit trou de section S2.
On note h0 la hauteur initiale du liquide dans le réservoir.
On note vA la vitesse au point A à la surface libre et vB
la vitesse du liquide au point B. Soit h la hauteur du liquide à
l'instant t. On suppose l'écoulement incompressible et stationnaire. On
néglige la variation de la pression atmosphérique avec la hauteur.
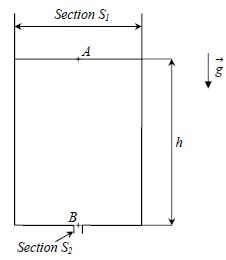
Ecrire la variation
du débit volumique entre A et B.
Le débit volumique est constant : Q = S1vA = S2
vB soit vB
=vA
S1
/S2.
Appliquer le
théorème de Bernoulli entre A et B. On note µ la masse volumique
du fluide.
½µv2A +µgh +pA =½µv2B
+µgzB +pB ; or zB = 0 et pA
= pB = pression atmosphérique.
½µv2A
+µg h =½µv2B
= ½µ(vA
S1
/S2)2.
v2A
((S1
/S2)2-1)=2g h. On
pose ß2=(S1
/S2)2-1
; ß2v2A
=2gh.
En déduire une
équation différentielle du premier ordre en h.
vA
=-dh/dt ; ß2(dh/dt)2
=2gh ; (dh/dt)2
-2gh/ß2 =0.
On pose K = - 2g/ß2
=2g /(1-(S1
/S2)2).
dh/dt
= (2gh)½/ß ou encore (dh/dt)2 +Kh=0.
Résoudre cette
équation et déterminer la loi d'évolution de h.
dh / h½ = (2g)½ / ßdt ; intégrer entre h et h0
:
2 [h½]hh0 = 2h0½
- 2h½
=(2g)½
/ ß t.
h½
=h0½
-(g/2)½
/ ß t = h0½
+½K½ t.
En
déduire le temps T de vidange du réservoir.
0 =h0½+½ K½ T ; T = -2(h0 /
K)½ =2(h0((S1
/S2)2-1)
/(2g))½.
|
| .
. |
|
|
La densité d'un liquide est le rapport de sa masse volumique r sur celle r0 de l'eau.
Un densimètre est constitué d'une tige cylindrique de section s, de hauteur hM et d'une boule lestée. L'ensemble a pour volume v et pour densité d0.
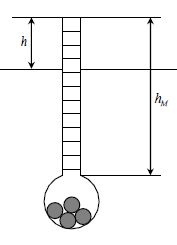
Lorsque
le densimètre est plongé dans un liquide de densité d, le système étant
au repos, une certaine hauteur h de la tige émerge du liquide. On lit
directement la densité sur les graduations inscrites sur la tige
cylindrique.
Déterminer la masse m du densimètre en fonction de d0, r0 et v.
m = v r = v d0 r0.
Exprimer la poussée d'Archimède lorsque le densimètre est plongé dans le liquide en fonction de r0, v, h, s, d et g.
La poussée est égale au poids du volume de fluide déplacé. F = d r0 vfluide g.
vfluide =v-h s ; F = d r0 (v-h s) g.
Elle est verticale et orientée vers le haut.
En déduire l'expression de d en fonction de h, H =v/s et d0.
A l'équilibre la poussée d'Archimède compense le poids du densimètre.
d r0 (v-h s) g =v d0r0.
d(v/s-h = v/s d0 ; d (H-h) =Hd0 ; d = Hd0 /(H-h).
Dans quel intervalle doit se trouver d pour être mesurable.
h doit être compris entre zéro et hM ;
h = 0 conduit à d=d0 ; h = hM conduit à : d = Hd0 /(H-hM).
|
.
|