Mathématiques, Concours audioprothésiste Bordeaux 2014.

Mathématiques
Concours audioprothésiste Bordeaux 2014.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.
.

Calculs.
1. 0,5 ln(16) -ln(2) +2 ln (2^½) est :
A. nul ; B. strictement négatif ; C. égal à 4 ln(2) ; D. égal à 2 ln(2) ; vrai
E. aucune des propositions précédentes.
ln (16^0,5)-ln(2) +ln((2^0,5)²) = ln(4) = ln(2²) = 2 ln2.

2. Ln(25)-1,5 ln(5) -ln(5^½) est :
A. nul, vrai ; B. strictement positif ; C. strictement négatif ; D. égal à 2 ln(5) ;
E. aucune des propositions précédentes.
ln(5²) -ln(5^1,5) -ln(5^½) =ln(5²) -ln(5^1,5x 5^½)=ln(5²) -ln(5²)=0.

3.

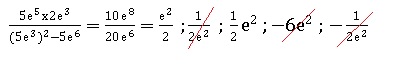
4. [ln(0,5)]² -2ln(0,5) est :
A. nul ; B. strictement positif, vrai ; C. strictement négatif ;
D. n'existe pas;
E. aucune des propositions précédentes.
On pose X = ln(0,5) ; X²-2X = X(X-2).
Or X = -0,693 : X(X-2) >0.

5.
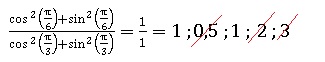
Equations, inéquations, logique.
6. L'ensemble des solutions de l'inéquation 1 / x <2 est
A.]0 ; 0,5 ] ; B. [0 ; 0,5] ; C. [0,5 ; +oo[ ; D. ]-oo ; 0,5[ ;
E. aucune des propositions précédentes. Vrai.
Pour x positif : 2x > 1 ; x > 0,5.
Pour x négatif : 1 >2x ; x < 0.

7. L'ensemble des solutions de l'inéquation exp(x²)< 1 est :
A. infini ; B. 0 vrai ; C. 1 ; D. 2 ;
E. aucune des propositions précédentes.
x² < ln (1) ; x² < 0 ; x =0.

8. L'équation 3z² +2z +2 =0 admet :
A. deux solutions distinctes dans C. Vrai ; B. deux solutions distinctes dans R ;
C. une unique solution dans C ; D. une unique solution dans R ;
E. aucune des propositions précédentes.
D = 2²-4 x2 x3 =-20 = 20 i².
z₁ = -1+i 5^½ ; z₁ = -1-i 5^½ .

9. P₁ et P₂ sont deux propositions et a et b deux réels. De manière générale :
On pose P₁: " a² = b²" et P₂ "a=b".
A. seule P₁ implique P₂ ; B. seule P₂ implique P₁ vrai ; C. P₁ et P₂ sont équivalentes ;
D. P₁ et P₂ sont toujours fausses ;
E. aucune des propositions précédentes.
a² = b² conduit à a= ±b.

.
.

Suites.
On considère les suites suivantes, pour n >1 :
u_n = 1-2 / n ; v_n = 3+3 /(n+1) ; u_n < w_n < v_n.
10. On a alors :
A. u et v sont croissantes ; B. u et v sont décroissantes.
C. u est croissante et v est décroissante. Vrai.
D. u est décroissante et v est croissante.
E. aucune des propositions précédentes.
u₁ = -1 ; u₂ =0 ; u₃ =1/3.... u_n tend vers 1.
v₁ = 4,5 ; v₂ =4 ; v₃ =3,75....v_n tend vers 3.

11. La suite w est nécessairement :
A. convergente. Vrai.
B. divergente vers +oo.
C. divergente vers -oo.
D. divergente sans limite
E. aucune des propositions précédentes.
La suite w est bornée par 1 et 3.

Complexes et géométrie.
12. L'écriture exponentielle de 2-2i est :

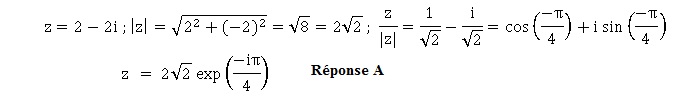
Dans les 4 items suivants on considère les nombres complexes z₁ = 2 exp(ip/9) et z₂ = -2 exp(-ip/9)
13. z₁²⁷ est
A. un réel strictement positif ;
B. un réel strictement négatif ; vrai ;
C. un imaginaire pur ;
D. nul ;
E. aucune des propositions précédentes.
2²⁷ exp((ip/9 x27) = 2²⁷ exp((3ip) =2²⁷ exp((ip) = -2²⁷ .

14. z₁¹⁸ est
A. un réel strictement positif ; vrai ;
B. un réel strictement négatif ;
C. un imaginaire pur de partie imaginaire strictement positive;
D. un imaginaire pur de partie imaginaire strictement négative;
E. aucune des propositions précédentes.
2¹⁸ exp((ip/9 x18) = 2¹⁸ exp((2ip) = 2^18. .

15. On a :
A. z₁ = z₂; B. z₁ = - z₂;
C. z₁ = conjugué de z₂;
D. z₁ = -conjugué de z₂;
E. aucune des propositions précédentes. Vrai.
z₁ = 2( cos ( p/9) +i sin (p/9) ; z₂ = -2( cos ( -p/9) +i sin (-p/9) = 2( -cos ( p/9) +i sin (p/9).

15. On a :
A. z₁ = z₂; B. z₁ = - z₂;
C. z₁ = conjugué de z₂;
D. z₁ = -conjugué de z₂;
E. aucune des propositions précédentes. Vrai.

16. z₁ +z₂ est un :
A. reél strictement positi f; B. un réel strictement négatif ;
C. un imaginaire pur de partie imaginaire strictement positive ; vrai
D. un imaginaire pur de partie imaginaire strictement négative ;
E. aucune des propositions précédentes. Vrai.
2( cos ( p/9) +i sin (p/9)+2( -cos ( p/9) +i sin (p/9) =4isin (p/9)~2,47 i.

17. L'écriture algébrique du nombre complexe z est :

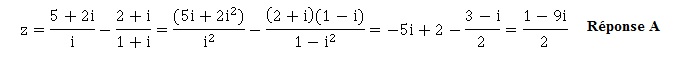
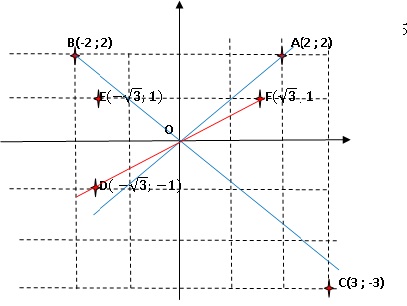
On se place dans le plan complexe d'origine O.
Affixe de A : z_A = 2+2i ; affixe de B : z_B =-2+2i , affixe de C : z_C = a-3i avec a un réel ;
affixe de D : z_D = -3^½-i ; affixe de E : z_E = -3^½+i ; affixe de F : z_F = 3^½+i.
18. Le triangle AOC est rectangle en O si a est égal à : :
A. 2 ; B. 3 vrai ; C. -2 ; D. -3; E. aucune des propositions précédentes.
OA² =2²+2² = 8 ; OC² =a²+(-3)² = 9+a² ; AC² = (a-2)² +(-3-2)²=a²-4a+29.
OA² +OC² =AC² ; 17+a² =a²-4a+29 ; 4a=12 ; a=3.

On prend pour la suite la valeur de a telle que le triangle OAC est rectangle en O.

19. On a :
A. Le triangle AOB est rectangle en A ; B. Le triangle AOB est rectangle en O vrai ; C. Le triangle DOE est rectangle en D ;
D. Le triangle AOB est équilatéral ; E. aucune des propositions précédentes.

20. On a :
A. Le triangle AOF est rectangle ; B. Le triangle DOE est rectangle en O ; C. Le triangle AOF est isocèle ;
D. Le triangle DOE est équilatéral ; E. aucune des propositions précédentes. Vrai.

21. On a :
A. Le triangle AOC est équilatéral ; B. Le triangle DOB est rectangle ; C. Le triangle AOB est isocèle vrai ;
D. Le triangle AOB est équilatéral ; E. aucune des propositions précédentes.
OA² =2²+2² = 8 ; OB² =(-2)²+2² = 8 ; AB² = (-4)² +(0)²=16.

22. On a :
A. Les points A, O et D sont alignés ; B. Les points B, O et C sont alignés ; C. Les points E, O et B sont alignés ;
D. Les points A, O et F sont alignés ; E. aucune des propositions précédentes. Vrai.
23. On a :
A. Les points A, O et E sont alignés ; B. Les points F, O et D sont alignés vra i; C. Les points E, O et F sont alignés ;
D.Les points B, O et D sont alignés ; E. aucune des propositions précédentes.

Etude d'une fonction.
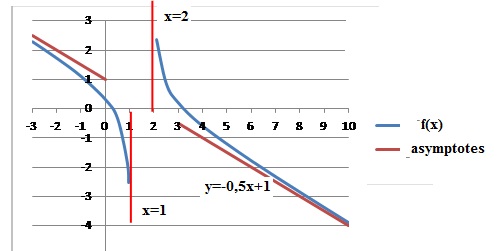
Soit la fonction numérique définie par f(x) = -0,5 x +1 +ln[(x-1) / (x-2)]

24. L'ensemble de définition de f est : :
A. ]-oo ; 1[ union ]2 ; +oo[ vrai. B. R-{ 1 ; 2}. C. ]-oo ; 1[ union ]1 ; 2[union [2 ; +oo[.
D. ]1 ; 2[. E. aucune des propositions précédentes.
(x-1) / (x-2) doit être positif avec x différent de 2 et de 1.

25. La limite en 1 de f(x) est égale à :
A. +oo . B. -oo Vrai. 0. D. 0,5. E. aucune des propositions précédentes.

26. La limite en 2 de f(x) est égale à :
A. +oo. Vrai B. -oo. C. 0. D. 0,5. E. aucune des propositions précédentes.

27. La limite en +oo de f(x) est égale à :
A. +oo. B. -oo. Vrai C. 0. D. 1. E. aucune des propositions précédentes.

28. La limite en -oo de f(x) est égale à :
A. +oo. Vrai B. -oo. C. 0. D. 1. E. aucune des propositions précédentes.

29. Sur l'intervalle ]1 ; 2 [ la fonction est :
A.strictement croissante ; B. strictement décroissante ; C. constante.
D. non définie, vrai ;E aucune des propositions précédentes.

30. Sur l'intervalle ]-oo ; 1 [ la fonction est :
A.strictement croissante ; B. strictement décroissante vrai ; C. constante.
D. non définie, ;E aucune des propositions précédentes.

31. Sur l'intervalle ]2 ; +oo [ la fonction est :
A.strictement croissante ; B. strictement décroissante vrai ; C. constante.
D. non définie, ;E aucune des propositions précédentes.

32. la courbe représentative de f admet comme asymptote, la droite d'équation :
A.x=0 ; B. x=1 vrai ; C. x=4. D. y=2 ;E aucune des propositions précédentes.

33. la courbe représentative de f admet comme asymptote, la droite d'équation :
A.y=0 ; B. y=1 ; C. x=2, vrai. D. y=2 ;E aucune des propositions précédentes.

34. la courbe représentative de f admet comme asymptote oblique, la droite d'équation :
A.y =-0,5x ; B. y = (x-2) / 2 ; C. y = -x/4. D. y=-0,5 x+1, vrai ; E aucune des propositions précédentes.

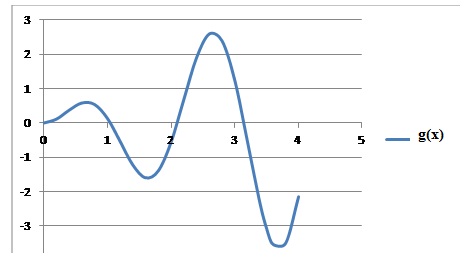
Fonction sinus et cosinus. g(x) = x sin (3x)

35. La fonction g est :
A. impaire ; B. paire vrai. C. parfois paire, parfois impaire. D. ni paire, ni impaire. E. aucune des propositions précédentes.
f(-x) = -x sin (-3x) = x sin (3x).

36. La fonction g est :
A. non périodique, vrai. B. périodique de période 2p. C. périodique de période 2p/3. D. périodique de période p/3. E. aucune des propositions précédentes.

37. La limite en +oo de g(1/x):
A. n'existe pas, B. vaut 0. vrai. C. vaut +oo. D. vaut -oo. E. aucune des propositions précédentes.
La limite de g(1 / x) quand x tend vers l'infini est égale à la limite de g(x) quand x tend vers zéro.

38. La limite de g(x) en +oo :.
A. n'existe pas, vrai. B. vaut 0. C. vaut +oo. D. vaut -oo. E. aucune des propositions précédentes.
En +oo, les maximas sont de plus en plus grands et les minimas de plus en plus négatifs.

39. La dérivée de la fonction g est :
A. cos (3x). B.x cos(3x) + sin(3x). C. cos(3x) + sin(3x).
D. cos(3x) -x sin(3x). E. aucune des propositions précédentes. Vrai.
On pose u = x et v = sin(3x) ; u' = 1 ; v' = 3 cos(3x) ; u'v+v'u = sin(3x) +3x cos(3x).

40. La primitive G de la fonction g vérifiant G(0)=0, est :
A. (-x² cos(3x) / 6.
On dérive en posant u = x² et v = cos(3x) ; u'=2x ; v' = -3sin(3x) : u'v+v'u =(2x cos(3x) -3x² sin(3x) / 6.
B. -x cos(3x) / 9 +sin(3x) / 3.
On dérive en posant u = x et v = cos(3x) ; u'=1 ; v' = -3sin(3x) : u'v+v'u =cos(3x) -3x sin(3x) ;
G' =-cos(3x) /9+x sin(3x)/3 +cos(3x).
C. -x cos(3x) / 3 +sin(3x) / 9. Vrai.
On dérive en posant u = x et v = cos(3x) ; u'=1 ; v' = -3sin(3x) : u'v+v'u =cos(3x) -3x sin(3x) ;
G' =-cos(3x)/3 +x sin(3x) +cos(3x)./3=x sin(3x)
D. x sin(3x) / 3 +cos(3x) / 9. E. aucune des propositions précédentes.

Dérivation et intégration.
41. La dérivée, sur ]-p/8 ; +p/8[ de A est :

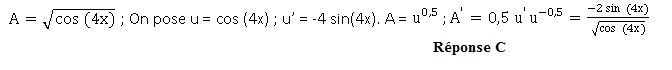
42. La valeur de l'intégrale I est :

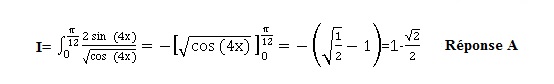
43. La valeur de l'intégrale suivante est :

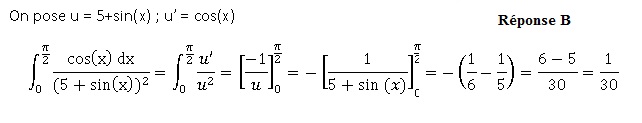
44. La valeur de l'intégrale suivante est :

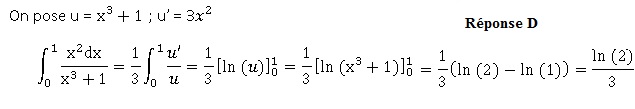
Interprétation d'une courbe.
Soit une fonction h de la forme h(x) = ax² +bx +c dont on donne une courbe représentative et où a, b, c sont des réels.

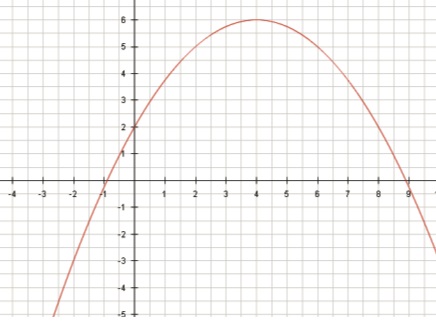
f(0 ) =2 d'où c = 2.
f(-1) = 0 : 0=a -b +2 ;
45. La tangente au point d'abscisse 4 a pour équation :
A. y=6, vrai. B. x =4. C. y = 6x+2. D. y=0. E. aucune des propositions précédentes. Vrai.
La tangente est horizontale, son coefficient directeur est nul.
La tangente passe par le point d'abscisse 4 et d'ordonnée 6 ; y =6.

46. La dérivée de la fonction h est :
A.1-x/2. B. 2-x /2. C. 0,5x-2. D. (x-4)/2 E. aucune des propositions précédentes. Vrai.
f '(x) = 2ax+b ; f '(x) est nulle pour x = 4 ; 0=8a+b ; b = -8a. f '(x) = 2a (x-4).
f(0) = c = 2 ; f(-1) =0 = a-b+2 ; 9a +2 = 0 ; a = -2/9.

47 et 48. Les ensembles de définition.et f(x) et de f '(x) sont :

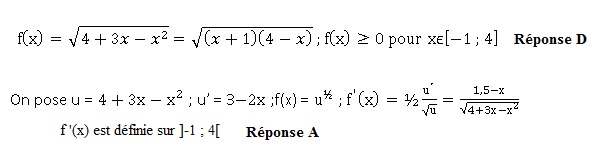
Probabilités.
Soit X une variable aléatoire suivant une loi normale centrée réduite.

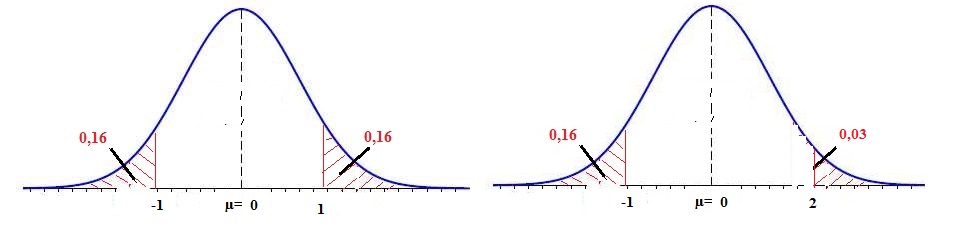
49. P(X<-1)-P(X>1) :
A. n'existe pas. B. est strictement négative. C. est strictement positive.
D. est nulle. Vrai. E. aucune des propositions précédentes.

50. P(X<-1)-P(X>2) :
A. n'existe pas. B. est strictement négative. C. est strictement positive. Vrai.
D. est nulle. E. aucune des propositions précédentes.

menu