Mathématiques,
concours EMIA
2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
1. Exprimer en fonction de a = 2n.
A = 2n+3 = 2n x23 = 8a.
B = 22n-1 =22n / 2 = (2n)2 / 2 = 0,5 a2.
C = 2-2n = 1 / 22n =1 / (2n)2 = 1/ a2.
D = 4n+1 / 21-3n =(22)n+1 / 21-3n =22n+2 / 21-3n =22n+2-1+3n=25n+1=(2n)5 x2 =2a5.
E =2n+3-22n+5x2n+1-3x2n+2=2n x23-(2n)2+5x2x2n-3x22x2n=2n (8-2n+10-12)=a(6-a).
F =(-2)2n+3=(-2)2n x(-2)3=(-2n)2x(-8) = -8a2.
G = 1 / (-2)3n-2=(-2)2-3n=(-2)2 x(-2)-3n = 4 / (-2n)3 = -4 / a3.
2. Simplifier.
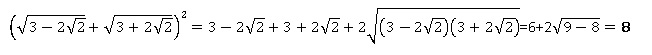
3. En utilisant la représentation trigonométrique d'un nombre complexe, simplifier au maximum les expressions suivantes :
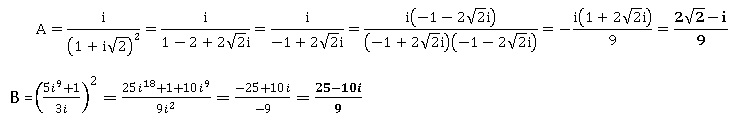
4. Résoudre dans R l'inéquation : (3x+1)2 / (3x-5) > 1.
x doit être différent de 5 /3.
(3x+1)2 > (3x-5)
Si x > 5 / 3 : 9x2+6x+1 > 3x-5.
9x2+3x+6 >0.
3x2+x+2 >0 est vérifié.
Si x < 5 / 3 : 9x2+6x+1 < 3x-5.
9x2+3x+6 <0.
3x2+x+2 < 0, impossible.
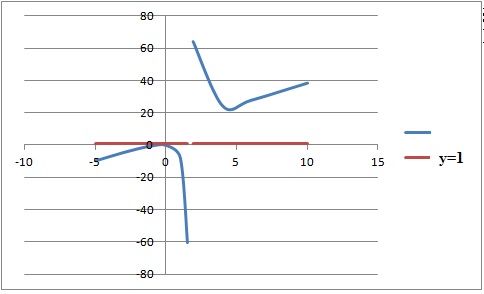 x > 5 /3. x > 5 /3.
5. Résoudre les équations logarithmiques suivantes , où log ba = lna / ln b.
A= log x32 = 5 ; ln32 / ln x = 5 ; ln x = ln (32) / 5 = 0,2 ln(32) ; x = exp(0,2 ln(25) ) = exp[ ln(25)]0,2 = (25)0,2 =25x0,2=2.
4 log2(x)=log2(x2-2)+log2(8);
4 ln(x) / ln2 =ln(x2-2) / ln 2 +ln8 / ln2.
4 ln(x) =ln(x2-2) +ln8.
ln(x4) =ln(8(x2-2)).
ln(x4)-ln(8(x2-2))=0
ln(x4 /(8(x2-2))) =0.
x4 /(8(x2-2)) =1.
x4 =8(x2-2).
x4 -8x2+16=0
(x2-4)2=0 ; x2 = 4 ; x = +2.
|
|
|
6. On considère la suite (un) définie par u0 = 1 et un+1=un exp(-un) quelque soit n entier naturel et la suite (Sn) définie par Sn = Sup pour p allant de 0 à n.
1. Montrer que un >0.
Initialisation : la propriété est vraie au rang zéro.
Hérédité : la propriété est supposée vraie au rang p. up>0.
up+1 = upexp(-up).
Or exp(-up) est positif, donc up+1 >0.
Conclusion : la propriété est vraie au rang zéro et héhéditaire, donc elle est vraie pour tout n entier naturel.
2. Montrer que la suite (un) est décroissante.
un+1 -un =un exp(-un) -un =un(exp(-un)-1)=un(1 / exp(un)-1).
un est positif ; exp(un) est positif et supérieur à l'unité.
1 / exp(un) est inférieur l à 1.
(1 / exp(un)-1) est négatif .
un+1 -un est négatif.
un+1 < un . La suite est décroissante.
3. En déduire qu'elle converge vers zéro.
La suite (un) est décroissante et minorée, donc elle converge.
Quand n tend vers l'infini :
un tend vers l.
un+1 =un exp(-un) tend vers l e-l car la fonctionf(x) = x e-x est continue en x = l.
f(l)=l ; l e-l =l ; l(e-l -1)=0 soit l = 0.
4. Montrer que pour tout entier n, un+1 = exp(-Sn).
Sn = u0 +u1 +u2 +.....+un.
On pose wn = ln un ; wn-wn+1 = ln un -ln un+1 = ln(un / un+1) = ln( exp(un)= un.
Sn = w0-w1+w1 -w2 +.....+wn-wn+1 = w0-wn+1 =ln(1)-ln(un+1)= -ln(un+1).
5. En déduire que Sn tend vers plus l'infini.
Quand n tend vers l'infini :
un tend vers zéro ;
wn= ln(un) tend vers moins l'infini ;
Sn = w0-wn+1 tend vers plus linfini.
7. .Soit f la fonction définie sur R* par f(x) = 5x / (52x-1).
1. Etudier la parité de f.
f(-x) = 5-x / (5-2x-1), multiplier numérateur et dénominateur par 52x :
f(-x) = 5x / (1-52x) = -f(x).
La fonction est impaire ; le graphe est symétrique par rapport à l'origine.
2. Montrer que pour tout x >0, f(x) = 1 / (5x-5-x).
Multiplier numérateur et dénominateur par 5-x :
f(x) = 1 / (5x-5-x).
3. Déterminer les limites de f(x) en zéro et plus l'infini.
f(x) = 1 / (exln5-e-xln5).
Quand x tend vers plus l'infini :
e-xln5 tend vers zéro ; exln5 tend vers plus l'infini ; f(x) tend vers zéro.
Quand x tend vers zéro par valeur positive :
e-xln5 tend vers 1, en retant inférieur à 1 ; exln5 tend vers 1, en restant supérieur à 1 ;
Le dénominateur tend vers zéro par valeur positive ; f(x) tend vers plus l'infini.
Quand x tend vers zéro par valeur négative :
e-xln5 tend vers 1, en retant supérieur à 1 ; exln5 tend vers 1, en restant inférieur à 1 ;
Le dénominateur tend vers zéro par valeur négaitive ; f(x) tend vers moins l'infini.
4. Calculer f '(x) et en déduire le tableau de variation de f(x).
On pose u = 5x et v = 52x-1 ; u' = ln(5) 5x ; v' =2ln(5) 52x ;
(u'v -v'u ) / v2 = [ ln(5) 5x (52x-1)-2ln(5) 53x ] / (52x-1)2.
Le signe de f '(x) est celui du numérateur :
- ln(5) 5x (52x+1).
La fonction puissance étant toujours positive, le numérateur est négatif.
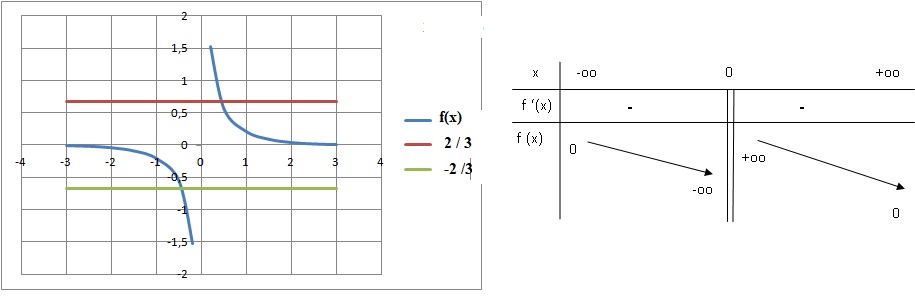
5. Résoudre f(x) = 2 / 3 et en déduire l'ensemble des solutions de f(x) = -2 / 3.
5x / (52x-1) = 2 / 3 ; 3 *5x = 2*52x-2.
On pose X = 5x positif : 2X2 -3X-2=0.
Discriminant D = 9+4*2*2 =25 ; X = (3 +5) / 4=2.
2 = 5x =exln5 ; ln2 = x ln5 ; x = ln 2 / ln 5.
Solution de x = -2/3 : par raison de symétrie, x = - ln 2 / ln 5.
|
|
|
|
8.
Une usine a besoin de deux machines M1 et M2. La probabilité que M1 tombe en panne est 0,005. La probabilité que M2 tombe en panne est 0,067. La probabilité que M2 tombe en panne sachant que M1 est en panne est 0,5.
1. Exprimer dans un langage probabiliste les données de l'énoncé.
Soient les événements suivants :
M1 : la machine M1 est en panne. P(M1) = 0,005.
M2 : la machine M2 est en panne . P(M2) = 0,0067.
PM1(M2)=0,5.
2. Quelle est la probabilité que M1 et M2 soient en panne simultanément ? En déduire la probabilité qu'une machine au moins fonctionne.
P(M1) n P(M2) =P(M1) x PM1(M2)=0,005 x0,5 =0,0025.
Probabilité qu'une machine au moins fonctionne : 1 -0,0025 = 0,9975.
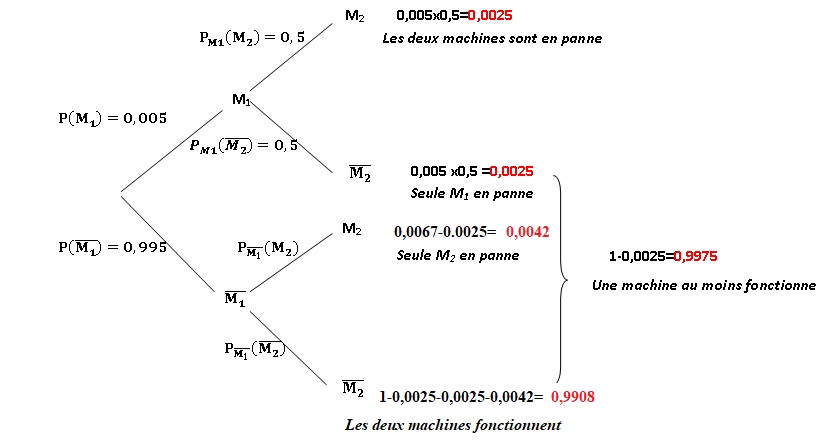
3. Quelle est la probabilité que seule M1 soit en panne ? Quelle est la probabilité que seule M2
soit en panne ? En déduire la probabilité d'avoir une seule machine en
panne. Quelle est la probabilité de n'avoir aucune machine en panne ?
Seule M1 en panne : P(M1) n P(non M2)
Seule M2 en panne : P(M2) n P(non M1)
|
R1=
|
|