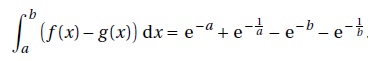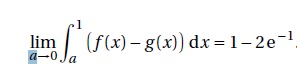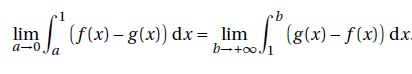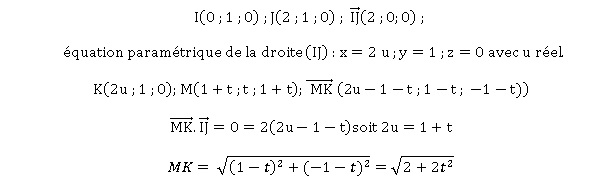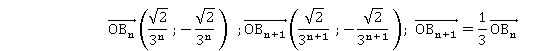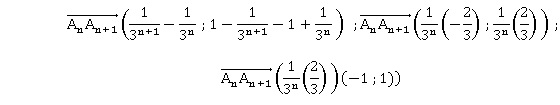Mathématiques,
bac S Nlle Calédonie 2018.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1. 6 points.
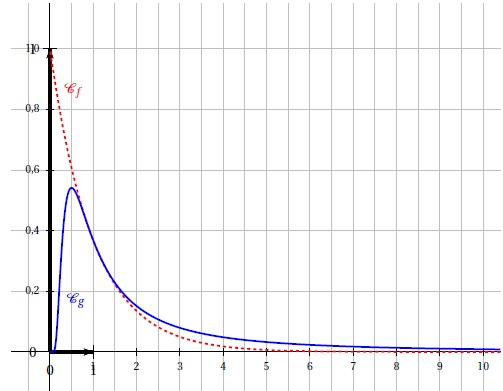
Soient f et g les fonctions définies sur ]0 ; +∞[ par f (x) = e−x et g (x) =1 / x2 e-1/x.
On admet que f et g sont dérivables sur ]0 ; +∞[. On note f ′ et g ′ leurs fonctions dérivées respectives.
Les représentations graphiques de f et g dans un repère orthogonal, nommées respectivement Cf et Cg sont données ci-dessous
Partie A – Conjectures graphiques.
Dans chacune des questions de cette partie, aucune explication n’est demandée.
1. Conjecturer graphiquement une solution de l’équation f (x) = g (x) sur ]0 ; +∞[.
Abscisse de l'intersection des deux courbes : x = 1.
2. Conjecturer graphiquement une solution de l’équation g ′(x) = 0 sur ]0 ; +∞[.
Abscisse du maximum : x = 0,5.
Partie B – Étude de la fonction g.
1. Calculer la limite de g (x) quand x tend vers +∞.
1 / x tend vers zéro ; e-1/x tend vers e0 = 1 ; 1/x2 tend vers zéro ; produit des limites g(x) tend vers zéro.
2. On admet que la fonction g est strictement positive sur ]0 ; +∞[.
Soit h la fonction définie sur ]0 ; +∞[ par h(x) = ln(g (x)).
a. Démontrer que, pour tout nombre réel x strictement positif,
h(x) =(−1−2x ln(x) ) / x.
ln(1 / x2 e-1/x)=ln(1 / x2) +ln(e-1/x) = -ln(x2) -1 /x = -2ln(x) -1 / x = (-2x ln(x)-1) / x.
b. Calculer la limite de h(x) quand x tend vers 0.
x ln(x) tend vers zéro ;(-2x ln(x)-1) tend vers -1 ; -1 / x tend vers moins l'infini.
h(x) tend vers moins l'infini quand x tend vers zéro.
c. En déduire la limite de g (x) quand x tend vers 0.
g(x) = eh(x) ; eh(x) tend vers zéro quand x tend vers zéro.
3. Démontrer que, pour tout nombre réel x strictement positif,
g ′(x) =e− 1/x (1−2x) / x4 .
On pose u = 1 /x ; u' = -1 /x2.
g(x) = u2 e-u ; on pose v = u2 et w = e-u ;
v' = 2uu' = -2/ x3 ; w' = -e-u u'= e-1/x/x2.
v' w + w' v = -2e-1/x / x3 +e-1/x / x4 =e-1/x/ x4 (1-2x)
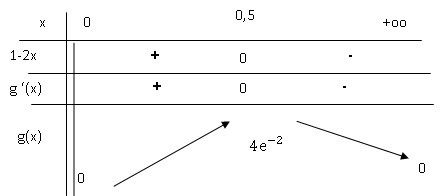
4. En déduire les variations de la fonction g sur ]0 ; +∞[.
e-1/x/ x4 est toujours positif.
Le signe de g'(x) est celui de (1-2x).
Partie C – Aire des deux domaines compris entre les courbes Cf et Cg.
1. Démontrer que la point A de coordonnées (1 ; e−1) est un point d’intersection de Cf et Cg .
On admet que ce point est l’unique point d’intersection de Cf et Cg , et que Cf est au dessus de Cg sur l’intervalle ]0 ; 1[ et en dessous sur l’intervalle ]1 ; +∞[.
e−x = 1 / x2 e-1/x ; e−x = 1 / (x2 e1/x ) ; x2 e-x e1/x = 1 ;
ln(x2) +ln(e-x) + ln(e1/x) = ln(1) = 0 ;
2ln(x) -x +1/x = 0 ; solution de cette équation x = 1 ; par suite f(1)=g(1) = e-1.
2. Soient a et b deux réels strictement positifs. Démontrer que
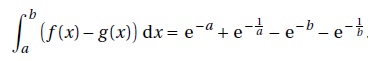
On pose u = 1 / x ; u' = -1/x2 : g(x) = -u' e-u ; primitive de g(x) :e-u =e-1/x ;
primitive de f(x) : -e-x.
Par suite : [-e-x -e-1/x]ba = -e-b -e-1/b +e-a +e-1/a.
3. Démontrer que 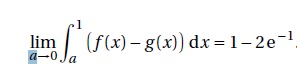
Quand a tend vers zéro : e-a tend vers 1 ; e-1/a tend vers zéro ;
Quand b est égal à 1 : -e-b = -e-1 et -e-1/b = -e-1 ;
par suite -e-b -e-1/b +e-a +e-1/a tend vers 1-2e-1.
4. On admet que
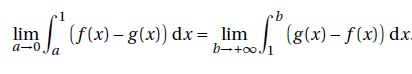
Interpréter graphiquement cette égalité.
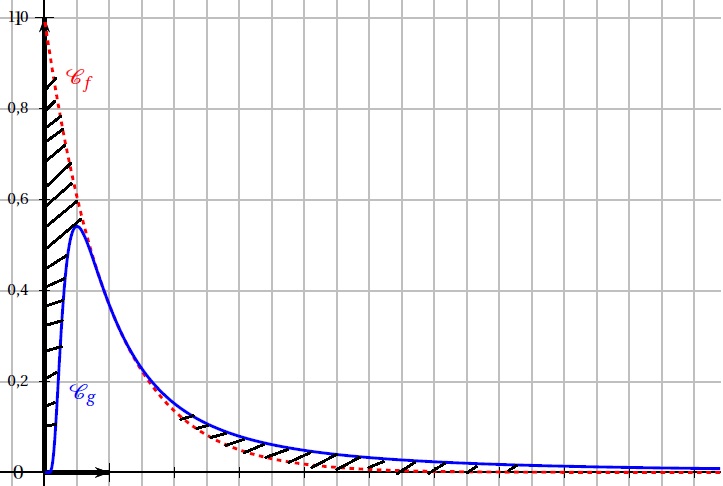
Les aires hachurées sont égales.
|
Exercice 2. 3 points.
Une
épreuve de culture générale consiste en un questionnaire à choix
multiple (QCM) de vingt questions. Pour chacune d’entre elles, le sujet
propose quatre réponses possibles, dont une seule est correcte. À
chaque question, le candidat ou la candidate doit nécessairement
choisir une seule réponse. Cette personne gagne un point par réponse
correcte et ne perd auxun point si sa réponse est fausse.
On considère trois candidats :
• Anselme répond complètement au hasard à chacune des vingt questions.
Autrement dit, pour chacune des questions, la probabilité qu’il réponde correctement est égale à 0,25
• Barbara est un peu mieux préparée. On considère que pour chacune des
vingt questions, la probabilité qu’elle réponde correctement est de 0,5.
• Camille fait encore mieux : pour chacune des questions, la probabilité qu’elle réponde correctement est de 2 /3.
1. On note X, Y et Z les variables aléatoires égales aux notes respectivement obtenues par Anselme, Barbara et Camille.
a. Quelle est la loi de probabilité suivie par la variable aléatoire X ? Justifier.
Deux issues sont possibles : réponse exacte ou réponse fausse à chaque question.
Les réponses aux questions sont indépendantes les unes des autres.
X suit la loi binomiale de paramètre n = 20 et p = 0,25.
b. À l’aide de la calculatrice, donner l’arrondi au millième de la probabilité P(X >10).
P(X >10)=1-P(X < 9) = 1-0,9860 = 0,014.
Dans la suite, on admettra que P(Y >10) ≈ 0,588 et P(Z >10) ≈ 0,962.
2. On choisit au hasard la copie d’un de ces trois candidats.
On note A, B, C et M les évènements :
• A : « la copie choisie est celle d’Anselme » ;
• B : « la copie choisie est celle de Barbara » ;
• C : « la copie choisie est celle de Camille » ;
• M : « la copie choisie obtient une note supérieure ou égale à 10 ».
On constate, après l’avoir corrigée, que la copie choisie obtient une note supérieure ou égale à 10 sur 20.
Quelle est la probabilité qu’il s’agisse de la copie de Barbara?
On donnera l’arrondi au millième de cette probabilité.
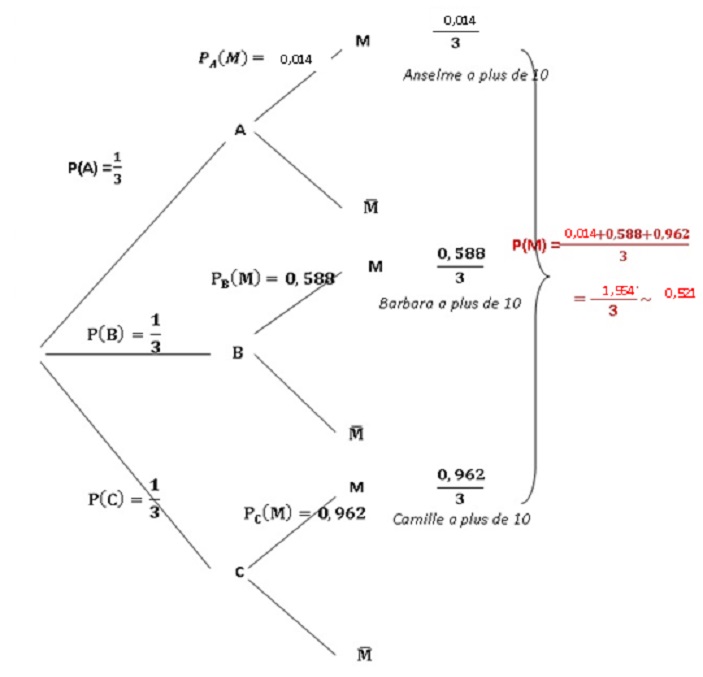
Probabilité qu'i s'agisse de la copie de Barbara : PM(B) = P(M n B) / P(M) = 0,588 / 1,564 ~ 0,376
.
|
Exercice 3. 6 points.
LorSoit ABCDEFGH le cube représenté ci-dessous.
On considère :
• I et J les milieux respectifs des segments [AD] et [BC] ;
• P le centre de la face ABFE, c’est-à-dire l’intersection des diagonales (AF) et (BE) ;
• Q le milieu du segment [FG].
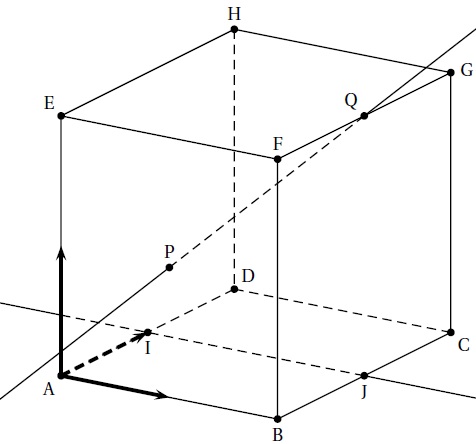
Dans tout l’exercice, on pourra utiliser les coordonnées des points de la figure sans les justifier.
On admet qu’une représentation paramétrique de la droite (IJ) est :
x = r ; y = 1 ; z = 0 , avec r réel.
1. Vérifier qu’une représentation paramétrique de la droite (PQ) est
x = 1+t ; y = t ; z = 1+t , avec t R.réel.
P( 1 ; 0 ; 1) ; Q(2 ; 1 ; 2).
Coordonnée d'un vecteur directeur de la droite (PQ) : (1 ; 1 : 1).
Représentation paramétrique de cette droite :
x = t +xP ; y = t + yP ; z = t + zP soit x = 1+t ; y = t ; z = 1+t , avec t R.réel.
Soient t un nombre réel et M(1+t ; t ; 1+t ) le point de la droite (PQ) de paramètre t .
2. a. On admet qu’il existe un unique point K appartenant à la droite (IJ) tel que (MK) soit orthogonale à (IJ).
Démontrer que les coordonnées de ce point K sont (1+t ; 1 ; 0).
b. En déduire que MK =(2+2t 2) .
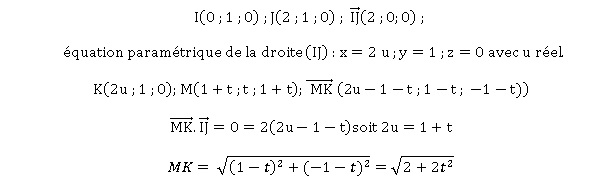
3. a. Vérifier que y −z = 0 est une équation cartésienne du plan (HGB).
Equation cartésienne de ce plan : ax +by +cz +d=0.
B(2 ;0 ; 0) appartient à ce plan : 2a+d = 0 soit d = -2a.
G(2 ; 2 ; 2) appartient à ce plan : 2a +2b +2c +d = 0 soit b = -c.
H(0 ; 2 ; 2) appartient à ce plan : 2b +2c +d = 0 doit d = 0.
Par suite : a = d = 0 ; équation cartésienne de ce plan ; by -bz = 0 soit y-z = 0.
b. On admet qu’il existe un unique point L appartenant au plan (HGB) tel que (ML) soit orthogonale à (HGB).
Vérifier que les coordonnées de ce point L sont (1+t ; 0,5 +t : 0,5 +t)
c. En déduire que la distance ML est indépendante de t.

4. Existe-t-il une valeur de t pour laquelle la distance MK est égale à la distance ML?
0,5 = 2 +2t2 ; t2 = -0,75 ; t = ±0,75½ i.
Il n'existe pas de réel t tel que la distance MK soit égale à la distance ML.
|
...
|
|
Exercice 4. 5 points.
On définit la suite de nombres complexes (zn) de la manière suivante : z0 = 1 et, pour tout entier
naturel n,
zn+1 =zn / 3 +2i / 3.
On se place dans un plan muni d’un repère orthonormé direct.
Pour tout entier naturel n, on note An le point du plan d’affixe zn.
Pour tout entier naturel n, on pose un = zn − i et on note Bn le point d’affixe un.
On note C le point d’affixe i .
1. Exprimer un+1 en fonction de un, pour tout entier naturel n.
un+1 = zn+1 -i =zn / 3 +2i / 3-i = zn/3 -i / 3 = (zn-i) / 3 = un / 3.
2. Démontrer que, pour tout entier naturel n,
un = (1 /3)n (1− i ).
u0=1-i ; un+1 = un / 3 ;
la suite (un) est géométrique de raison 1 / 3 et de premier terme 1-i.
Par suite un = (1-i)(1 / 3)n.
|
....
|
3. a. Pour tout entier naturel n, calculer, en fonction de n, le module de un.
|1-i| = (12 +(-1)2)½ = 2 ½.
Module de un : 2 ½(1 / 3)n.
b. Démontrer que la limite en plus l'infini de |zn-i| est égale à zéro.
-1 < 1 / 3 < +1, par suite (1/3)n tend vers zéro quand n tend vers plus l'infini.
c. Quelle interprétation géométrique peut-on donner de ce résultat ?
4. a. Soit n un entier naturel. déterminer un argument de un.
un / |un|= (1− i ) / 2½ = cos ( -p /4) + i sin (-p/4) = exp(-ip/4).
-p/4 est un argument de un.
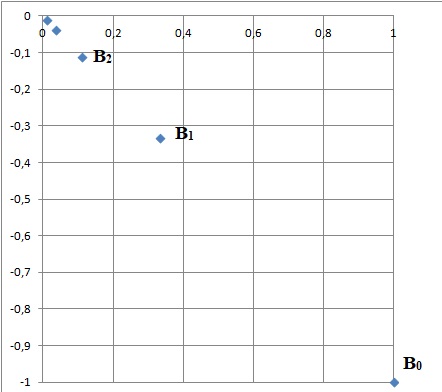
b. Démontrer que, lorsque n décrit l’ensemble des entiers naturels, les points Bn sont alignés.
un = 2 ½(1 / 3)n exp(-ip/4) : Bn( 2 ½(1 / 3)n ; - 2 ½(1 / 3)n )
un+1 = 2 ½(1 / 3)n+1 exp(-ip/4). Bn+1( 2 ½(1 / 3)n+1 ; - 2 ½(1 / 3)n+1 ).
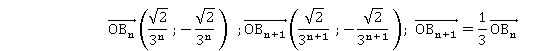
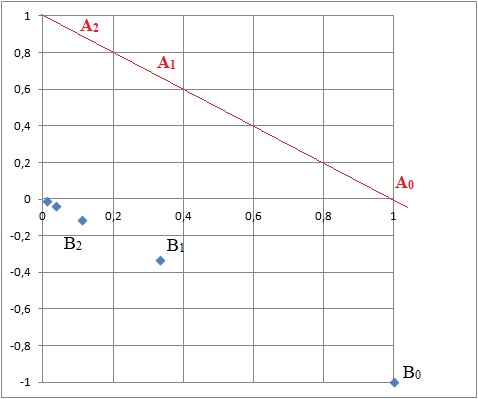
c. Démontrer que, pour tout entier naturel n, le point An appartient à la droite d’équation réduite :
y = −x +1.
A0( 1 ; 0) appartient à cette droite d'équation y = ax+b d'où b = -a
Equation de cette droite y = ax -a avec a réel.
zn = un + i ; un = (1-i)(1 / 3)n ; zn = 1 / 3n +i(1-1/3n).
zn+1 = 1 / 3n+1 +i(1-1/3n+1).
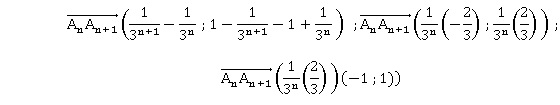
Le coefficient directeur de la droite cherchée est a = -1.
Par suite l'équation de cette droite est y = -x +1.
.
|
|