Mathématiques,
Nombres complexes, concours Puissance alpha ( Fesic)
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
|
|
Exercice 11. Suite de nombres complexes.
On se place dans le plan complexe muni d’un repère orthonormé direct et on considère la suite (zn) de nombres complexes définie, pour tout n entier, par :
z0 = 2 ; zn+1 =0,5(1+i)zn.
On pose An le point d’affixe zn et on définit, pour tout n entier, la suite (un) par un = |zn|.
a. La suite (un) est géométrique. Vrai.
Démonstration par récurrence :
Initialisation : z1 =0,5(1+i) x 2 =1+i ; u1 = (12+12)½ = 2½ ; u1 = 2½ /2 u0.
Hérédité : la propriété est supposée vraie au rang p : up+1 = 2½ /2 up.
zp+2 =0,5(1+i)zp+1 ; up+2 =0,5|1+i| up+1 =2½ /2 up+1. La propriété est vraie au rang p+1.
Conclusion : La propriété étant vraie au rang 1 et héréditaire, alors la suite est géométrique.
b. Pour tout entier naturel n,( zn+1 −zn ) / zn+1 = i. Vrai.
1- zn / zn+1 =1-2/(1+i) = (1+i-2) / (1+i)=(i-1) / (1+i)=(i-1)(1-i) / 2 =i.
c. À partir du rang n = 4, le point An appartient au disque de centre O et de rayon R =0,5. Faux.
zn+1 = 2½ /2 exp(ip/4) zn = (2½ /2)n z0 exp(in p/4). Le module de zn n'est pas constant.
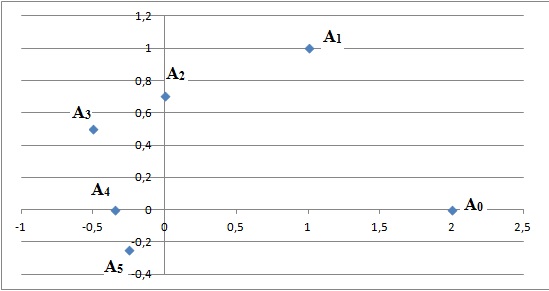
d. Pour tout entier naturel n, le triangle OAn An+1 est isocèle et rectangle. Faux.
Exercice 12. Géométrie et complexes.
Le plan complexe est muni d’un repère orthonormé direct.
On définit A et B deux points d’affixes respectives zA = 1 et zB = 2i et T la transformation complexe du plan qui, à tout point M d’affixe z non nulle, associe le point
M′ d’affixe z′ =(z −2i) / z.
a. L’image du point d’affixe exp(ip/4) par la transformation T est le point d’affixe 1+2exp(-ip/4). Faux.
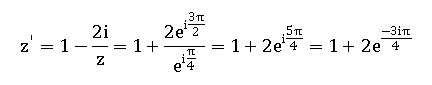
b. L’ensemble des points M du plan complexe tels que OM′ = 1 représente la médiatrice du segment [OB]. Faux.
z' = x+iy ; x2+y2=1. M' appartient au cercle centré en O, de rayon R=1.
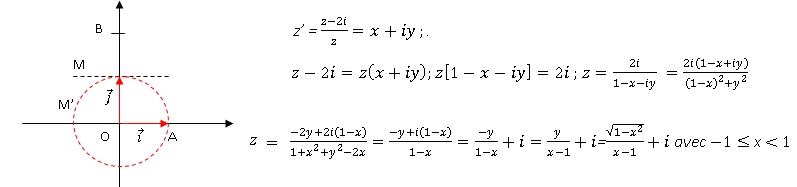
c. M′ appartient au
cercle de centre A et de rayon 1 si et seulement si le point M
appartient au cercle de centre O et de rayon R = 2. Faux.
Si M' est tel que : (x-1)2+y2 = 1, alors :
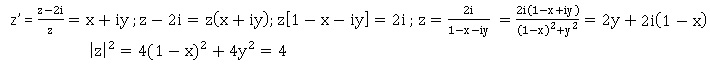
M appartient au cercle de centre O et de rayon R=2.
Réciproque : si M appartient au cercle de centre O et de rayon R = 2, alors z = x+iy avec x2+y2 = 4.
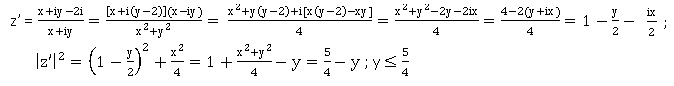
d. z′ est un nombre complexe imaginaire pur si et seulement si le point M appartient au cercle de diamètre [OB]. Vrai.
Si M appartient au cercle de diamètre [OB] : z= x+iy avec x2+(y-1)2 = 1 soit x2 +y2 =2y.
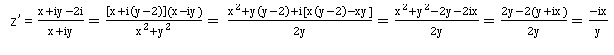
Réciproque : si z' =a i avec a réel, alors :
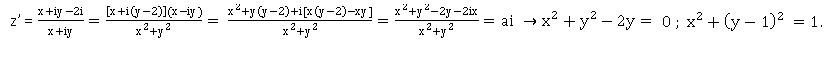 .
.
|
|
Exercice 7. Notions de
bases sur les complexes.
a : (2i)4
= -16. Faux.
24 x i2 x i2 = 16 x(-1)x(-1) = 16.
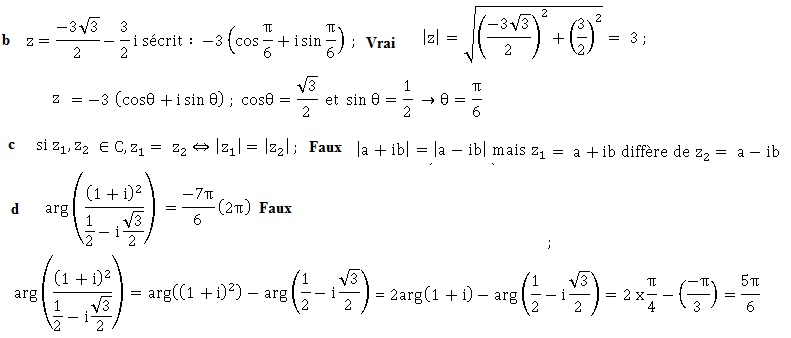
15. Nombres complexes et
géométrie.
Le plan complexe est muni d'un repère orthonormé.
On désigne par A, B , C et D les pointsd'affixes respectives : zA
= 2-3i, zB =i, zc =6-i et zD= -2 + 5i.

x ety désignent deux nombres réels, on note f ia fonction qui, à tout
point M d'affixe z = x + iy distinct de i associe le point M'
d'affixe z'.
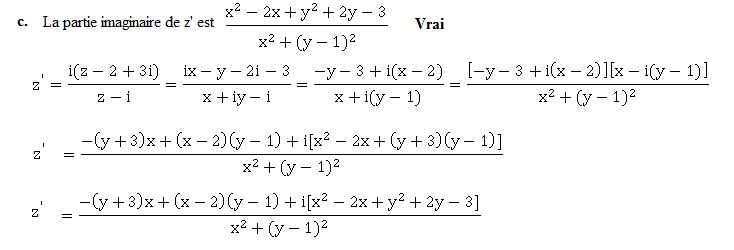
d. L'ensemble y des points M d'affixe z tels que z' soit un réel est
une droite. Faux.
La partie imaginaire de z' doit être nulle.
x2+y2-2x-2y-3=0 ; (x-1)2 +(y+1)2=5,
équation d'un cercle.
|
|
Exercice 8. Notions de base sur les complexes.
Le point A a pour affixe zA = 1+i. Soit C le cercle de centre O passant par A.
Soit B un point de C d'affixe zB positive
On définit le point E tel que le quadrilatère OBEA soit un losange.
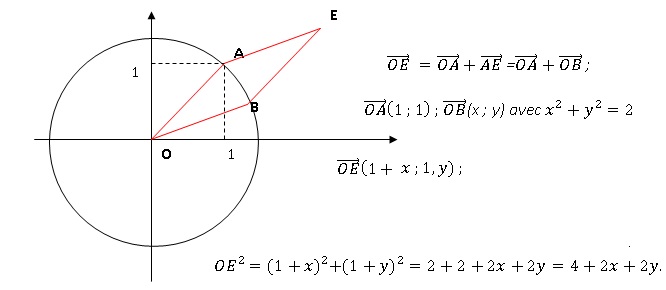
a. zA = exp(ip/4). Faux.
Module de zA : (12+12)½=2½ ; zA =2½ exp(ip/4).
b. zB = 1,5. Faux.
Le point B appartient au cercle ; son module vaut 2½.
c. zE = (1+2½)+i. Faux.
d. OE = 2 x2½. Faux.
Exercice 12. Complexes et géométrie.
Soit (E) l'équation z 2-6z+12=0.
a. (E) admet deux solutions complexes z 1 et z 2. Vrai.
Discriminant : (-6) 2 -4 x12= -12 = 12 i 2.
z 1 =(6+2 i x3 ½) / 2 = 3+i x3 ½. z 2 =(6-2 i x3 ½) / 2 = 3-i x3 ½.
Le discriminant étant négatif, (E) admet deux solutions complexes.
On pose z 1 la solution ayant une partie imaginaire positive.
b.4-z 1 = 2 exp(2i p/3). Faux.
4-z 1 =1-i x3 ½. Module de 4-z 1 : ( 1 2 +3) ½ =2.
(4-z 1 ) /2 = 0,5 -i x3 ½ / 2 =sin(5 p/6) + i cos(5 p/6) =exp(5 i p /6).
Soit A le point d'affixe z A = 4 et M 1 et M 2 les points d'affixes respectives z 1 et z 2.
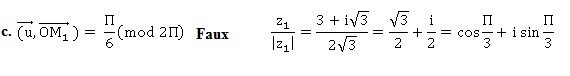 d
d. Le point M 1 est situé sur le cercle de diamètre [OA]. Vrai.
Equation de ce cercle centré au point de coordonnées (2 ; 0) : (x-2) 2 +y 2 = 4
Si M 1( 3 ;3 ½ ) appartient à ce cercle : (3-2) 2 +(3 ½) 2 = 1+3=4.
|
|