Mathématiques, bac St2S Antilles 2019

Mathématiques, bac St2S Antilles 2019.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
.

Exercice 1 ( 5 points).
Dans le cadre d’une campagne de réduction de la quantité de déchets, une enquète sur les habitudes
de compostage est menée auprès des habitants d’une ville.
Les informations recueillies ont permis d’établir que :
• 20% des personnes interrogées ont moins de 30 ans et parmi elles 30% pratiquent le compostage ;
• la moitié des personnes entre 30 et 50 ans pratiquent le compostage ;
• 35% des personnes interrogées ont plus de 50 ans et parmi elles 70% pratiquent le compostage.
On choisit au hasard une personne parmi celles interrogées. On considère les événements suivants :
J : « la personne a moins de 30 ans » ;
M : « la personne a entre 30 ans et 50 ans » ;
S : « la personne a plus de 50 ans » ;
C : « la personne pratique le compostage ».
1. En utilisant les données de l’énoncé, recopier et compléter l’arbre de probabilié ci-dessous :

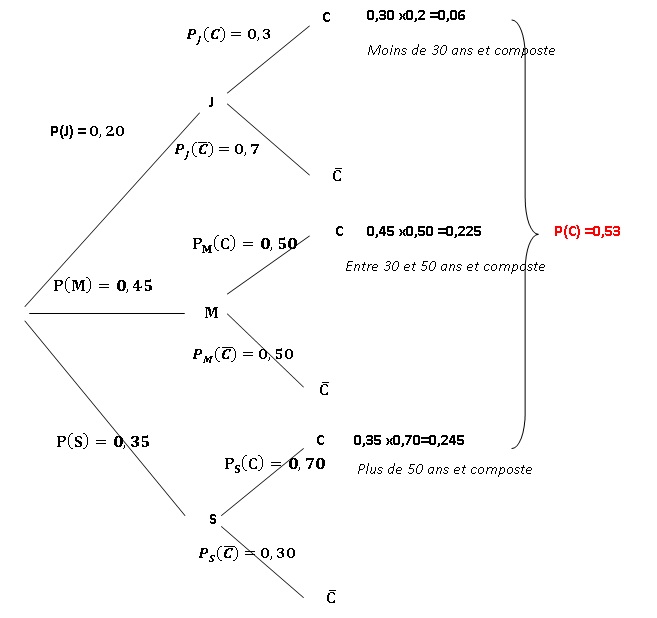
2. Définir par une phrase l’événement J n C, puis calculer sa probabilité.
La personne a moins de 30 ans et elle pratique le compostage.
P (J n C) = 0,2 x 0,3 = 0,06.
3. Calculer la probabilité de l’événement : « la personne a plus de 50 ans et pratique le compostage ».
P(S n C) = 0,35 x 0,7 =0,245.
4. Est-il vrai qu’il y a plus d’une chance sur deux que la personne choisie pratique le compostage ? Justifier.
Formule des probabilité totale :
P(C) = P (J n C) +P(S n C) +P(M n C) = 0,06 +0,245 +0,45 x 0,5 =0,53.
L'affirmation est vraie.
5. Sachant que la personne choisie pratique le compostage, quelle est la probabilité qu’elle ait plus de 50 ans ? Arrondir au centième.
P_C(S) = P(C n S) / P(C) = 0,245 / 0,53 ~0,46

Exercice 2 ( 8 points ).
La DREES a étudié l’évolution du nombre de bénéficiaires, en milliers, de l’ACTP (Allocation Compensatrice pour Tierce Personne) et de la PCH (Prestation de Compensation du Handicap), enFrance, de 2007 `a 2016.
Les deux parties de cet exercice peuvent être traitées de manière indépendante.
Partie A :
Le tableau ci-dessous donne l’évolution du nombre de bénéficiaires (en milliers) de l’ACTP de 2007 à 2016.

A
B
C
D
E
F
G
H
I
J
K

1
Année
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016

2
Rang de l'année ( x_i)
0
1
2
3
4
5
6
7
8
9

3
Nombre de bénéficiaires de l'ACTP ( y_i) en milliers
120
110
100
92
87
82
76
72
69
65

4
Taux d'évolution entre deux années ( %)

-9,1
-8,0
-5,4
-5,7
-7,3
-5,3
-4,2
-5,8

Source : DREES, direction de la recherche, des ´etudes, de l’´evaluation et des statistiques
1. Calculer le taux d’évolution du nombre de bénéficiaires de l’ACTP entre 2007 et 2008.
On donnera le résultat en pourcentage arrondi à 0, 1%.
(110-120) / 120 x100 = -8,3 %.
2. La ligne 4 est au format pourcentage arrondi à 0,1%. Quelle formule, à recopier vers la droite, peut-on saisir en C4 pour obtenir les taux d’évolution entre deux années consécutives du nombre de bénéficiaires de l’ACTP ?
=(C3-B3)/B3
3. Sur le graphique donné en annexe 1, à rendre avec la copie, représenter le nuage de points de coordonnées (x_i ; y_i) associé aux données du tableau précédent.
4. Déterminer les coordonnées du point moyen G de ce nuage de points et placer ce point G sur le graphique.
x_moyen = (0+1+2+3+4+5+6+7+8+9) / 10 =4,5.
y_moyen =(120+110+100+92+87+82+76+72+69+65) / 10 = 87,3.

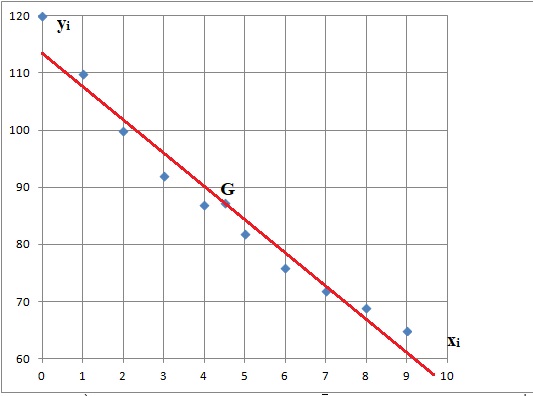
5. On décide d’ajuster ce nuage de points par la droite (D) d’équation : y = −5,9x + 113,85.
(a) Vérifier que le point G appartient à la droite (D).
y = -5,9 x4,5 +113,85 =87,3 = y_G.
(b) Tracer la droite (D) sur le graphique de l’annexe 1 en précisant les coordonnées des points utilisés.
Le point G et le point de coordonnées ( 0 ; 113,85 ).
6. En prenant cet ajustement comme modèle d’évolution jusqu’en 2019, estimer le nombre de bénéficiaires de l’ACTP en France en 2019. Préciser la démarche employée.
x = 12 ; y = -5,9 x12 +113,85 = 43,05 ~43 milliers.

Partie B :
En ce qui concerne la PCH (Prestation de Compensation du Handicap), le nombre de bénéficiaires en 2015 était de 266 000. On estime que le nombre de bénéficiaires augmente de 6% par an à partir de 2015.
Pour tout entier naturel n, on note u_n le nombre de bénéficiaires (en milliers) de la PCH, estimé selon ce modèle, pour l’année (2015+n). On a ainsi u₀ = 266.
1. Calculer les valeurs de u₁ et u₂.
u₁ = 1,06 u₀ = 1,06 x 266 =281,96.
u₂ = 1,06 u₁ = 1,06 x 281,96 =298,88.
2. Indiquer, sans justification, la nature de la suite (u_n) et préciser sa raison.
Suite géométrique de premier terme u₀ = 266 et de raison 1,06.
3. (a) Exprimer u_n en fonction de n, pour tout entier naturel n.
u_n = 266 x1,06ⁿ.
(b) En déduire une estimation, arrondie au millier, du nombre de bénéficiaires de la PCH en 2022.
n = 7 ; u₇ = 266 x1,06⁷ = 399,97.
4. Déterminer l’année à partir de laquelle le nombre de bénéficiaires de la PCH dépassera 500 000.
Préciser la démarche employée.
266 x1,06ⁿ > 500 ; 1,06ⁿ > 500 / 266 ; 1,06ⁿ >1,8797 ; n log(1,06) > log(1,8797) ; n > 10,83 : n = 11. ( année 2025 )

Exercice 3. ( 7 points )
Partie A :
On considère la fonction f définie sur l’intervalle [0 ; 16] par :
f(x) = −0,16x³+ 2,22x² − 3,7848x + 30 .
1. On note f ′ la fonction d´erivée de la fonction f.
Déterminer f ′(x) pour tout réel x de l’intervalle [0 ; 16].
f '(x) = -0,16 *3 x² +2,22*2 x-3,7848.
f '(x) = -0,48 x² +4,44 x -3,7848.
2. V´erifier que : f′(x) = (x − 8,3)(−0,48x + 0,456).
On développe : -0,48 x² +0,456 x+8,3 *0,48 x -8,3 *0,456 = -0,48 x² +4,44 x -3,7848.
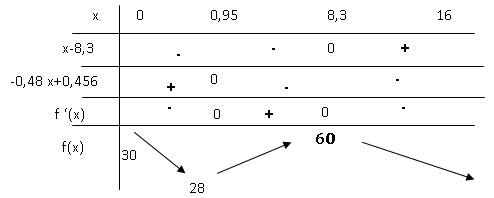
3. Compléter le tableau de l’annexe 2, à rendre avec la copie, qui donne le signe de la dérivée f ′ et les variations de f.
4. Donner le maximum de la fonction f sur [0 ; 16] (arrondi à l’unité) et la valeur pour laquelle il est atteint.

Partie B :
On s’intéresse à l’évolution de la quantité d’antigènes, d’une part, et de la quantité d’anticorps, d’autre part, présents dans le sang d’une personne contaminée par des bactéries pathogènes, dans les jours qui suivent la contamination.
On donne en annexe 2, à rendre avec la copie, les courbes représentatives de deux fonctions dans un repère du plan :
• C_fest la courbe représentative de la fonction f étudiée dans la partie A : elle représente la quantité d’antigènes présents dans le sang en UA (Unité Arbitraire) en fonction du temps (en jours) écoulé depuis la contamination.
• C_g représente la quantité d’anticorps dans le sang en UA (Unité Arbitraire) en fonction du temps (en jours) écoulé depuis la contamination.
En s’aidant du graphique de l’annexe 2, et en faisant apparaître les traits utiles à la lecture, répondre aux questions suivantes :

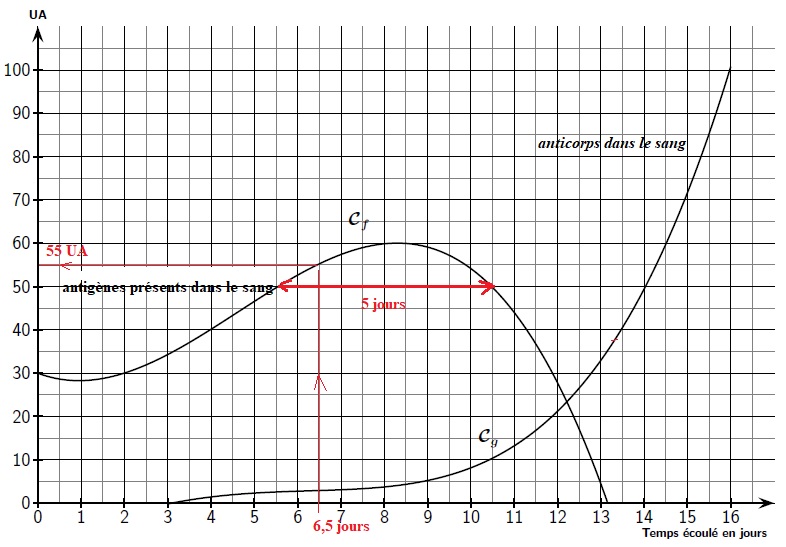
1. (a) Quelle est la quantité d’antigènes présents dans le sang 6,5 jours après la contamination ?
55 UA.
(b) Au bout de combien de temps commence la production d’anticorps ?
Au bout de 3 jours.
2. Pendant combien de temps la quantité d’antigènes dépasse-t-elle 50 UA?
5 jours.
3. Au bout de combien de temps la quantité d’antigènes est-elle maximale ? Quelle est alors cette quantité en UA?
Au bout de 8,3 jours, la quantité d'antigènes est maximale et vaut 60 UA.
4. La personne est considérée comme guérie lorsque la quantité d’anticorps présents dans le sang est supérieure à la quantité d’antigènes présents dans le sang. Au bout de combien de temps cette personne peut-elle être considérée comme guérie ?
12,3 jours.

menu