Mathématiques,
Bts chimiste 2017.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
|
......
.....
|
Exercice 1.
10 points.
Le benzène, à l'état de vapeur et dilué dans un gaz inerte, réagit avec le dichlore.
Partie A.
Dans certaines conditions, la réaction de chloration du benzène conduit
à la formation de monochlorobenzène et de dichlorobenzène.
On peut admettre que la concentration en dichlore est constante pendant
toute la durée de la réaction (car cette concentration en dichlore est
très grande par rapport à la concentration en benzène).
Nous étudierons les concentrations molaires respectives du benzène et du monochlorobenzène.
À l'instant t , exprimé en minute, on désigne par x(t ) et y(t ) les
concentrations molaires respectives du benzène et du monochlorobenzène
en mole par litre.
À l'instant t = 0 , les concentrations molaires exprimées en mol.L–1 sont égales à :
0,2 pour le benzène ; 0 pour le monochlorobenzène.
On admet que les fonctions x et y sont solutions sur [0 ; + oo[ du système différentiel (S)
x'(t) = -0,01 x(t). E1.
y'(t) = 0,01 x(t) -0,09y(t). E2.
1.a) Résoudre l'équation différentielle E1.
b) Déterminer la solution x de E1 vérifiant la condition initiale x(0) = 0,2.
x'(t) +0,01x(t) = 0 ; solution x(t) = A e-0,01t avec A une constante.
x(0) =0,2 = A ; x(t) =0,2 e-0,01t.
2.a. Montrer que l’équation E2 équivaut à l’équation différentielle E3 :
y'(t) +0,09 y(t) = 2 10-3 e-0,01t.
y'(t) + 0,09y(t) = 0,01 x(t)
y'(t) + 0,09y(t) = 0,01 x0,2e-0,01t = 2 10-3 e-0,01t.
b) Résoudre l'équation différentielle E0 : y '(t) + 0,09 y(t ) = 0 .
y(t) = B e-0,09t avec B une constante.
c) Déterminer le réel A de sorte que la fonction g définie sur [0 ; + oo[ par g(t ) = Ae -0,01 t soit une solution particulière de l'équation différentielle E3.
g'(t) = -0,01A e -0,01 t ; repport dans E3.
-0,01A e -0,01 t +0,09Ae -0,01 t =2 10-3 e-0,01t.
0,08 A = 2 10-3 ; A =0,025.
g(t ) = 0,025e -0,01 t .
d) Résoudre l'équation différentielle E3.
Solution générale de E0 + solution particulière de E3.
y(t) = B e-0,09t + 0,025 e-0,01t.
e) Déterminer la solution y de E3 vérifiant la condition initiale y(0) = 0.
0 = B +0,025 ; B = -0,025.
y(t) = -0,025 e-0,09t + 0,025 e-0,01t = 0,025(e-0,01t -e-0,09t).
Partie B.
On considère la fonction y définie sur [0 ; + oo[ par : y(t) = 0,025 (e - 0,01 t- e - 0,09 t )
1) Montrer que, pour t Î[0 ; + oo[ , la dérivée y ' de la fonction y est définie par
y '(t) = 2,5 10- 4 e- 0,01 t (9 e- 0,08 t -1) .
y'(t) = 0,025 (-0,01e-0,01t +0,09 e-0,09t).
y'(t) = 2,5 10-4(-e-0,01t +9e-0,08t e-0,01t).
y '(t) = 2,5 10- 4 e- 0,01 t (9 e- 0,08 t -1) .
2) Résoudre l'inéquation y '(t ) > 0 . En déduire les variations de y sur [0 ; +oo[.
2,5 10- 4 e- 0,01 t est positif ; y '(t ) > 0 équivaut à 9 e- 0,08 t > 1.
e- 0,08 t > 1 /9 ; -0,08t > ln(1/9) ; 0,08 t < ln(9) ; t < ln(9) / 0,08.
y(t) est croissante sur [0 ; ln(9) / 0,08 ]
y(t) est décroissante sur [ln(9) / 0,08 ; +oo].
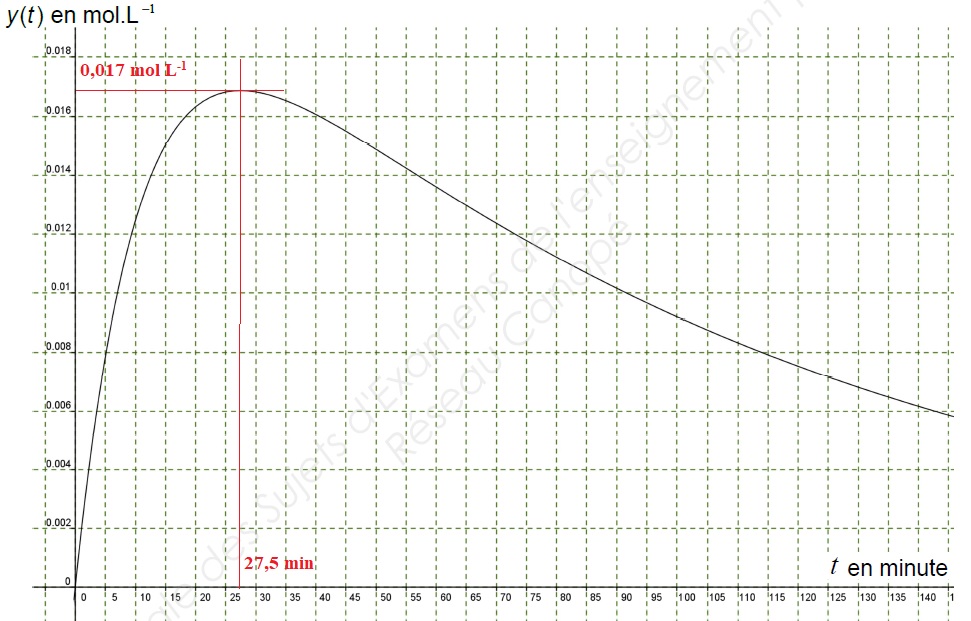
3) En déduire que la fonction y admet un maximum en un instant tm . Donner la valeur exacte de tm puis sa valeur arrondie à 10 -1.
tm = ln(9) / 0,08 ~27,5 min.
4) Vérifier graphiquement la valeur de tm sur la courbe donnée. Lire une valeur approchée du maximum obtenu à 10 -3 près.
|
...
|
|
Exercice 2 (10 points)
Partie A : Analyse d’une réaction chimique
La connaissance d’une réaction chimique que l’on ne précisera pas a
conduit au choix de trois facteurs qui semblent avoir une influence sur
le rendement de la réaction.
Pour étudier le rendement Y de cette réaction, on réalise un plan d’expériences 2 3complet, construit selon l’algorithme de Yates. On note :
· X1 la variable qui associe au facteur « proportion de soude » son niveau,
· X2 la variable qui associe au facteur « agitation » son niveau,
· X3 la variable qui associe au facteur « durée de mise en oeuvre de la réaction » son niveau.
En fonction du domaine expérimental, on attribue les niveaux suivants à chacun des facteurs :
Niveau
|
-1
|
+1
|
Proportion de soude en %
|
30
|
40
|
Agitation
|
sans agitation
|
avec agitation
|
Durée de mise en oeuvre de la réaction en minute
|
30
|
50
|
On réalise huit expériences dont les résultats sont donnés dans le tableau suivant :
Expérience
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
Proportion de soude en %
|
30
|
40
|
30
|
40
|
30
|
40
|
30
|
40
|
Agitation
|
sans
|
sans
|
avec
|
avec
|
sans
|
sans
|
avec
|
avec
|
Durée de mise en oeuvre de la réaction (min)
|
30
|
30
|
30
|
30
|
50
|
50
|
50
|
50
|
Rendement en %
|
42
|
38
|
54
|
37
|
57
|
74
|
56
|
15
|
Le modèle retenu pour le rendement Y est un modèle polynomial de la forme :
Y = a0 + a1 X1 + a2 X2 + a3 X3 + a12 X1X2 + a13 X1X3 + a23 X2X3 +a123 X1X2X3 + e.
Dans cette partie, les résultats seront arrondis à 10-3 .
1) Compléter la
matrice des expériences et des effets, puis calculer une estimation
ponctuelle de chacun des coefficients du modèle et donner l’expression
du modèle.
Expérience
|
Moyenne
|
X1
|
X2 |
X3 |
X1X2 |
X1X3 |
X2X3 |
X1X2X3 |
Y
|
1
|
1
|
-1
|
-1
|
-1
|
1
|
1
|
1
|
-1
|
42
|
2
|
1
|
1
|
-1
|
-1
|
-1
|
-1
|
1
|
1
|
38
|
3
|
1
|
-1
|
1
|
-1
|
-1
|
1
|
-1
|
1
|
54
|
4
|
1
|
1
|
1
|
-1
|
1
|
-1
|
-1
|
-1
|
37
|
5
|
1
|
-1
|
-1
|
1
|
1
|
-1
|
-1
|
1
|
57
|
6
|
1
|
1
|
-1
|
1
|
-1
|
1
|
-1
|
-1
|
74
|
7
|
1
|
-1
|
1
|
1
|
-1
|
-1
|
1
|
-1
|
56
|
8
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
15
|
Estimation es effets
|
a0 |
a1 |
a2 |
a3 |
a12 |
a13 |
a23 |
a123 |
|
a0=(42 +38 +54 +67 +57 +74 +56 +15) / 8 = 46,625.
a1 =(38 +37+74+15) / 4- 46,625 = -5,625.
a2 = (54+37+56+15)/4-46,625= -6,125.
a3 =(57 +74+56+15)/4 - 46,625= 3,875.
a12=(42+37+57+15)/4-46,625= -8,875.
a13=(42+54+74+15)/4-46,625= -0,375.
a23=(42+38+56+15)/4-46,625= -8,875.
a123=(38+54+57+15)/4-46,625= -5,625.
Y = 46,625 -5,625 X1 -6,125 X2 + 3,875 X3 -8,875 X1X2 -0,375 X1X3 -8,875 X2X3 -5,625 X1X2X3 + e.
2) a) Pour une durée de mise en oeuvre de réaction de 40 minutes, soit X3 = 0, et une proportion de soude de 30%, soit X1 = -1, est-il préférable d’agiter ou de ne pas agiter pour avoir un meilleur rendement ? Quel est alors le rendement obtenu ?
Avec agitation (X2=1) : Y = 46,625 +5,625 -6,125 + 0 +8,875 -0 -0 -0 ~45,8 %.
Sans agitation (X2=-1) : Y = 46,625 +5,625 +6,125 + 0 -8,875 -0 -0 -0 ~49,5 %. Il est préférable de ne pas agiter.
b)
Reprendre la question précédente avec toujours une durée de mise en
oeuvre de réaction de 40 minutes, mais avec une proportion de soude de
40%.
X1 = 1 ; X3 = 0.
Avec agitation (X2=1) : Y = 46,625 -5,625 -6,125 + 0 -8,875 -0 -0 -0 =26 %.
Sans agitation (X2=-1) : Y = 46,625 -5,625 +6,125 + 0 +8,875 -0 -0 -0 =56 %. Il est préférable de ne pas agiter.
|
....
|
Partie B :
Dans cette partie, les résultats seront arrondis à 10 -2 .
La saponification de l’huile de coco nécessite des pastilles de soude. Cette réaction est utilisée pour fabriquer des savons.
À l’issue de la fabrication, cinq cents savons ont été prélevés au hasard pour un contrôle de conformité.
Ces cinq cents savons prélevés constituent un échantillon dont les
masses en gramme se répartissent en 10 classes données dans le tableau
suivant :
Classes
|
[91 ; 91;1[ |
[91,1 ; 91;2[ |
[91,2 ; 91;3[ |
[91,3 ; 91;4[ |
[91,4 ; 91;5[ |
[91,5 ; 91;6[ |
[91,6 ; 91;7[ |
[91,7 ; 91;8[ |
[91,8 ; 91;9[ |
[91,9 ; 92[ |
Effectifs
|
11
|
27
|
53
|
85
|
104
|
97
|
60
|
30
|
18
|
15
|
1) Calculer une valeur approchée de la moyenne m et de l’écart type s de cette série.
Compte-tenu de l’erreur commise en supposant toutes les observations
d’une classe au centre de celle-ci, on se contentera d’une précision de
10−2.

2) Soit X la
variable aléatoire qui à tout savon associe sa masse en gramme. On
admet que X suit la loi normale de moyenne 91,48 et d’écart-type 0,20.
Calculer les probabilités suivantes : P(X ≤ 91,6) et P(91,4 ≤ X ≤ 91,7) .
P(X ≤ 91,6) =0,73.
P(X ≤ 91,4) =0,3446 ; P(X ≤ 91,7) =0,8643 ; P(91,4 ≤ X ≤ 91,7) =0,8643-0,3446 ~0,52.
3) Pour livrer les
savons à une société chargée de la distribution, on conditionne ceux-ci
sous la forme de cartons de 120 savons. Soit Y la variable aléatoire
qui à tout carton
de 120 savons associe la moyenne des masses en grammes d’un savon.
On admet que Y suit la loi normale de moyenne 91,48 et d’écart-type 0,018.
a) Déterminer le réel h arrondi à 10 -3 pour que l’on ait :
P(91,48 - h < Y < 91,48 + h) = 0,95 .
h = 1,96 x 0,018 = 0,03528 ~0,0353.
b) En déduire un
intervalle de confiance de la moyenne des masses μ au seuil de
confiance de 95 %. On donnera les résultats arrondis à 10 -3 .
[91,48 -0,0353 ; 91,48 +0,0353] soit [91,445 ; 91,515]
|
|