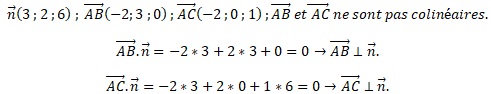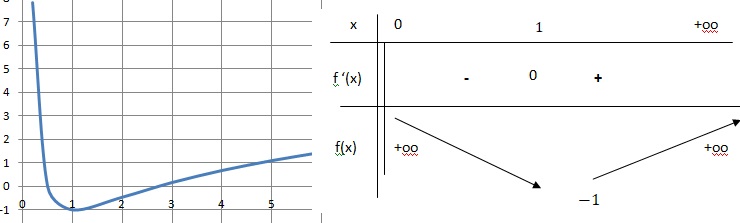Spécialité
mathématiques,
bac général 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
..
..
|
|
Exercice 1. QCM. 5 points.
Aucune justification n'est demandée ; une seule réponse est vraie.
Dans un centre de
traitement du courrier, une machine est équipée d'un lecteur optique
automatique de reconnaissance de l'adresse postale. Ce système
reconnait correctement 97% des adresses. Le reste du courrier est
qualifié d'illisible. Cette machine vient de lire 9 adresses. On note X
la variable aléatoire qui donne le nombre d'adresses illisibles parmi
ces 9 adresses. X suit la loi binomiale de paramètres n = 9 et p = 0,03.
1. La probabilité qu'aucune des 9 adresses soit illisible est égale à : 0 ; 1 ; 0,24 ; 0,76 vrai.
P(X=0) =0,76.
2. La probabilité qu'exactement 2 des 9 adresses soient illisibles pour la machine est :
p(X=2)=C92 0,032 x0,977. Réponse C.
3. La probabilité qu'au moins une des 9 adresses soit illisible est :
P(X > 1) = 1-P(X=0) ; réponse d.
Partie II.
Une urne contient 5 boules vertes et 3 boules blanches, indiscernables
au toucher. On tire au hasard et sans remise deux boules de l'urne. On
considère les événements :
V1 : la première boule tirée est verte.
B1 : la première boule tirée est blanche.
V2 : la secondee boule tirée est verte.
B2 : la seconde boule tirée est blanche.
4. La probabilité de V2 sachant que V1 est réalisée, notée PV1(V2) est égale à :
P(V1 n V2) / P(V2) =20 / 56 / ( 35 /56) = 20 / 35 = 4 /7. Réponse b.
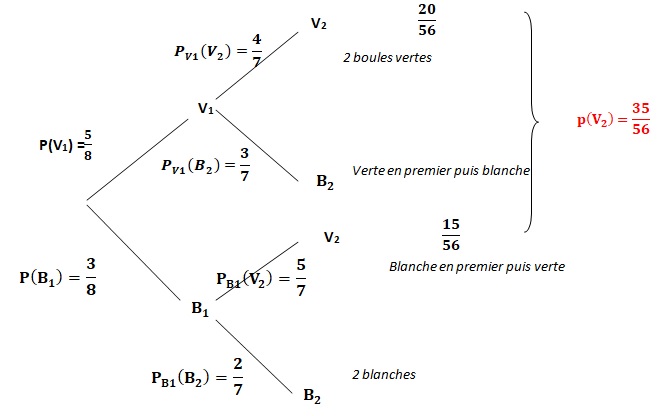
5. La probabilité de l'événement V2 est égale à :35 / 56 = 5 /8. Réponse a.
Exercice 2. 6 points.
On considère les suites (un) et (vn), strictement positives, définies par : u0 = v0 = 1 ; un+1 = un+vn ; vn+1 = 2un +vn.
1.a. Calculer u1 et v1.
u1 = u0+v0 =2 ; v1 = 2u0 +v0=3.
b. Démontrer que (vn) est strictement croissante puis en déduire que vn > 1.
vn+1 -vn = 2un >0 ; (vn) est strictement croissante.
De plus v0 = 1 ; donc vn > 1.
c. Démontrer par récurrence que un > n+1.
Initialisation : u0 = 1, la propriété est vraie au rang zéro.
Hérédité : un > n+1 est supposé vrai.
un+1 = un+vn ; or vn > 1 et un > n+1, donc un+1 > n+1+1. La propriété est vraie au rang n+1.
Conclusion : la proprièté est vraie au rang zéro et héréditaire, donc elle est vraie pour tout n entier naturel.
d. En déduire la limite de la suite (un).
un > n+1 ; quand n tend vers plus l'infini, un tend vers plus l'infini.
2. On pose rn = vn / un et on admet que : r2n = 2 +(-1)n+1 / u2n.
a. Démontrer que : -1 / u2n < (-1)n+1 / u2n < 1 / u2n.
-1 < (-1)n+1 < 1 et u2n > 0 ; donc -1 / u2n < (-1)n+1 / u2n < 1 / u2n.
b. En déduire la limite en plus l'infini de (-1)n+1 / u2n.
un > n+1 ; u2n > (n+1)2 ; 1 / u2n < 1 / (n+1)2 ; en plus l'infini la limite de 1 / u2n est zéro.
-1 / u2n > -1 / (n+1)2 ; en plus l'infini la limite de -1 / u2n est zéro.
La limite en plus l'infini de (-1)n+1 / u2n est zéro. ( d'après le théorème des gendarmes).
c. Déterminer la limite de la suite r2n et en déduire que (rn) converge vers 2½.
r2n = 2 +(-1)n+1 / u2n.
En plus l'infini, (-1)n+1 / u2n tend vers zéro ; r2n tend vers 2 et rn tend vers 2½.
d. Démontrer que pour tout entier n : rn+1 = (2+rn) / (1+rn).
rn+1 = vn+1 / un+1 = ( 2un +vn) / (un+vn).
Diviser par un numérateur et dénominateur :
rn+1 =(2+rn) / (1+rn).
e. On considère le programme écrit en langae Python :
def seuil()
n=0
r=1
while abs (r-sqrt(2)) > 10**(-4) :
r = (2+r) / (1+r)
n=n+1
return n
(abs désigne la valeur absollue, sqrt la racine carrée et 10**-4 représente 10-4).
La valeur n renvoyée est 5. A quoi correspond-elle ?
La différence entre r4 et racine carrée (2) est supérieure à 10-4.
La différence entre r5 et racine carrée (2) est inférieure à 10-4.
Exercice 3 QCM. 4 points.
On considère les points A(2 ; 0 ; 0 ), B(0 ; 3 ; 0) et C(0 ; 0 ; 1).
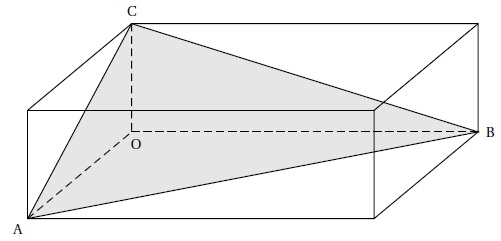
L'objectif est le calcul de l'aire du triangle ABC.
1. a. Montrer que le vecteur n de coordonnées (3 ; 2 ; 6) est normal au olan ( ABC).
1.b. En déduire qu'une équation cartésienne de ce plan est :3x+2y+6z-6=0.
Equation de ce plan : 3x +2y+6z+d = 0.
A appartient à ce plan : 3*2 +2*0 +6*0+d=0 soit d = -6.
2. On note d la droite pasant par O et orthogonale au plan (ABC).
a. Déterminer une représentation paramétrique de la droite d.
x =3t+xO =3t ; y =2t+yO =2t ; z = 6t+zO = 6 t avec t réel.
b. Montrer que la droite d coupe le plan au point H ( 18 /49 ; 12 /49 ; 36 /49).
H appartient à la droite d et au plan (ABC) :
3*3t +2*2t +6*6t-6=0 ; t = 6 /49.
xH =3*6 /49 = 18 / 49 ; yH = 2*6 /49 = 12 / 49 ; zH = 6*6/49 = 36 /49.
c. calculer la distance OH.
OH2 = (182 +122 +362) /492 =1764 /492 ; OH =42 /49.
3. En calculant de deux façons différentes le volume de la pyramide OABC, déterminer l'aire du triangle ABC.
V = aire du triangle OAB x hauteur OC / 3 = 2 x3 /2 x1 / 3 =1 cm3.
V = aire du triangle ABC x hauteur OH / 3 =1 cm3.
Aire du triangle ABC = 3/OH =3 x49 /42 =49 /14 =7/2 =3,5 cm2.
|
|
4. A. Au choix. 5 points.
Le graphique ci-dessous représente les courbes Cf et Cg des fonctions f et g définies par : f(x) = x2e-x et g(x) = e-x. 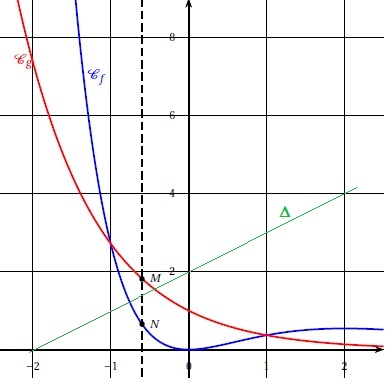
1.a Déterminer les coordonnées des points d'intersections des deux courbes.
x2e-x = e-x ; x2=1 ; x = ±1.
g(1)=e-1 et g(-1) =e.
b. Etudier la position relative des deux courbes.
f(x)-g(x) = e-x(x2-1).
f(x)-g(x) > 0 si x appartient à ]-oo ; -1[ union ]-1 ; +oo[ : Cf au dessus de Cg.
f(x)-g(x) < 0 si x appartient à ]-1 : Cg au dessus de Cf.
2. On note d(x) la distance MN. On admet que d(x) = e-x(1-x2), x appartenant à [-1 ; 1].
a. Montrer que d'(x) = e-x(x2-2x-1).
On pose u = e-x et v = 1-x2 ; u'=-e-x ; v'= -2x.
u'v+v'u= -e-x(1-x2)-2xe-x=e-x(x2-2x-1).
b. En déduire les variations de d(x).
e-x étant positif, le signe de d'(x) est celui de x2-2x-1.
Solutions de x2-2x-1=0 ; discriinant D =(-2)2+4=8 =(2*2½)2.
Solution retenenue :(2-2*2½) / 2 =1-2½.
Si x = 1-2½, d'(x) est nulle ( d(x) est minimum ).
Si x appartient à [-1 ; 1-2½[, d'(x) > 0 ; si x appartient à ] 1-2½ ; 1 [, d'(x) < 0.
c. Déterminer l'abscisse commune x0 des points M0 et N0 permettant d'obtenir une distance d minimale, et donner une valeur approchée à 0,1 près de cette distance.
d0= exp(2½-1) (1-(1-2½)2)=exp(2½-1) (-2+2*2½) ~1,3.
3. Soit D la droite d'équation y = x+2. On considère la fonction h(x) définie sur R par h(x) = e-x-x-2.
Déterminer le nombre de points d'intersection de la droite D et de la courbe Cg.
h'(x) = -e-x-1 < 0 et h(x) est strictement décroissante de +oo à -oo.
La droite D et de la courbe Cg ont un seul point commun.
Exercice B au choix.
Partie 1. Etude d'une fonction auxiliaire.
Soit la fonction g(x) définie sur ]0 ; +oo[ par g(x) =ln(x)+2x-2.
1. Déterminer les limites de g en 0 et +oo.
Quand x tend vers zéro, g(x) tend vers moins l'infini.
Quand x tend vers plus l'infini, g(x) tend vers plus l'infini.
2. Déterminer le sens de variation de g.
g'(x) = 1 /x+2 =(1+2x) / x.
g'(x) > 0 et g(x) strictement croissante.
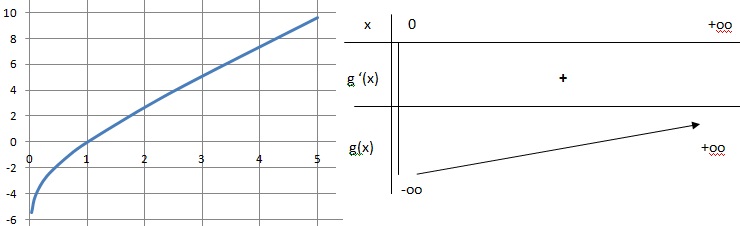
3. Démontrer que l'équation g(x) = 0 admet une seule solution a sur ]0 ; +oo[.
D'après le tableau de variation ci-dessus, g(x) = 0 admet une seule solution a sur ]0 ; +oo[.
4. Calculer g(1) puis déterminer le signe de g(x) sur ]0 ; +oo[.
g(1) = ln(1) +2-2 = 0.
Si x appartient à ]0 ; 1[ g(x) < 0 ; si x appartient à ]1 ; +oo[, g(x) > 0.
Partie 2. Etude de la fonction f définie sur ]0 ; +oo[ par f(x) =(2-1 /x)( ln(x)-1).
1.a. Démontrer que f '(x) = g(x) / x2.
On pose u = 2-1 /x et v = ln(x) -1 ; u' = 1 /x2 ; v' = 1 /x.
u'v+v'u=(ln(x)-1) / x2 +(2-1 /x) / x = (ln(x) -1 +2x-1) / x2 = g(x) / x2.
b. Dresser le tableau de variation de la fonction f.
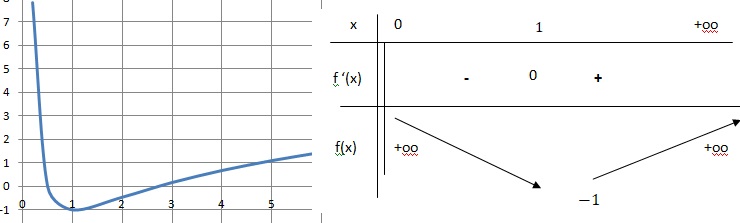
2. Résoudre l'équation f(x) = 0 puis dresser le tableau de signes de f.
(2-1 /x)( ln(x)-1) = 0
2-1 /x = 0 soit x =0,5 ; ln(x) -1 = 0 soit x = e.

Partie III. Etude d'une fonction F admettant pour dérivée la fonction f.
1. Etudier les variations de F sur ]0 ; +oo[.
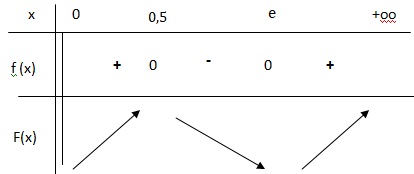
2. La courbe CF représentative de F admet-elle des tangentes parallèles à l'axe des abscisses ? Justifier.
F '(x) = f(x) s'annule pour x = 0,5 et x = e.
CF admet donc deux tangentes parallèles à l'axe des abscisses aux points d'abscisse x = 0,5 et x = e..
|
|