Mathématiques BTS groupe C Métropole Antilles 05/21.

Mathématiques BTS groupe C, Métropole Antilles 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.. ..

.
.

.. ..
......

...
Exercice 1.(10 points).
Une entreprise fabrique des charpentes en bois. Elle souhaite étudier la déformation des pièces de bois soumise à une charge constante. Le jour de l'installation, la poutre ne subit aucune déformation.
On considère la fonction f définie sur [0 ; + oo[ , représentant la déformation en mm de la poutre en fonction du temps exprimé en jour.
Partie A.
1. Expliquer pourquoi f(0) = 0.
Le jour de son installation, la poutre n'est pas déformée.
2. f est solution de l'équation différentielle (E) : 400 y' +5y = 20.
a. Résoudre l'équation (E₀) ; 400 y' +5 y = 0.
y'+0,0125 y=0
f(x) = A e^{-0,0125 t} , avec A une consatnte.
b. Déterminer une fonction constante solution de (E).
f(t) = 4.
c. En déduire l'ensemble des solutions de (E).
f(x) = A e^{-0,0125 t} +4.
d. Déterminer l'expression de la fonction f vérifiant la condition initiale f(0) = 0.
0= A e⁰+4 ; A = -4.
f(t) = 4(1-e^-0,0125t).

Partie B.
On donne la courbe représentative de la fonction f.

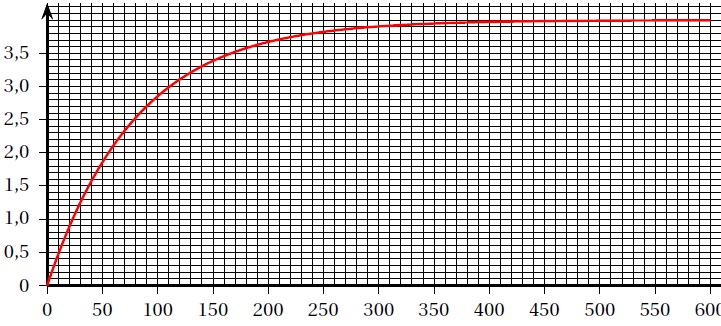
1. Déterminer la déformation au bout de 150 jours.
3,4 mm.
2. Au bout de combien de jours, la déformation atteint-elle 2 mm ?
55 jours.
3. Déterminer par le calcul la déformation limite de la poutre à long terme.
e^-0,0125t tend vers zéro et f(t) tend vers 4 mm.
La droite d'équation y = 4 est asymptote à la courbe.
4. Montrer que f '(t) = 0,05 e^-0,0125t.
f(t) = 4(1-e^-0,0125t).
f'(t)= -4 x(-0,0125) e^-0,0125t = 0,05 e^-0,0125t.
5. Etudier le sens de variation de f.
Le terme en exponentielle étant toujours positif, f '(t) >0 et f(t) est strictement croissante.
6. Déterminer par le calcul le nombre de jours à partir duquel la déformation atteint 90 % de sa valeur limite.
4 x0,9 = 4(1-e^-0,0125t).
0,9 = 1-e^-0,0125t.
e^-0,0125t=0,1.
-0,0125t = ln(0,1).
t = ln(0,1) / (-0,0125) ~184 jours.

...

....

Exercice 2. (10 points).
Partie A.
On constate deux types de défaut sur une planche : défaut de structure ( noeuds...) et défauts de rugosité de surface.
l'utilisation de planches présentant au moins un défaut est proscrite par l'entreprise.
On prélève au hasard une planche dans la production et on définit les événements suivants :
S : " défaut de structure", probabilité 0,03.
R : " défaut de rugosité", probabilité 0,05.
Ces deux événements sont indépendants.
1. Exprimer l'événement " la planche présente les deux défauts en fonction des événements R et S puis déterminer sa probabilité.
P(R n S) = p(R) x P(S) =0,03 x0,05=0,0015.
2. Décrire par une phrase l'événement non S n non R puis calculer sa probabilité.
La planche ne présente aucun défaut.
Probabilité de cet événement (1-0,03) x (1-0,05) = 0,9215.
3. Calculer la probabilité de l'événement D : "la planche présente au moins un défaut".
1-0,9215 =0,0785.
4. On choisit une planche présentant au moins un défaut ; déterminer la probabilité p qu'elle présente les deux défauts.
0,0015 / 0,0785 =0,019.

Partie B.
On admet que la probabilité qu'une planche présente au moins un défaut est 0,0785.
On prélève au hasard 15 planches dans le stock. e dernier est assez important pour que l'on puisse assimiler ce prélèvement à un tirage avec remise.
On considère la variable aléatoire X qui, à tout prélèvement , associe le nombre de planches qui présentent au moins un défaut.
1. Justifier que X suit une loi binomiale.
On choisit 15 planches de manière indépendante. Deux issues sont possibles " la planche a au moins un défaut " ou" la planche est sans défaut".
On répète 15 fois une épreuve de Bernoulli.
X suit une loi binomiale de paramètre n =15 ; p = 0,0785.
2. Déterminer la probabilité que, dans ce prélèvement, exactement 2 planches présentent au moins un défaut.
P (X =2) = 0,224.
3. Déterminer la probabilité que, dans ce prélèvement, 12 planches au moins ne présentent aucun défaut.
Au plus, 3 planches présenteront au moins un défaut.
P(X < 3) =0,974.

Partie C.
Une entreprise commande des planches de longueur 2 m.
La scierie affirme qu 94 % des planches sont conformes en longueur. On réalise un test d'hypothèse bilatéral au seuil de risque de 5 % pour vérifier cette affirmation.
Hypothèse H₀ : p = 0,94.
On appelle F la variable aléatoire qui, à tout échantillon de 100 planches prélevées au hasard dans la production, associe la fréquence des planches non conformes.
F suit la loi normale de moyenne 0,94 et d'écart type 0,0237.
1. Déterminer, sous l'hypothèse H₀, l'intervalle [m , M ] centré en 0,94 tel que p(m < F < M) = 0,95.
1,96 ( p(1-p) / 100)^½ =1,96 x(0,94 x0,06 /100)^½=0,0465.
Intervalle de confiance : [0,94-0,0465 ; 0,94 +0,0465] soit [ 0,893 ; .0,986 ].
2. Préciser l'hypothèse H₁ du test.
p diffère de 0,94.
3. Enoncer la règle de décision du test.
Si la fréquence observée appartient à [ 0,893 ; .0,986 ], H₀ est retenue , sinon H₁ est retenue.
4. Sur un échantillon de 100 poutres, 92 sont conformes en longueur. L'entreprise a -t-elle raison de douter de l'affirmation de la scierie ?
La fréquence observée f = 0,92 appartient à l'intervalle précédent.
Au risque de 5 %, l'hypothèse H₀ est retenue.
L'entreprise n'a pas raison de douter de l'affirmation de la scierie.

menu