Mathématiques.
E3C, contrôle continu première technologique
01 / 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
.
.....
|
Exercice
2.
Une
entreprise fabrique au plus 5000 lampes solaires par mois. Le résultat
mensuel, exprimé en centaines d'euros, est modélisé par une fonction b
dont la représentation graphique est donnée ci-dessous. L'axe des
abscisses indique le nombre de lampes produites et vendues exprimé en
centaines.
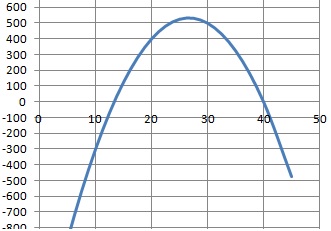
1.
Déterminer b(10) et interpréter.
b(10) = -300. En produisant et vendant 1000 lampes par mois, on perd 30 000 €.
2. La fonction b définie sur [0 ; +oo [ est définie par : b(x) = -3x2 +160x-1600.
a. Montrer que b(x) =(x-40)(-3x+40).
On développe : b(x) = -3x2+40x+120x-1600 = -3x2 +160x-1600.
b. Résoudre b(x) = 0.
x-40 = 0; x = 40.
-3x+40 = 0 ; x = 40 / 3.
c. Donner la valeur exacte du maximum de la fonction b et en quel nombre il est atteint.
x = -b / (2a) = -160 / (2 *(-3) =160 / 6 = 80 / 3 ~26,67.
b(80/3) = -3*(80 / 3)2 +160*80/3-1600 = -6400 / 3 + 12800 / 3 -4800 / 3 = (12800-6400-4800) / 3 =16 /3.
|
| .
. |
.
.
|
Exercice 3 .
On
souhaite produire une frise de tissu à partir d'un motif élémentaire A
assemblant un demi-cercle de rayon R et la moitié d'un hexagone
régulier inscrit dans un cercle de même rayon.
On donne le motif élémentaire.
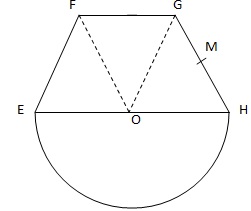
1. Le contour sera brodé. Déterminer le périmètre de ce contour sachant que R = 4 cm..
p R + 3R = 4 (3,14 +3) ~24,6 cm.
2.
L'intérieur du motif sera peint.
a. Calculer la hauteur OM du triangle OHG.
OH2 = MH2 +OM2 ; OM2 = R2 -(½R)2 =0,75 R2 = 0,75 x 42 = 12.
OM = racine carrée (12) =12½~3,46 cm.
b. déterminer l'aire de ce motif.
½pR2 + 3 xOM x R / 2 = 0,5 x3,14 x42 +3x3,46 x4 / 2 = 25,13 +20,76 =45,89 cm2.
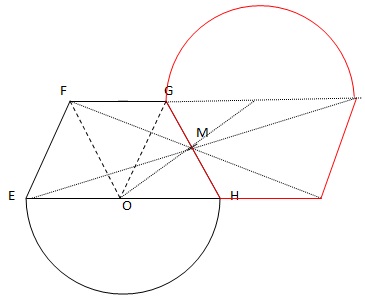
3. A partir de ce motif, construire un second motif par symétrie centrale de centre M.
4. La frise est obtenue par translation de vecteur EH à partir de ces deux motifs. Construire le prochain motif élémentaire.
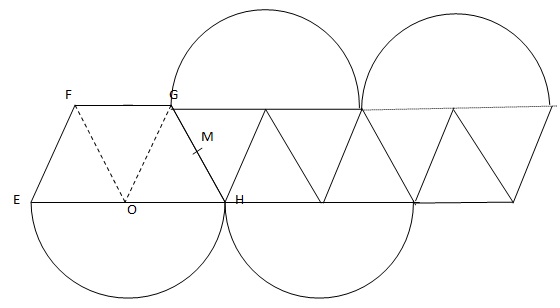
|
Exercice 4.
Un restaurant propose dans son menu trois formules :
A : entrée + plat.
B : plat + désert.
C : entrée + plat + désert.
On note le choix des clients venus pour déjeuner ( ensemble M) ou pour diner le soir ( ensemble S).
|
A
|
B
|
C
|
Total
|
Déjeuner M
|
27
|
31
|
|
75
|
Diner S
|
12
|
20
|
53
|
85
|
Total
|
39
|
51
|
70
|
160
|
1. Quel effectif doit-on écrire dans la case vide.
75-27-31=17 ou 70-53 = 17.
2.a. Calculer la fréquence en pourcentage des clients ayant choisit la formule A parmi ceux qui sont venus déjeuner le midi.
27 / 75 x100 =36 %.
b. Montrer que la fréquence en pourcentage de clients venus diner le soir parmi ceux qui ont choisi la formule B est 39,2 %.
20 / 51 x100 =39,2 %.
3. Calculer la fréquence en pourcentage des clients ayant déjeuner ce midi dans ce restaurant.
75 / 160 x100 =46,9 %.
4. Le patron
déclare : " j'ai une carte de désert très attractive car plus des trois
quart des clients choisissent une formule avec désert ". A t-il raison
? Justifier.
Formule B et formule C / total clients x 100 =(51 +70) / 160 x100 ~75,6 %, valeur supérieure à 75 %. Il a raison.
|
.
|
|