Mathématiques,
QCM, fonction, suite, probabilités, géométrie.
enseignement de spécialité première générale.
|
.
.
|
|
Sujet 53
Exercice 1.
( 5 points ).
QCM ( aucune justification n'est demandée).
1. L’équation 2𝑥2−8𝑥+6=0 admet deux solutions. Leur somme 𝑆 et leur produit 𝑃 sont :
a) S= -8 ; P =6
b) S= -4 ; P = 3
c) S=4 ; P =3. Vrai.
d) S=3 ; P=-4.
Somme S = -b / a = -(-8) / 2 = 4 ; produit P = c / a = 6 /2 = 3.
2. a est un nombre réel tel que sin(a)=0,5. On a alors :
a) sin (p-a) = 0,5. Vrai.
b) sin (p-a) = -0,5
c) sin (p-a) = 3½ /2.
d) sin (p-a) =p /6.
3. Dans un repère orthonormé du plan, on considère le cercle d’équation : (𝑥−3)2+(𝑦+0,5)2=25 / 4
On peut affirmer que :
a) ce cercle a un rayon de 6,25.
b) ce cercle passe par le point R(5 ; −2). Vrai.
c) le centre de ce cercle a pour coordonnées (−3 ; 0,5).
d) aucune des réponses a), a) ou a) n’est correcte.
Rayon du cercle : (25 /4)½ = 5 /2 = 2,5.
Coordonnées du centre du cercle (3 ; -0,5).
Si le point de coordonnées (5 ; -2) appartient au cercle, alors : (5-3)2 + (-2+0,5)2 =4+2,25=6,25 =25 / 4.
4.
Dans un repère orthonormé du plan, une équation cartésienne de la
droite passant par le point A(2 ; −4) et de vecteur normal de
coordonnées (5 ;6) est :
a). 6x-5y-32=0 ;
b) 6x+5y+8=0.
c) 5x+6y+14=0. Vrai.
d) 5x+6y-14=0.
Equation cartésienne de la droite : 5x+6y +d = 0.
A appartient à la droite : 5*2+6*(-4)+d=0 ; d = 14.
5. On considère la fonction 𝑓 définie sur 𝐑 par 𝑓(𝑥)=(2𝑥+3)e𝑥.
La fonction dérivée de la fonction 𝑓 est notée 𝑓′. On a alors :
a) 2 ex ; b) (2𝑥+3)e𝑥 ; c) (2𝑥+1)e𝑥. ; d) (2𝑥+5)e𝑥. Réponse d.
-On pose u = 2x+3 et v = ex ; u' = 2 ; v' = ex ; u'v+v'u = 2ex+(2x+3)ex =(2x+5)ex.
Sujet 54.
1. Si sin 𝑥=13 alors
A. sin (x+p) = -1 /3. Vrai.
B. sin (x-p) = 1 /3.
C. cos x = 2 /3.
D. sin (x+15 p)= 1 /3.
2. Parmi les paraboles ci-dessous laquelle représente une fonction qui n’admet aucune racine ?
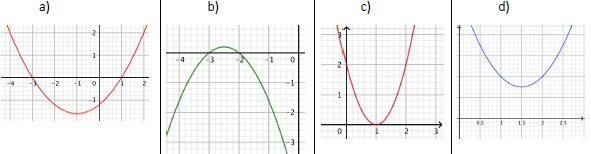 . Réponse D. . Réponse D.
3. Soit la fonction 𝑓 définie sur l’intervalle ]0;+∞[ par 𝑓(𝑥)=2𝑥− 1 / 𝑥
Le coefficient directeur de la tangente à la courbe représentative de 𝑓 au point d’abscisse 1 est :
A. 1
B. 3.
C. -1
D. 0. Réponse B.
f '(x) = 2+1/x2. f '(1) = 3.
4. Dans le plan muni d’un repère orthonormé, l’ensemble des points 𝑀(𝑥;𝑦) tels que
𝑥2−2𝑥+𝑦2+6𝑦+2=0 est :
A. une parabole
B. le cercle de centre Ω de coordonnées (−1;3) et de rayon 8.
C. le cercle de centre Ω de coordonnées (1;−3) et de rayon 2√2.
D. une droite. Réponse C.
𝑥2−2𝑥+1-1+𝑦2+6𝑦+9-9+2=0.
(x-1)2 +(y+3)2 =8 = (2 racine(2))2.
5. La loi de
probabilité d’une variable aléatoire 𝑋 donnant le gain en euros, d’un
joueur, à un jeu, est donnée par le tableau suivant :
xi
|
-10
|
6
|
10
|
P(X=xi)
|
1 /4
|
3 /8
|
3 /8
|
Sur un grand nombre de parties, le gain moyen que peut espérer le joueur est :
A. 3,5 € ; B) 4 € ; C) 2 ; D) 6 €.
-10 / 4 +6*3 /8 +10*3 /8 = -2,5 +2,25 +3,75 =3,5.
Réponse A.
|
|
Exercice 2. ( 5
points) Sujet 53. Une
entreprise fabrique des jeux en bois. Avant sa commercialisation,
chaque jeu est soumis à deux contrôles : un contrôle de peinture et un
contrôle de solidité.
Après un très grand nombre de vérifications, on constate que :
- 8 % des jeux ont un défaut de peinture,
- parmi les jeux qui n’ont pas de défaut de peinture, 5 % ont un défaut de solidité,
- 2 % des jeux présentent les deux défauts.
On choisit au hasard un jeu parmi ceux fabriqués par l’entreprise. On note :
- 𝑇 l’événement : « le jeu a un défaut de peinture. »
- 𝑆 l’événement : « le jeu a un défaut de solidité. »
1. Démontrer que 𝑃𝑇(𝑆)=0,25.
PT(S) = P(T n S) / P(T) =0,02 / 0,08 =0,25.
2. Recopier et compléter l’arbre pondéré de probabilité ci-dessous traduisant les données de l’énoncé.
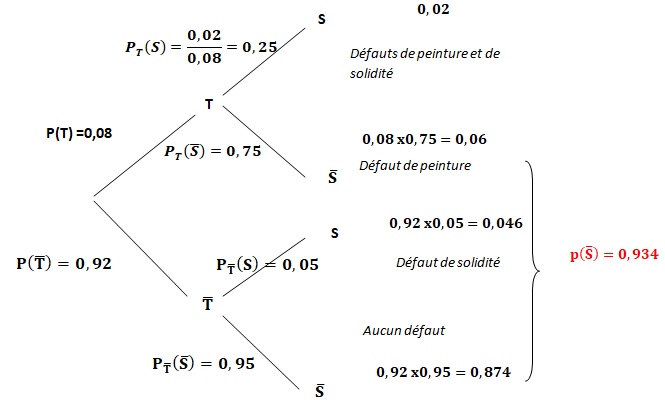
3. Démontrer que la probabilité que le jeu choisi au hasard n’ait pas de défaut de solidité est égale 0,934.
0,08 x0,75 + 0,92 x 0,95=0,06 +0,874=0,934.
4. Les jeux qui présentent un défaut de solidité sont détruits. Dans cette question, on leur attribuera un prix de vente de 0 €.
Les jeux ne présentant aucun défaut sont vendus 14 € chacun.
Les autres jeux sont vendus 9 € chacun.
On note 𝑋 la variable aléatoire qui donne le prix de vente, en euros, d’un jeu.
a. Recopier et compléter le tableau ci-dessous donnant, pour chaque valeur 𝑥𝑖 de 𝑋, la probabilité de l’événement {𝑋=𝑥𝑖}.
xi
|
0
|
9
|
14
|
P(X=xi)
|
0,066
|
0,06
|
0,874
|
b. Quel est le prix de vente moyen d’un jeu fabriqué par cette entreprise ?
On arrondira le résultat au centime d’euro.
9 x0,06 +14 x0,874 =0,54 +12,236 ~12,78 €.
Sujet 54.
Le directeur d’une maternité en milieu rural a enregistré 900 accouchements entre le 1er janvier 2019 et le 31 décembre 2019.
Depuis déjà 10 ans, il constate que le nombre d’accouchements baisse
d’environ 4 % chaque année par rapport à l’année précédente.
En supposant que cette diminution se poursuive avec ce même taux les
prochaines années, il modélise le nombre d’accouchements de cette
maternité pour l’année 2019+𝑛 à l’aide du 𝑛-ième terme d’une suite (𝑢𝑛). Il a ainsi 𝑢0=900.
1. Montrer que la suite (𝑢𝑛) est une suite géométrique dont on précisera la raison.
un+1 = (1-0,04) un = 0,96 un ; un+1 / un = 0,96. Suite géométrique de raison 0,96.
2. On considère la fonction Suite définie ci-dessous en langage Python.
def Suite(n)
u =900
for i in range(1 ; n+1):
u=0,96*u
return u
Quelle sera la valeur obtenue pour Suite(5) ?
u5 = 900 *0,965 ~734.
3. Pour tout entier naturel 𝑛, exprimer 𝑢𝑛 en fonction de 𝑛.
un = 900 *0,96n.
4. Le directeur sait que la maternité devra fermer dès le nombre d’accouchements deviendra inférieur à 600.
Avec ce modèle, la maternité sera-t-elle fermée en 2030 ? Justifier.
n = 11 ; u11=900 *0,9611 ~574. Cette valeur étant inférieure à 600, la maternité sera ferme en 2030.
5. Selon ce modèle, en quelle année la maternité fermera-t-elle ses portes ?
u10 =900 *0,9610 ~598.
u9 =900 *0,969 ~623.
La maternité fermera en 2029.
|
|
Exercice 3. ( 5 points).
Sujet 53.
L’évolution
d’une population de bactéries dépend de l’environnement dans lequel ces
bactéries sont placées. Cette population peut être modélisée par la
suite (𝑃𝑛) définie, pour tout entier naturel 𝑛, par : 𝑃𝑛+1=(1+𝛼)𝑃𝑛+𝛽, où 𝛼 et 𝛽 sont des paramètres liés à l’environnement, notamment à la température et à l’humidité.
𝑃𝑛 modélise alors le nombre de bactéries, en milliers, qui
composent cette population 𝑛 jours après les avoir introduites dans un
certain environnement.
1. Une population, initialement composée de 500 mille bactéries, est étudiée dans un environnement pour lequel 𝛼=0,2 et 𝛽=70.
a. Combien y a-t-il de bactéries dans cet environnement au bout de deux jours ?
P1 = (1+0,2)x500+70=670.
P2 = (1+0,2)x670+70=874 mille.
b.
Recopier et compléter le programme suivant, écrit en langage Python,
pour que la fonction Nombrebacteries renvoie le nombre de bactéries
présentes dans cet environnement au bout de N jours.
def Nombrebactéries(N)
P=500
for i in range (0,N)
P=P*1,2+70
return P
2. Une autre
population, initialement composée de 500 mille bactéries, est étudiée
dans un nouvel environnement. On constate que le nombre de bactéries de
cette population augmente de 9 % par jour.
a. Déterminer les valeurs des paramètres 𝛼 et 𝛽 pour cet environnement.
Pn+1 = (1+0,09) Pn ; a = 0,09 et ß = 0.
b. Quelle est, dans ce cas, la nature de la suite (𝑃𝑛) ?
Pn+1 / Pn = 1,09, suite géométrique de raison 1,09.
c. Justifier qu’après 9 jours dans cet environnement, le nombre de bactéries de cette a doublé.
P9 = 500 x1,099 ~1086 mille..
Sujet 54.
Soit la fonction 𝑓 définie sur [0 ;3] par 𝑓(𝑥)=4𝑥e−𝑥.
1. On a tracé ci-dessous la courbe représentative de la fonction 𝑓 dans un repère orthonormé d’origine 0.
Conjecturer une valeur approchée du maximum de 𝑓 sur [0 ;3].
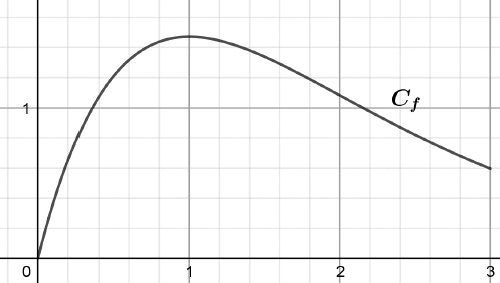
Valeur approchée du maximum de f : 1,45.
2. La fonction 𝑓 est dérivable sur [0 ;3]. Montrer que pour tout réel 𝑥 de l’intervalle [0;3], 𝑓′(𝑥)=4(1−𝑥)e−𝑥.
On pose u = 4x et v = e-x ; u' = 4 ; v' = -e-x.
u'v+v'u =4e-x -4xe-x=4(1−𝑥)e−𝑥.
3. En déduire le tableau de signes de 𝑓’(𝑥) sur [0 ;3].
4. En déduire le tableau des variations de 𝑓 sur [0 ;3] puis la valeur exacte du maximum de 𝑓 sur [0 ;3].
Le terme en exponentielle étant positif, le signe de f '(x) est celui de 1-x.
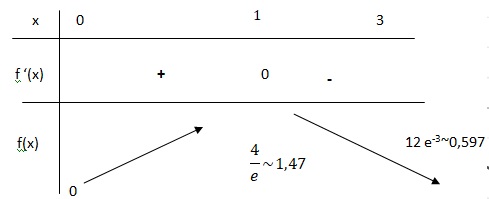
5. Soit A le point d’abscisse 1 de 𝐶𝑓 et soit t la tangente à 𝐶𝑓 au point d’abscisse 0,5. Qui, de la droite (A0) ou de la droite t, a le plus grand coefficient directeur ? Justifier.
Coefficient direxteur de la droite A0 : f(1) / 1 ~1,47.
Coefficient directeur de la droite t : f '(0,5) =4(1-0,5)e-0,5 ~1,21.
La droite AO a le plus grand coefficient directeur.
|
|
Exercice 4. ( 5 points) Sujet 53. On considère la fonction 𝑓 définie sur l’intervalle [0 ;+∞[ par 𝑓(𝑥)=3𝑥e−0,4𝑥.
La fonction dérivée de la fonction 𝑓 est notée 𝑓′.
On admet que la fonction 𝑓′ a pour expression 𝑓′(𝑥)=(−1,2𝑥+3)e−0,4𝑥.
1. Déterminer le signe de 𝑓′(𝑥) sur l’intervalle [0 ;+∞[.
Le terme en exponentielle est positif.
f '(x) a le signe de -1,2x+3.
f '(x) =0 si x = 2,5 ; f '(x) > 0 si x appartient à [0 ; 2,5 ] ; f '(x) < 0 si x > 2,5.
2. En déduire le tableau de variation de la fonction 𝑓 sur l’intervalle [0 ;+∞[.
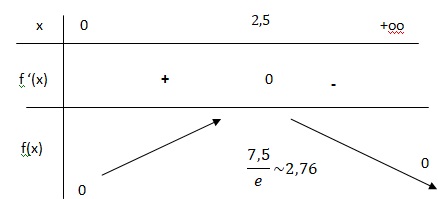
3. Un sportif a
pris un produit dopant. La fonction 𝑓 modélise la quantité, en mg/L,
de ce produit dopant présent dans le sang du sportif 𝑥 heures après la
prise.
a. Pourquoi peut-on affirmer que ce produit dopant n’est pas naturellement présent dans l’organisme du sportif ?
Initialement, la quantité présente dans le sang est nulle.
b. Combien de temps après son absorption, ce produit dopant sera-t-il présent en quantité maximale dans le sang du sportif ?
t = 2,5 heures.
c. Le sportif absorbe ce produit dopant au début d’une séance d’entraînement.
Le même jour, 6 heures après le début de cette séance d’entraînement,
il est soumis à un contrôle anti-dopage. Celui-ci se révèlera positif
si la quantité de produit dopant présent dans l’organisme de ce sportif
dépasse 1,4 mg/L. Ce contrôle anti-dopage sera-t-il positif ? Justifier.
f(6)=3*6 e-2,4 ~1,6 mg / L.
Cette valeur étant supérieure à 1,4 mg / L, le contrôle est positif.
|
Sujet 54.
150 élèves d’un établissement sont inscrits aux activités du midi :
• 30 sont inscrits en musique.
• 45 sont inscrits en sport.
• 75 sont inscrits en cinéma.
Chaque élève pratique une et une seule activité. Parmi les élèves
inscrits en musique, 30 % sont des filles. Parmi les élèves inscrits en
sport, 60 % sont des filles. Parmi les élèves inscrits en cinéma, 72 %
sont des filles.
On choisit au hasard un élève inscrit aux activités du midi.
On note : F l’événement : « l’élève choisi est une fille », M
l’événement : « l’élève choisi est inscrit en musique », S l’événement
: « l’élève choisi est inscrit en sport », C l’événement : « l’élève
choisi est inscrit en cinéma ».
1. Recopier et compléter l’arbre pondéré représentant la situation.
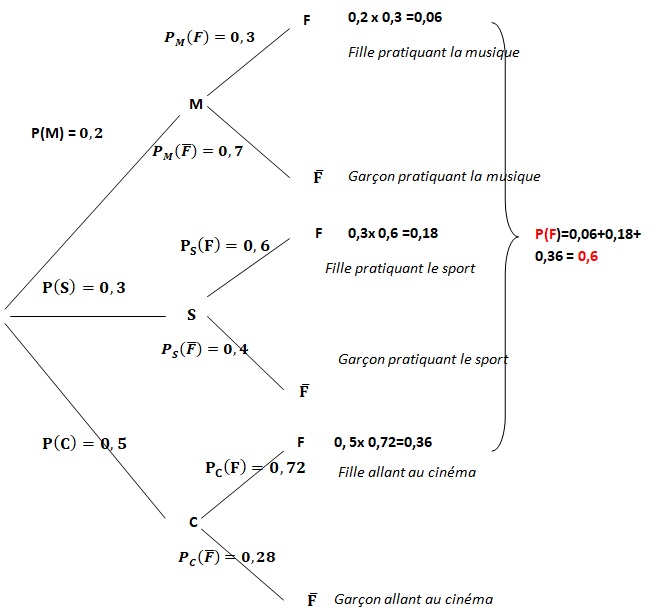
2. Calculer la probabilité que l’élève choisi soit une fille inscrite en musique.
0,2 x0,3 = 0,06.
3. Montrer que la probabilité que l’élève choisi soit une fille est égale à 0,6.
P(F) = 0,2*0,3 +0,3*0,6 +0,5*0,72 = 0,6.
4. Les évènements M et F sont-ils indépendants ?
P(M) =0,2 ; P(F) = 0,6 ; P(M n F) =0,06 différent de 0,2 *0,6.
Les évènements M et F ne sont pas indépendants.
5. Sachant que l’élève choisi est un garçon, calculer la probabilité qu’il soit inscrit en cinéma.
P(non F) =1-0,6 = 0,4 ; Pnon F(C) =P(non F n C) / P(non F) =0,5 *0,28 / 0,4 =0,35.
|
|