Spécialité
Mathématiques, classe de première 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
.
|
|
Exercice 1. QCM.
1. Pour x pièces produites, le coût de fabrication c(x), en milliers d'euros est donné par C(x) = 0,01x3-0,135x2+0,6x+15 avec x appartenant à [0 ; 30]. Pour deux pièces produites, le coût de fabrication en euros est : 15,74 ; 157,4 ; 1574 ; 15 740 vrai.
C(2) =0,01*23-0,135*22+0,6*2+15 =15,74 milliers d'euros = 15 740 €.
2. f(x) = ax2+bx+c, où a, b et c sont des réels. On donne la courbe C représentative de f et on suppose qu'elle admet l'axe des abscisses comme tangente en un de ses points.
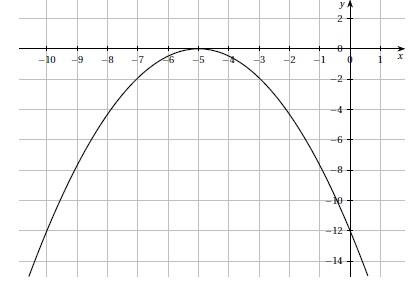
On peut affirmer que :
a < 0 et D < 0 ; a > 0 et D = 0 ; a < 0 et D = 0 vrai ; a < 0 et D > 0.
La parabole possède un maximum, donc a < 0 ; la courbe est tangente à l'axe des abscisses, donc le discriminant D est nul.
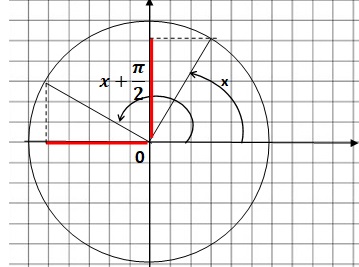
3. cos (x+p/2) est égal à :
cos(x)-sin(x) ; cos (x-p/2) ; sin(x) ; - sin(x) vrai.
4.
Dans le plan rapporté à un repère orthonormé, on donne les points A(-7
; 4) et B(1 ; -2). Le cercle de diamètre [AB) admet comme équation :
(x+7)2+(y-4)2 = 100 ; (x+3)2+(y-1)2 = 25 vrai ; (x+3)2+(y-1)2 = 100 ; (x+7)2+(y-4)2 = 25.
AB2 = (xB-xA)2 +(yB-yA)2 =82+62=100.
Le carré du rayon du cercle vaut R2 = AB2 /4 = 25.
Coordonnées du centre du cercle ( milieu de [AB]) : (xB+xA) / 2 = -3 ; (yB+yA) / 2 = 1.
5.
Dans le plan rapporté à un repère orthonormé, les droites d et d'
d'équations cartésiennes respectives 3x+2y-1 et 6x+4y+2=0 sont :
sécantes et non perpendiculaires ; confondues ; strictement parallèles, vrai ; perpendiculaires.
Coordonnées du vecteur directeur de la droite d : (3 ; 1).
Coordonnées du vecteur directeur de la droite d : (6 ; 2).
Ces deux vecteurs étant proportionnels, les droites sont parallèles.
A( 0 ; ½) appartient à la droite d.
6 xA +4yA+2 =2+2=4 différe de zéro : les deux droites ne sont pas confondues.
Exercice 2.
Une
collectivité octroie 116 610 € pour le forage d'une nappe d'eau. Le
forage du premier mètre coûte 130 € ; le forage du deuxième mètre coûte
52 € de plus que celui du premier ; le forage du troisème mètre coûte 52 € de plus que celui du premier , etc.
Le forage de chaque mètre supplémentaire coûte 52 € de plus que celui du précédent.
On note un le coût du forage du nième mètre et Sn le coût du forage de n mètres.. Ainsi u1 = 130.
1. Calculer u2 et u3.
u2 = u1 +52 =130 +52 =182.
u3 = u2 +52 =182 +52 =234.
2. Préciser la nature de la suite et exprimer un en fonction de n.
Suite arithmétique de premier terme u1 et de raidon 52.
un = u1 +52(n-1) = 130 +52(n-1).
3. Calculer S2 puis S3.
S2 = u1+u2 = 130 +182 =312.
S3 = S2+u3 = 312 +234 =546.
4.
Afin de déterminer le nombre maximal de mètres que l'entreprise peut
forer on considère la fonction Python suivante. Compléter cet
algorithme. Justifier.

C représente le coût du forage.
Sn+1 = Sn + un+1=130 +52 n.
A chaque tour de boucle on ajoute 130 + 52n à C.
5. On admet que Sn = 26n2+104n. En déduire la valeur de n renvoyée par ce programme.
26n2+104n < 116 610.
On résout l'équation : 26n2+104n -116 610 =0.
Discriminant D =1042 +4 *26*116610=12 138 256=34842.
La solution positive est retenue : (-104 +3484) / (2*26)=65.
|
Exercice 3.
On
lance deux dés cubique équilibrés classiques et on note les
numéros apparaissant sur la face supérieure de chaque dé. Soit X la
variable aléatoire égale au produit des numéros apparaissant sur les
deux faces. Le jeu est gagné si ce produit est strictement inférieur à
10.
1.a Donner les valeurs prises par la variable aléatoire.
|
1
|
2
|
2
|
3
|
3
|
4
|
1
|
1
|
2
|
3
|
4
|
5
|
6
|
2
|
2
|
4
|
6
|
8
|
10
|
12
|
3
|
3
|
6
|
9
|
12
|
15
|
18
|
4
|
4
|
8
|
12
|
16
|
20
|
24
|
5
|
5
|
10
|
15
|
20
|
25
|
30
|
6
|
6
|
12
|
18
|
24
|
30
|
36
|
1.b. Déterminer la loi de probabilité de X.
valeur de X
|
1
|
2
|
3
|
4
|
5
|
6
|
8
|
9
|
10
|
12
|
15
|
16
|
18
|
20
|
24
|
25
|
30
|
36
|
probabilité P(X)
|
1 / 36
|
1/18
|
1/18
|
1/12
|
1/18
|
1/9
|
1/18
|
1/36
|
1/18
|
1/9
|
1/18
|
1/18
|
1/18
|
1/18
|
1/18
|
1/36
|
1/18
|
1/36
|
1.c. Déterminer la probabilité de gagner : P(X <10)= 2*1 /36 +4 *1 /18 +1 /12 +1/ 9 =17 /36
2. On
lance à présent des dés spéciaux : ce sont des dés cubiques équilibrés
dont les faces sont numérotés différemment des dés classiques.
Premier dé : 1, 2, 2, 3, 3, 4 ; second dé :1, 3, 4, 5 ,6, 8.
On note Y la variable aléatoire égale au produit des numéros
apparaissant sur les deux faces après lancer de ces deux dés spéciaux.
Déterminer P(Y < 10).
.
|
1
|
2
|
2
|
3
|
3
|
4
|
1
|
1
|
2
|
2
|
3
|
3
|
4
|
3
|
3
|
6
|
6
|
9
|
9
|
12
|
4
|
4
|
8
|
8
|
12
|
12
|
16
|
5
|
5
|
10
|
10
|
15
|
15
|
20
|
6
|
6
|
12
|
12
|
18
|
18
|
24
|
8
|
8
|
16
|
16
|
24
|
24
|
32
|
Il y a 17 possibilités de gain sur 36 possibles.
3. Avec quels dés est-il préférable de jouer ?
Peu importe, les deux types de dés conduisent à la même probabilité de gain.
Exercice 4.
Soit la fonction définie sur R par : f(x) = e2x+6ex-8x-4. On note C sa courbe représentative.
Soit D la droite d'équation cartésienne : y =-8x-4.
1. Montrer que f '(x) =2(ex-1)(ex+4).
f '(x)=2e2x+6ex-8 = 2( e2x+3ex-4) ;
(ex-1)(ex+4)=e2x+4ex-ex-4 = e2x+3ex-4.
2. Etudier le signe de f '(x).
ex+4 > 0 ; la dérivée est du signe de ex-1 ;
si x < 0, ex-1 < 0 ; si x > 0, ex-1 >0 ; si x=0, f '(x) = 0.
3. Dresser le tableau de variation de f(x) sur R.
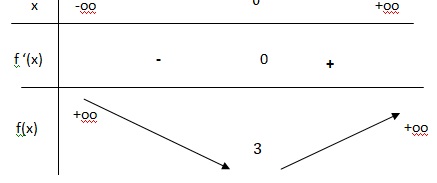
4. En déduire le signe de f(x) sur R.
f(x) est admet un minimum égal à 3 : f(x) est donc strictement positif sur R.
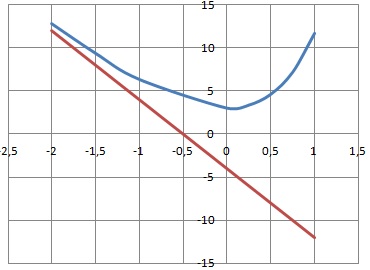
5. La courbe C et le droite D ont-elles un point commun ? Justifier.
Si la courbe C et la droite D se coupent en un point alors : e2x+6ex-8x-4 =-8x-4.
e2x+6ex=0 ; ex(ex+6) =0.
Or ex > 0, donc ex(ex+6) n'est jamais nul.
La courbe C et le droite D n'ont pas de point commun.
|
|




