Rafraichir une boisson, bac Liban 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... On s'intéresse à l'évolution de la température  T du système ( canette + boisson) placé dans un congelateur dont l'air intérieur est assimilé à un thermostat 1. Exprimer la variation d'énergie interne dU système entre l'état initial à la température qi et l'état final à la température qf. On note C=1,50 103 J K-1 la capacité thermique du système. DU = Q = C (qf- qi ). 2. Calculer cette variation si le système se rfroidit de la température ambiante (25°C) à 5°C. DU =1,50 103 ( 5-25)= -3,0 104 J. 3. Commenter le signe du résultat et interpréter celui-ci en termes d'énergie microscopique. Le système cède de l'énergie au milieu extérieur. L'agitation des atomes et molécules constituant le système diminue. Au cours d'une expérience on mesure la température à l'intérieur de la canette en fonction du temps. 4. Déterminer graphiquement la durée nécessaire à ce refroidissement. 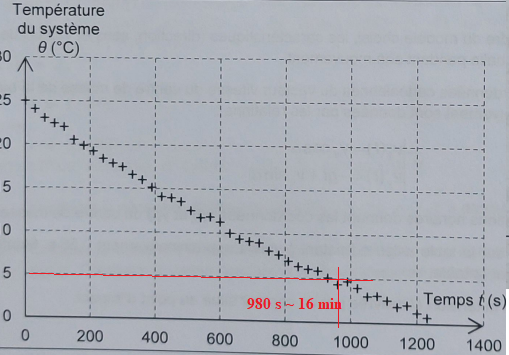5. Dans l'hypothèse d'un flux thermique constant F au cours du refroidissement, calculer sa valeur. F = Q / Dt = -3,0 104 / 980 ~ -31 J s-1 ou watts. L'expérience montre que le flux évolue au cours du refroidissement. 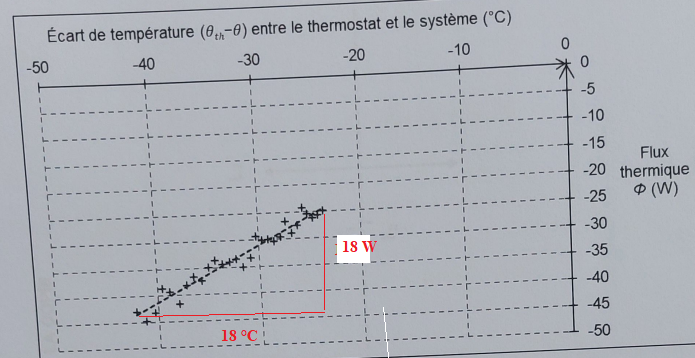La loi de Newton modélise ce flux thermique. F = hS (qth-q) h : coefficient d'échange thermique surfacique ; S =3,1 10-2 m2 surface d'échange ; qth = -18°C température de l'air à l'intérieur du congelateur. 6. Interpréter la courbe ci-dessus ; déterminer h, commenter. Le flux thermique est proportionnel à l'écart de température. F = 18 / 18 Dq =Dq. 1 = hS ; h =1 / (3,1 10-2) ~32 W m-2 K-1. Cette valeur appartient à l'intervalle 5 ; 50 W K-1 m-2, (interface paroi solide -air) Evolution temporelle de la température : q(t) = (qi -qth) exp(-hS t / C) +qth. 7. Commenter l'évolution temporelle de q(t) . Définir le temps caractéristique t et le calculer. La température suit un exponentielle décroissante.  t = C /( hS), il caractérise la rapidité de l'évolution de la température du système. t = 1,50 103 / 1 =1,5 103 s. 8. En s'appuyant sur les données expérimentales de le figure 1, par exemple en exploitant la tangente à l'origine, évaluer le temps caractéristique et commenter. 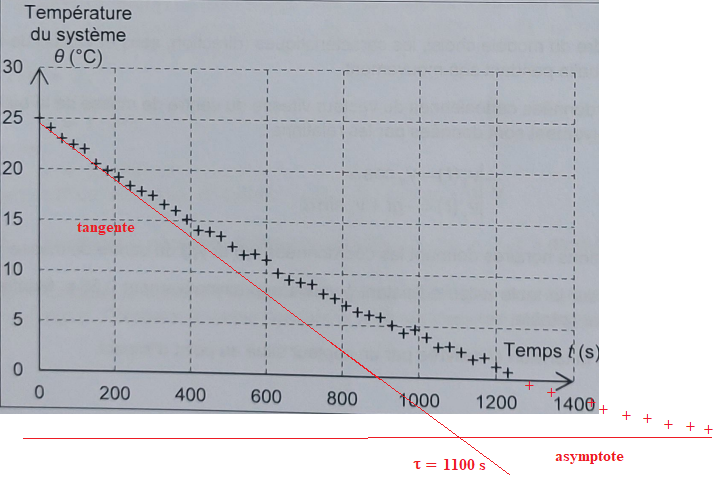Ces deux valeurs sont différentes. Le refroidissement de la canette n'obéit pas à la loi de Newton.

menu