Mathématiques,
concours TSPEI 2020.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Premier problème.
A. Etude d'une équation du troisième degré.
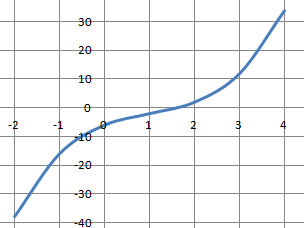
On considère la fonction f définie sur R par f(x) = x3-3x2+6x-6.
1. Calculer f(0), f(1) et f(2).
f(0) = -6.
f(1) = 1-3+6-6 = -2.
f(2) =8-12+12-6=2.
2. Déterminer la limite de f en +oo et -oo.
Quand x tend vers -oo, x3 tend vers -oo ; il en est de même de f(x).
Quand x tend vers +oo, x3 tend vers +oo ; il en est de même de f(x).
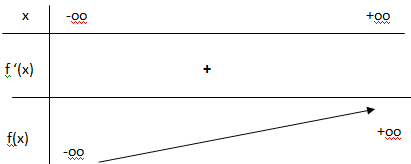
3. Etudier les variations de f et donner le tableau de variation.
f '(x) = 3x2-6x+6.
Solutions de 3x2-6x+6 =0.
Discriminant D =(-6)2-4 *6*3= -36. Aucune racine réelle.
f '(x) >0 et f(x) est strictement croissante.
On considère l'équation (E) : x3-3x2+6x-6 =0.
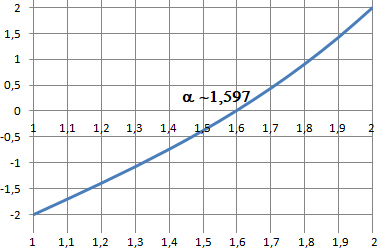
4. Motrer que (E) admet une unique racine réelle, notée a située dans l'intervalle [1 ; 2].
f(x) est continue car dérivable ; f(x) est strictement croissante ; a appartient à l'intervalle des images.
D'après le théorème des valeurs intermédiaires, (E) admet une solution unique sur ,[1 ; 2 ].
5. Montrer que (E) est équivalente à l'équation : 3(x2+2) / (x2+6) = x.
3(x2+2) = 3x2+6.
(x2+6) x = x3+6x.
3x2+6 = x3+6x soit x3-3x2+6x-6 =0.
B. Construction d'une suite.
Soit I l'intervalle [1 ; 2 ].
On considère la fonction g définie sur I par g(x) = 3(x2+2) / (x2+6).
1. Calculer g(1) et g(2). Etudier les variations de g sur I.
g(1) = 9 / 7 ; g(2) =18 / 10 = 9 / 5.
Calcul de g '(x) en posant u =3(x2+2) et v = x2+6.
u' = 6x ; v' = 2x.
g'(x)=(u'v-v'u) / v2 = [6x(x2+6) -6x(x2+2)] / (x2+6)2=24x /(x2+6)2.
g'(x) > 0, g(x) est strictement croissante sur I.
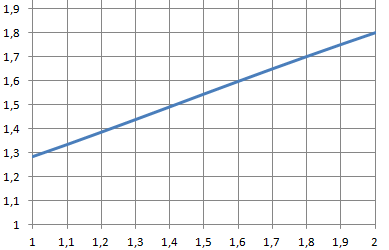
2. Montrer que, pour tout x de I, g(x) appartient à I.
g(x) est strictement croissante sur I.
g(1) = 9 / 7 ; g(2) =1,8. 9 / 7< g(x) < 9 / 5.
1 < g(x) < 2.
3. Démontrer que, pour tout x de I, |g '(x)| < 3*2½ / 8.
g"(x) = -24(4x)(x2+6) / (x2+6)4.
g"(x) < 0 sur I ; g'(x) est strictement décroissante.
g'(1) =24 / 49 ~0,4898 ; g'(2) =0,24. 3*2½ / 8 ~0,53. |g '(x)| < 3*2½ / 8.
4. En déduire que, pour tout x de I, |g(x)-a| < 3*2½ / 8 |x-a|.
g(a) = a ; g'(x) =[g(x)-g(a)] / |x-a| < 3*2½ / 8.
5. On définit la suite (un) par : u0 = 1 et pour tout n > 0, un+1 = g(un).
Calculer u1.
u1 = g(u0) = g(1)= 9 / 7.
6. Démontrer que |un-a| < (3*2½ / 8)n.
Démonstration par récurrence :
Initialisation : |u0-a| = |1-a|< 1. la propriété est vraie au rang 1.
Hérédité : la propriété est supposée vraie au rang n.
|un-a| < (3*2½ / 8)n.
|un+1-a| = |g(un)-a| < 3*2½ / 8 |un-a|.
|un-a| < (3*2½ / 8)n.
|un+1-a|< (3*2½ / 8)n+1. La propriété est vraie au rang n+1.
Conclusion : la propriété est vraie au rang 0 et héréditaire, elle est donc vraie pour tout entier n >0.
|
...
|
....
|
Second problème.
Une association souhaite mener une étude sur la répartition des âges de ses 500 adhérents.
classe d'âge ( ans)
|
]20 ; 30]
|
]30 ; 40] |
]40 ; 50] |
]50 ; 60] |
]60 ; 80] |
effectif
|
40
|
100
|
200
|
125
|
35
|
1. On prélève une fiche au hasard dans le fichier des adhérents. On note A et B les événements suivants :
A : la fiche est celle d'un personne dont l'âge est inférieur ou égal à 60 ans.
B : la fiche est celle d'un personne dont l'âge est strictement supérieur à 30 ans.
a. Calculer la probabilité de chacun des événements A, B, A n B. Comment interpréter ce dernier résultat ?
P(A) =(500-35) / 500 =0,93.
P(B) = (500-40) / 500 =0,92.
P(A n B) =(500-40-35) / 500 =0,85.
425 personnes ont un âge compris entre ]30 ; 60].
b. Calculer la probabilité de B sachant que A est réalisé.
PA(B) = P(A n B) / P(A) =0,85 / 0,93 ~0,91.
2. On prélève au
hasard et avec remise 40 fiches dans le fichier des adhérents. Soit X
la variable aléatoire qui associe à chaque prélèvement de 40 fiches le
nombre de fiches correspondant à des personnes dont l'âge est
strictement supérieur à 60 ans.
a. Quelle est la loi de probabilité de X ? on donnera ces paramètres.
Loi binomiale : n = 40 ; p = 35 /500 =0,07.
b. Calculer l'espérance mathématique et l'écart-type de X.
Espérance = np = 40 x0,07 = 2,8.
Ecart type : [np(1-p)]½ =(40 x0,07 x0,93)½ =1,6.
c. Calculer la probabilité de l'événement P(X = 3).
La calculatrice donne P(X = 3) ~0,23.
|
|
|
|