Mathématiques,
concours TSPEI 2021.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
Premier exercice.
Partie A.
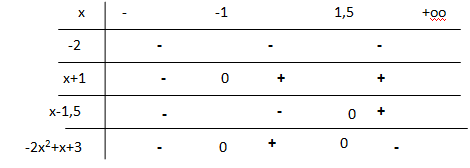
1. Résoudre dans R l'équation -2x2+x+3=0
Discriminant D =1+4*2*3 =25 = 52.
x1 = (-1 +5) / (-4) = -1 ; x2 = (-1 -5) / (-4) = 1,5.
2. Déterminer le signe de -2x2+x+3.
-2x2+x+3=-2(x+1)(x-1,5).
-2x2+x+3 > 0 si x appartient à ]-1 ; 1,5[.
-2x2+x+3 < 0 si x appartient à ]-oo ; -1[ union ]1,5 ; +oo[.
Partie B.
On considère la fonction f définie sur R par f(x) = (2x2+3x)e-x. On note C sa courbe représentative.
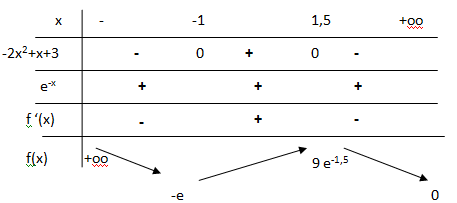
1. Donner les valeurs exactes de f(0), f(-1), f(-1,5) et f(1,5).
f(0) = 0 ; f(-1) = (2-3)e = -e.
f(-1,5) = (4,5-4,5)e1,5 = 0.
f(1,5) = (4,5+4,5)e-1,5 = 9e-1,5.
2.a. Déterminer la limite de f en +oo.
Le terme en exponentielle tend vers zéro ; f(x) tend vers zéro.
2.b. Déterminer la limite de f en +oo.
Le terme en exponentielle tend vers plus l'infini et 2x2 tend vers plus l'infini ; f(x) tend vers plus l'infini.
2.c En déduire l'existence d'une asymptote à la courbe C.
Le droite d'équation y = 0 est asymptote à la courbe C.
3. Calculer la dérivée de f et étudier les variations de f.
On pose u = 2x2+3x et v = e-x.
u' = 4x+3 ; v' = -e-x.
u'v +v'u = (4x+3)e-x-(2x2+3x)e-x=(-2x2+x+3)e-x.
c. Déterminer une équation de la tangente T à la courbe C au point d'abscisse 0.
y = ax +b.
a = f '(0) =3.
Le point de coordonnées (0 ; f(0)=0) appartient à T : 0 =b ; y = 3x.
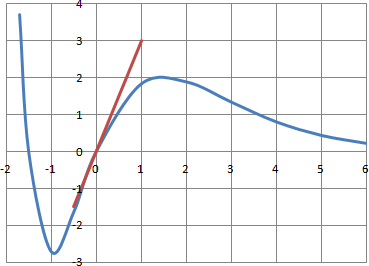
4. Construire C et T.
5. Déterminer selon les valeurs du paramètre réel m, le nombre de solutions de l'équation (2x2+3x)e-x= m.
m < -e : aucune solution.
m = -e : une solution (f(-1).
-e < m < 0 : 2 solutions.
0 < m < f(1,5) : 3 solutions.
m = f(1,5) : 2 solutions.
m > f(1,5) : 1 solution.
6. Calculer l'aire comprise entre la courbe C, l'axe des abscisses et les droites d'équations x =-1 et x = 0.
Intégration par parties en posant f ' = e-x et g=2x2+3x ;
f = -e-x ; g' = 4x+3.
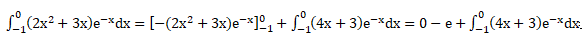
Seconde intégration par parties:
f ' = e-x et g=4x+3 ; f= -e-x ; g' = 4.
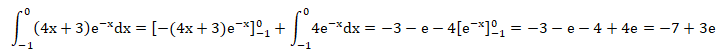
Aire = -e-7+3e =-7+2e ~ -1,56 unités d'aire.
1 unité d'aire = 4 cm2 ; aire ~ -6,25 cm2.
|
...
|
....
|
Second problème.
Une usine fabrique des phares de voitures. Pour fabriquer un phare, un employé a besoin de deux pièces notées P1 et P2. Une seule pièce de type P1 et une seule pièce de type P2 sont nécessaires par phare.
L'usine se fournit auprès de deux sous-traitants S1 et S2.
S1 produit 80 % des pièces de type P1 et 40 % des pièces de type P2.
S2 produit 20 % des pièces de type P1 et 60 % des pièces de type P2.
Un employé réunit toutes les pièces de type P1 et P2
pour fabriquer un certains nombre de phares. Il y a autant de pièces de
chaque type mais elles sont mélangées. Il tire une pièce au hasard.
1. Quelle est la probabilité que la pièce tirées soit de type P1 ?
p = 0,5.
2. Quelle est la probabilité que la pièce tirée soit de type P1 et qu'elle provienne de S1?
p = 0,5 x0,8 = 0,4.
3. Quelle est la probabilité que la pièce tirée vienne de S1 ?
Probabilité que la pièce tirée soit de type P1 et qu'elle provienne de S1 : 0,4.
Probabilité que la pièce tirée soit de type P2 et qu'elle provienne de S1 : 0,5 x0,4 = 0,2.
Total 0,4 +0,2 = 0,6.
L'employé dispose de 200 pièces au total, 100 pièces de type P1 et 100 pièces de type P2. Il tire deux pièces simultanément.
4. Quelle est la probabilité que les deux pièces soient de type P1.
Il y a 200 pièces au total : 100 de type P1
et 100 de type P2
.
Tirer simultanément 2 pièces parmi les 200 c'est à constituer une combinaison de 2 éléments
parmi 200. Il y a (200 2)=200 x199 / 2 =19900
combinaisons possibles.
Parmi toutes ces combinaisons, on s’intéresse à celles étant composées de deux pièces de type P1
.
Il y a (100 2)=100 x99 / 2 =4950
combinaisons possibles composées de deux pièces de type P1
.
Probabilité que ce soit deux pièces P1 : 4950 / 19900 ~ 0,2487.
5. Quelle est la probabilité que, parmi les deux pièces tirées ; l'une soit de type P1 et l'autre de type P2 ?
Tirer une pièce de type P1
parmi 100 c'est constituer une combinaison de 1 élément parmi 100.
Tirer une pièce de type P2
parmi 100 c'est constituer une combinaison de 1 élément parmi 100.
Nombre de combinaisons composées de pièce de type P1
et d’une pièce de type P2
est
:
(100 1x)(100 1) =100 x100 = 10 000.
Probabilité que ce soit une pièce de type P1
et une de type P2
est 10 000 / 19 900 ~0,5025.
6. Quelle est la probabilité que les deux pièces soient fabriquées par le même fournisseur ?
60% des pièces sont fabriquées par S1
soit 0,60 ×200=120
pièces.
Donc 200−120=80 sont fabriquées par S2.
Tirer 2 pièces fabriquées par S1
parmi 120 c'est constituer une combinaison de 2 éléments parmi
120.
(120 2)=120 x119 / 2 =7140 combinaisons possibles.
Tirer 2 pièces fabriquées par S2
parmi 80 c'est constituer une combinaison de 2 éléments parmi
80.
(80 2)=80 x79 / 2 =3160 combinaisons possibles.
Total : 10300
combinaisons possibles composées de 2 pièces fabriquées par le
même fournisseur.
Probabilité que ce soient deux pièces fabriquées par le même fournisseur est 10300 / 19900~0,5176.
|
|
|
|