Fonctions, Mathématiques, bac général La Réunion 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Sujet 1. On considère la fonction f définie sur ]0 ; +∞[ par : f (x) = 3x +1−2x ln(x).  On admet que la fonction f est deux fois dérivable sur ]0 ; +∞[. On note f ′ sa dérivée et f ′′ sa dérivée seconde. On note Cf sa courbe représentative dans un repère du plan. 1. Déterminer la limite de la fonction f en 0 et en +∞. Quand x tend vers zéro : ln(x) tend vers -oo et x ln(x) tend vers zéro. f(x) tend vers 1. Quand x tend vers +oo : f(x) = x ( 3+1/x-2ln(x)). 1 / x tend vers zéro ; ln(x) tend vers +oo ; -2 ln(x) tend vers -oo et f(x) tend vers -oo.  2. a. Démontrer que pour tout réel x strictement positif : f ′ (x) = 1−2ln(x). Dérivée de  x ln(x) : on pose u = x ; v = ln(x) ; u' = 1 ; v' = 1 /x ; u'v+v'u = ln(x) +1. f(x) = 3-2(ln(x)+1) = 1-2ln(x).  b. Étudier le signe de f ′ et dresser le tableau de variation de la fonction f sur l’intervalle ]0 ; +∞[. On fera figurer dans ce tableau les limites ainsi que la valeur exacte de l’extremum. 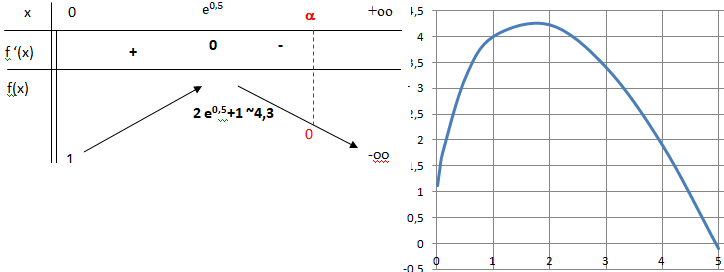3. a. Démontrer que l’équation f (x) = 0 admet une unique solution sur ]0 ; +∞[. On notera a cette solution. Sur ]0 ; e0,5[, f(x) est strictement positive : f(x) = 0 n'a pas de solution. Sur ]e0,5, +oo[ f(x) est continue et strictement décroissante, passant d'une valeur positive à une valeur négative. D'après le corollaire du théorème des valeurs intermédiaires, l'équation f(x) = 0 possède une solution unique sur cet intervalle.  b. En déduire le signe de la fonction f sur ]0 ; +∞[. Sur ]0 ; a[, f(x) est strictement positive ; sur ] a ; +oo[, f(x) est strictement négative.  4. On considère une primitive quelconque de la fonction f sur l’intervalle ]0 ; +∞[. On la note F. Peut-on affirmer que la fonction F est strictement décroissante sur l’intervalle ] e0,5 ; +∞[ ? Justifier. f est la dérivée de F ; f est strictement négative sur ] a ; +∞[  ; donc F est décroissante sur cet intervalle. f est strictement positive sur ] e0,5 ; a[  ; donc F est croissante sur cet intervalle.  5. a. Étudier la convexité de la fonction f sur ]0 ; +∞[. Quelle est la position de la courbe Cf par rapport à ses tangentes ? f ''(x) = -2 /x < 0. La fonction f est concave et la courbe Cf se situe au dessous de ces tangentes.  b. Déterminer une équation de la tangente T à la courbe Cf au point d’abscisse 1. Coefficient directeur de T : f '(1) =1. Le point de coordonnées (1 ; f(1) =4) appartient à T : 4 = 1+b ; b = 3. Equation de T : y = x+3.  c. Déduire des questions 5. a et 5 .b que pour tout réel x strictement positif : ln(x) > 1− 1/ x . Cf étant au dessous de ces tangentes : f(x) < x+3. 3x+1-2x ln(x) < x+3. 2x-2 < 2x ln(x). Diviser chaque terme par 2x : 1-1 /x < ln(x). ... .... Sujet 2. 1. On considère la fonction f définie sur R par f (x) = 2xe x . Le nombre de solutions sur R de l’équation f (x) = − 0,73 est égal à :  a. 0;  b. 1 vrai ; c. 2 ;  d. une infinité. On calcule f '(x) en posant u = 2x ; v = ex ; u' = 2 ; v' = ex. u'v +v'u =2ex+2xex =2ex(1+x). f '(x) < 0 si x < -1 ; f(x) est décroissante sur ]-oo ; -1[ En moins l'infini f(x) tend vers zéro ; f(-1) = -2 e-1~ -0,74. -0,73 est hors de cet intervalle.  Sur ]-1 ; +oo[ ;f '(x) > 0 ;  f(x) est croissante sur ]-1 ; +oo[ . f(x) tend vers plus l'infini si x tend vers plus l'infini. Cette fonction est continue car dérivable et strictement croissante : elle prend une seule fois la valeur -0,73. 2. On considère la fonction g définie sur R par : g(x) = (x +1 ) /e x . La limite de la fonction g en moins l'infini est égale à :  a. −oo vrai ;  b. +oo ;  c. 0 ;  d. elle n’existe pas. En moins l'infini : ex tend vers zéro ; 1 /ex tend vers plus l'infini ;  x+1 tend vers moins l'infini ; Par produit des limites,  f(x) tend vers moins l'infini. 3. On considère la fonction h définie sur R par : h(x) = (4x −16)e2x . On note Ch la courbe représentative de h dans un repère orthogonal. On peut affirmer que : a. h est convexe sur R.  b. Ch possède un point d’inflexion en x = 3. Vrai.  c. h est concave sur R. d. Ch possède un point d’inflexion en x = 3,5. On calcule h'(x) en posant : u = 4x-16 ; v = e2x ; u' =4 ; v' = 2e2x ; u'v+v'u = 4e2x+(8x-32)e2x = e2x(8x-28). On calcule h''(x) en posant : u = 8x-28 ; v = e2x ; u' =8 ; v' = 2e2x ; u'v+v'u = 8e2x+2(8x-28)e2x = e2x(16x-48)= 16 e2x(x-3). Le signe de h ''(x) est celui de x-3. La dérivée seconde s'annule en x =3 et change de signe. Le point de coordonnées (3 ; h(3)) =-4e6) est le seul point d'inflexion. 4. On considère la fonction k définie sur l’intervalle ]0 ; +oo[ par : k(x) = 3ln(x)− x. On note C la courbe représentative de la fonction k dans un repère orthonormé. On note T la tangente à la courbe C au point d’abscisse x = e. Une équation de T est :  a. y = (3−e)x ; b. y = ( 3−e) / e  x  ; vrai. c. y = ( 3 / e −1 ) x +1  ; d. y = (e−1)x +1. k'(x)=3 / x-1 ; Coeficient directeur de T : 3 /e -1. Le point de coordonnées (e ; k(e)) = 3-e appartient à T. Equation de T : y = (3 /e -1) x+b. 3-e = (3/e-1) e +b ; 3-e = 3-e+b ; b=0 y = (3 /e -1) x = (3-e) / e x. 5. On considère l’équation [ln(x)]2 +10ln(x)+21 = 0, avec x appartenant à ]0 ; +∞[. Le nombre de solutions de cette équation est égal à :  a. 0 ;  b. 1;  c. 2 vrai ;  d. une infinité. On pose X = ln(x) ; X2+10X+21=0 Discriminant D =102-4*21=16 = 42. X1 =(-10 +4) / 2 = -3 ; X2 =(-10 -4) / 2 = -7 ; x1 = e-3 ; x2 = e-7.

menu