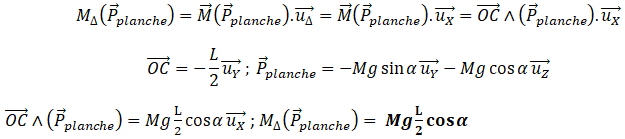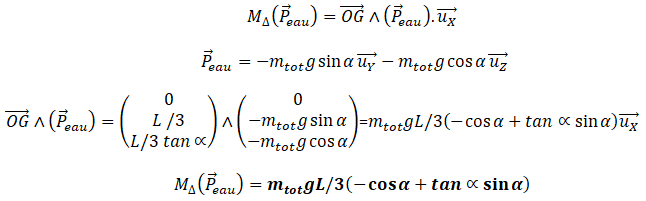Oscillateurs de relaxation, concours G2E ( Géologie, Eau, Environnement )2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Les oscillateurs de relaxation sont des systèmes qui oscillent indéfiniment et périodiquement entre deux états d’énergie différente. Leur évolution n’est pas sinusoïdale et nécessite une source extérieure d’énergie. Dans ce problème nous étudions des exemples d’oscillateurs de relaxation dans des contextes physiques très différents. Les exercices proposés sont complètement indépendants. 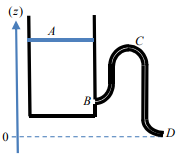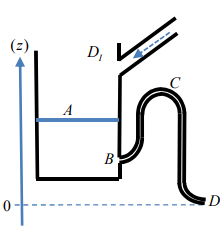1. La bascule à eau : un oscillateur de relaxation mécanique.  Le système ci-dessous constitue un premier exemple d’oscillateur de relaxation. Un robinet alimente régulièrement un récipient posé sur le côté droit d’une balançoire initialement inclinée à gauche (schéma A). Le poids de l’eau finit par faire basculer la planche (schéma B) et le récipient se déverse sur la droite (schéma C), puis remonte et retrouve sa position initiale A. Dans cet exercice nous allons déterminer à quelle condition un tel basculement est possible.  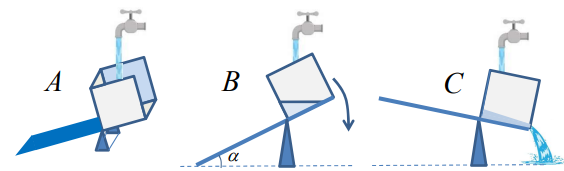La bascule est constituée d’une planche rectangulaire homogène de masse M , de largeur L et de longueur 3L . Cette planche est initialement inclinée d’un angle a par rapport à l’horizontale. Elle peut pivoter sans frottement autour d’un axe horizontal D parallèle à son petit côté et passant aux 2/3 de sa longueur (schéma ci-dessous). Le récipient a la forme d’un cube de côté L (ouvert sur le haut et sur le côté droit). Sa masse est négligeable. 1.1 Exprimer le moment du poids de la planche par rapport à l’axe D en fonction de M, g, L et a , dans la position A. On conviendra que l’axe D est orienté vers le lecteur, c'est-à-dire dans la direction ( X ) du schéma ci-dessous. 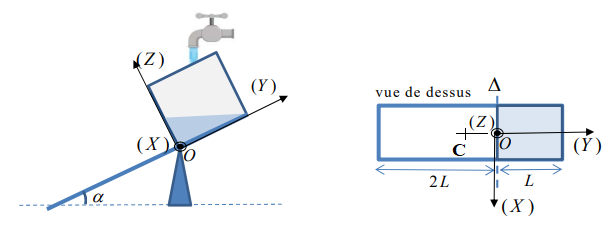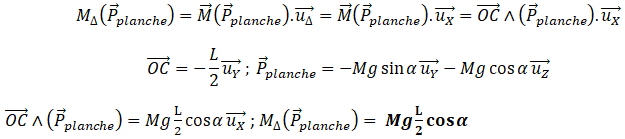Cette valeur étant positive, le poids fait tourner la planche dans le sens trigonométrique direct. On suppose pour l’instant que l’eau est montée jusqu’au bord droit du cube sans que la planche ne pivote, comme indiqué sur le schéma. 1.2. Exprimer la masse mtot de l’eau contenue dans le récipient en fonction de sa masse volumique r , de L et de a . Aire de base =½L2 tan a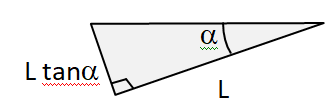 Volume d'eau V = ½L3 tan a. Masse d'eau: mtot = ½ r L3 tan a. 1.3. Soit G le centre de masse de l’eau contenue dans le récipient à cet instant. Définir G. On ne demande pas de calculer explicitement ses coordonnées. On admet que dans le repère orthonormé direct lié à la planche de la balançoire (voir schéma ci-dessus), les coordonnées de G valent XG=0, YG = L/3 ; ZG = L / 3 tan a. Le centre de masse d'un corps est un point imaginaire de référence situé à la position moyenne de la masse du corps.  1.4. Exprimer en fonction de mtot , g et a les coordonnées dans ce même repère  du vecteur Peau  poids de l’eau dans le récipient. En déduire  le moment du poids de l’eau par rapport à l’axe de rotation 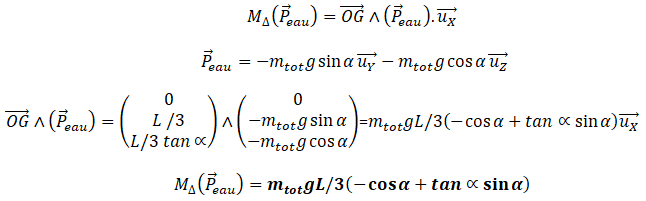 1.5. En déduire qu’une première condition nécessaire pour le basculement de la planche est que a < 45° . En donner une interprétation géométrique simple. Cette condition étant remplie, quelle est la valeur maximale Mmax de la masse M de la planche qui autorise un basculement au cours du remplissage du réservoir ? Calculer Mmax pour : a= 30° , r=1,0 103  kg m-3 et L =50 cm . Le moment du poids de l'eau doit être négatif pour provoquer le basculement. -cos a + tan a sin a < 0 ; cos a > sin2 a / cos a ;  cos2 a > sin2 a  ; a < 45° . La valeur absolue moment du poids de l'eau doit de plus être supérieur au moment de la planche. mtot g L / 3 ( cos a -tan a sin a) > Mg L / 2 cos a ; mtot  / 3 ( 1 -tan2 a ) > M / 2 ; ½ r L3 tan a / 3 (1 -tan2 a ) > M / 2 ; r L3 tan a / 3 ( 1 -tan2 a ) > M ; 1,0 103 x0,53 tan 30 / 3(1 -tan230) > M ; M < 16 kg. 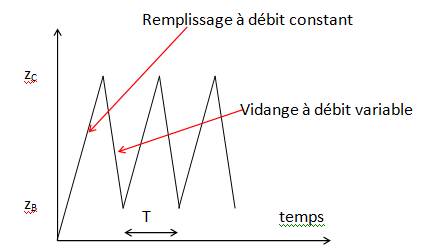2. Le geyser : un oscillateur de relaxation en thermodynamique.  Un geyser est constitué d’une cavité souterraine de volume V située approximativement à une profondeur h sous la surface terrestre, à laquelle il est relié par un conduit. Le tout est rempli d’eau liquide, de masse volumique r= 1,00 . kg / L supposée ici indépendante de la température et de la pression. La température de surface vaut T0= 300 K et le gradient géothermique vaut g=1,00° . C m-1  (i.e. la température de la roche et de l’eau du geyser augmente de 1°C lorsqu’on descend de 1 mètre). La pression atmosphérique vaut P0=1,013 105 Pa. On admet que la vapeur d’eau, même saturante, se comporte ici comme un gaz parfait. La masse molaire de l’eau vaut M=18,0 g / mol. 2.1. Donner l’allure de la courbe de saturation associée à l’équilibre liquide vapeur dans le diagramme (P,V). Placer le point critique C' et les domaines d’existence du liquide, de la vapeur, et du mélange liquide vapeur. Représenter sur ce graphique une isotherme à une température T inférieure à la température critique. Qu’appelle-t-on pression de vapeur saturante à la température T ? Que vaut la pression de vapeur saturante de l’eau à T =100 °C ? 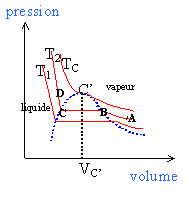La courbe en pointillés est appelée courbe de saturation, lle se compose de 2 parties: - courbe d'ébullition pour V< VC'. -courbe de rosée pour V>VC'. Au point critique C' les deux branches se raccordent. La pression de vapeur saturante est la pression à laquelle la phase gazeuse  d'une substance est en équilibre avec sa phase liquide à une température donnée. La pression de vapeur saturante de l’eau à T =100 °C vaut 1,013 105 Pa.  2.2. Dans la suite on verra que h est de l’ordre de 200 mètres. Déterminer la pression correspondante P(h) dans la cavité, l’eau dans le geyser étant liquide et immobile. Si de la vapeur se forme dans la cavité, quel est son volume molaire vG ? Comparer le volume molaire vL de l’eau liquide à celui du gaz vG. Une mole d'eau ( 18 g) occupe un volume molaire vL = 18 mL. P(h) = Patm + rgh. vG = RT / P(h) avec T = 300 + h. vG = 8,31(300+h)/ (Patm + rgh). Si h = 100 m : vG =8,31 x 400 /(1,013 105 +1000 x9,81 x100)=3,07 10-3 m3 >> vL. Si h = 10 m : vG =8,31 x 310 /(1,013 105 +1000 x9,81 x10)=1,3 10-2 m3 >> vL.  On admet que l’enthalpie de vaporisation (ou chaleur latente) L obéit à l’équation de Clapeyron : L=T(vG-vL) dPv sat /dT . Dans cette expression, Pv sat , est la pression de vapeur saturante, qui ne dépend que de la température T . Dans la suite on néglige vL devant vG , et on considère L comme une constante.  2.3. Montrer qu’avec les approximations faites, l’expression , Pv sat(T) =A exp(-L/ (RT) est solution de l’équation de Clapeyron, où A est une constante. L=T vG  dPv sat /dT  ; dPv sat /dT =L / (T vG) ;  vG = RT / Pv sat pour une mole. dPv sat /dT =L  Pv sat/ (RT2 ) ; dPv sat / Pv sat= L / R dT / T2; Intégrer : ln(Pv sat) = -L/(RT)+ Cste ; Pv sat =A exp(-L/ (RT). On rappelle que la température d’ébullition de l’eau vaut , 373 K à la pression atmosphérique P0 . On mesure L= 40,0 kJ mol-1 . 2.4. En déduire la valeur numérique de la constante A avec trois chiffres significatifs (vérifier que A est proche de 4 1010 Pa). A = P0 exp(L/ (RT) = 1,013 105 exp(40,0 103 /(8,314 x373)= 4,05 1010 Pa. Sur le graphe ci-dessous on a représenté la pression de vapeur saturante et la pression hydrostatique (en Pascal) en fonction de la profondeur (en mètres). Dans le cas d’un geyser, l’ébullition se produit d’abord dans la cavité (ce qui explique la grande quantité de vapeur formée). On note H la profondeur à laquelle la pression P de l’eau dans la cavité coïncide avec la pression de vapeur saturante Pv sat , à la température imposée par le gradient géothermique. 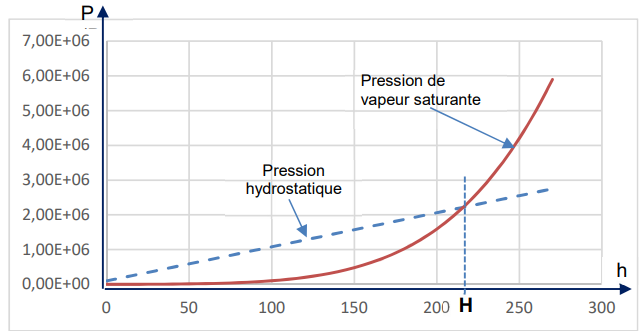 2.5. Comparer la profondeur h de la cavité du Geyser à H . Justifier. Lorsque la pression de l'eau dans la cavité est égale à la pression de vapeur saturante, l'eau se vaporise : h = H.  Pour une profondeur comprise entre 0 et H , le potentiel chimique µV de l’eau vapeur est-il inférieur ou supérieur à celui µL de l’eau liquide ? Ecrire l’équation permettant en principe de calculer H . La solution numérique de cette équation est H = 217 m. Pour une profondeur comprise entre 0 et H ,l'eau est sous forme liquide : µL > µV. A l'état d'équilibre, l'égalité des potentiels chimiques conduit à : µL(T) = µG(T) + RT ln( Psat / P°). Pour le liquide : P(h) = Patm + rgh. Pour la vapeur : Pv sat =A exp(-L/ (RT). Patm + rgh = A exp(-L/ (RT). Dans la suite on supposera que la profondeur h de la cavité vaut exactement H . Dès le début de l’ébullition dans la cavité, les bulles remontent dans le conduit et expulsent rapidement l’eau qui s’y trouvait. Le conduit ne contient alors quasiment plus que de la vapeur d’eau et de l’air, et la pression dans la cavité passe subitement à la pression atmosphérique, alors que la température T de l’eau y est encore égale à celle de la roche environnante. Cette situation éloignée de l’équilibre conduit à une intensification soudaine de l’ébullition de toute l’eau de la cavité. On note c =4,18 J K-1 g-1 la capacité thermique massique de l’eau liquide, supposée indépendante de la température, m la masse d’eau contenue dans la cavité, et mV la masse de vapeur produite à chaque éruption du geyser. On mesure mV =44,0 103 kg. On néglige tout transfert de chaleur avec la roche pendant l’éruption. Pour déterminer m, on admet que l’on peut appliquer la relation approximative suivante : mcDT +nV L=0  où nV est la quantité de matière de vapeur formée et , DT = Téb atm-Tgéo(h)  représente l’écart de température de l’eau liquide entre sa valeur initiale dans la cavité et la température d’ébullition à la pression atmosphérique.  2.6. Proposer une interprétation simple de cette relation. En déduire la masse m et le volume V de la cavité. L'énergie libérée par l'eau liquide sert uniquement à vaporiser le liquide : le système, l'eau liquide, est adiabatique. m = -nV L/ (cDT) ; DT = Téb atm-Tgéo(H) = 373 -(373+217)= -217 K. L=4,00 104 J / mol ; nV = 44,0 103 / M(H2O) = 2,44 106 mol. m = 2,44 106 x4,00 104 /(4,18 103 x217)=1,08 105 kg. Volume de la cavité : m / reau =1,08 105 / 1000 = 108 m3.  2.7. On assimile la cavité à une sphère et on suppose qu’après éruption du geyser, la cavité se remplit rapidement avec de l’eau froide à la température Tf=300 K qui se mélange à l’eau chaude restante. Quelle est la température de l’eau dans la cavité juste après le remplissage ? Qu’est-ce qui détermine essentiellement la période d’éruption ? Masse d'eau chaude restante à la température de 517 K : m-mV =1,08 105-4,40 104=6,38 104 kg. Volume de cette eau : 6,38 104 / 1000 = 63,8 m3. Volume d'eau froide à 300 K : 108-63,8 =44,2 m3 ( 4,42 104 kg). Energie cédée par l'eau chaude : 6,38 104  c ( Tfin -517). Energie gagnée par l'eau froide : 4,42 104  c ( Tfin -300). 6,38 104  c ( Tfin -517) +4,42 104  c ( Tfin -300)=0 6,38  ( Tfin -517) +4,42  ( Tfin -300)=0. 10,8 Tfin -3,30 103 -1,326 103 =0 ; Tfin =428 K. La période du cycle d'éruption est déterminée par la durée d'élévation de la température de l'eau froide de 300 K à 517 K. ... .... Un oscillateur de relaxation électronique. Les portes logiques P1 et P2 utilisées dans le montage ci-dessous sont des composants actifs, qui ont leur propre alimentation. Ce sont des inverseurs : leur caractéristique est indiquée sur le schéma ci-dessous à droite : pour une tension d’entrée UE inférieure à la tension de basculement VB , la tension de sortie US vaut E (avec E >VB). Lorsque l’entrée UE passe au-dessus de VB , la sortie US passe de E à 0. L’impédance d’entrée des portes est considérée comme infinie : les courants d’entrée (à gauche des portes) sont nuls. Par contre leur courant de sortie est a priori quelconque. Nous allons déterminer la période des oscillations du potentiel des points du circuit. On suppose que le système se trouve initialement dans l’état suivant : US2=UE1=E,  US1=0, UC=0, (le condensateur de capacité C et de tension UC est déchargé). 3.1. Justifier sans calcul que la tension UE2 va varier. Va-t-elle diminuer ou augmenter ? US1=Uc =0, condensateur déchargé. UE2 = US1 + Uc = 0. UE2 va croïtre.  Cette phase s’achève lorsque UE2 atteint VB et nous choisirons cet instant comme origine des temps. A t =0 (c’est-à-dire juste avant le basculement), on a donc US2=UE1=E, US1=0, et UE2=VB. La porte 2 bascule. 3.2. Que valent ces tensions à l’instant t =0+ , juste après le basculement de la porte 2 ? Justifier. Écrire l’équation différentielle vérifiée par la tension Uc(t) aux bornes du condensateur dans la phase qui suit. En déduire l’expression de Uc(t), en fonction de E, VB, R, C et t , puis celle de UE2 ( t)  pendant cette phase. US2(0+)= 0 = UE1(0+) ; US1(0+)= E ; UE2(0+)=VB ; US1(0+)+UC(0+)=UE2(0+)=VB ; US1+ Uc +UR = US2 ;  E+ Uc +UR = 0. UR =R i(t) = RC dUc/dt ; RC dUc/dt  +Uc= - E. On pose t = RC ; Uc(t) = A exp(-t / t) -E avec A une constante. Uc(0) = A -E=UE2=VB ; A = E + VB. Uc(t) = (E + VB) exp(-t / t) -E. UE2 = Uc(t) + US1 = Uc(t) + E ; UE2 =(E + VB) exp(-t / t). Cette phase s’achève à l’instant TB pour lequel UE2 atteint de nouveau VB. 3.3. Vérifier que TB = RC ln[(VB+E) / VB] . UE2(t) diminue et lorsqu'elle atteint la valeur VB il y a basculement. UE2(TB)= VB=(E + VB) exp(-TB / t). VB /(E + VB) =exp(-TB / t). ln[(E + VB) / VB] =TB / t ; TB = RC ln[(VB+E) / VB]. 3.4. Que vaut la tension UC à t=TB- (juste avant TB ) ? Que valent les tensions US2, UE1, US1, UE2 et UC à t = TB+ (juste après TB ) ? A TB-, la porte n'a pas encore basculé  : US2 = UE1 = 0 ; US1 = E ; UE2 = VB ; UC = UE2 - US1 =VB-E. A TB+, la porte vient de basculer  : US2 = UE1 = E ; US1 = 0 ;  UC =VB-E ; UE2 + US1 =VB-E.  3.5. Montrer que dans la phase qui suit, UE2(t) =E+(VB-2E) exp[(t-tB) / (RC)]. Le condensateur se charge durant cette phase. Uc +UR = E ; Uc +RC dUc /dt = E ; dUc /dt + Uc / t = E / t. Solution de l'équation sans second membre : Uc(t) = B exp[-(t-tB) / t] avec B une constante. Solution particulière : Uc = E. Solution de l'équation différentielle : Uc(t) = B exp[-(t-tB) / t] +E. A t = TB+ : Uc = B +E = VB - E ; B = VB -2 E. Uc(t) = (VB -2 E ) exp[-(t-tB) / t] +E= UE2(t).  3.6. Un nouveau basculement se produit à l’instant T=TB+TH. Etablir l’expression de TH et de T en fonction de R, C, E et VB . Justifier que T peut être qualifiée de période des oscillations. Lorsque UE2 = VB, il y a un nouveau basculement. VB = (VB -2 E ) exp[-TH / t] +E. (VB-E) / (VB -2 E )= exp[-TH / t] ln[(VB-2E) / (VB -E )] = TH / t]. TH =RC ln[(VB-2E) / (VB -E )]. T = TB+TH =RC ln[(VB+E) / VB] + RC ln[(VB-2E) / (VB -E )]. T = RC ln[(VB+E)(VB-2E) / ((VB -E )VB)]. T correspond à un cycle de charge et décharge complète du condensateur. 3.7. Calculer T pour : R = 100 kW, C=10 nF, E=10 V, VB=5 V. RC = 105 x10-8=10-3 s ; T =10-3 x ln[ 15 x(-15) / (-5 x5)]=2,2 10-3 s. Le siphon : un oscillateur de relaxation en mécanique des fluides. On considère un réservoir cylindrique d’axe vertical (Oz) orienté vers le haut, dont la base a pour aire S. Ce réservoir est rempli d’eau jusqu’à une certaine altitude h (soit h=zA)  pour un certain point A en surface). La partie basse de ce réservoir est percée d’un trou (point B), au contact d’un siphon (B-C-D), qui est une conduite de forme coudée et de section d’aire constante s très petite devant S. La surface libre de l’eau (en A) et la sortie du siphon (point D) sont en contact avec l’air libre (pression atmosphérique P0 ). D est plus bas que B, qui est lui-même plus bas que A. L’altitude de référence z = 0 est celle du point D, et les points B et C sont à des altitudes constantes zB et zC . Dans les calculs qui suivent nous allons considérer que le siphon est amorcé : il est entièrement rempli d’eau, considérée comme un fluide homogène de masse volumique r et incompressible : le siphon ne contient pas d’air. Dans ces conditions nous allons déterminer le temps de vidange du réservoir. On note g l’intensité de la pesanteur. 4.1. Ecrire le théorème de Bernoulli le long d’une ligne de courant entre un point A à la surface de l’eau et un point D à la sortie du siphon. On suppose que les conditions d’application de ce théorème sont vérifiées. Quelles sont ces conditions ? Pour un fluide parfait, homogène et incompressible, en écoulement permanent dans un référentiel galiléen : ½v2A+gzA +PA / r =½v2D+gzD +PD / r .  4.2. Justifier que la vitesse vA de l’eau en A est très petite devant la vitesse en sortie du siphon vD. Conservation du débit volumique : SvA = svD. S >> s, donc vA << vD. On remarque d’autre part que vA = -h'(t). 4.3. Justifier qu’avec les hypothèses faites, l’altitude h (t) de l’eau dans le réservoir obéit approximativement à l’équation différentielle :  h '+s/S (2g)½ h½ =0. PA = PD = P0 ; v2A+2gzA  = v2D+gzD =v2D ;  vD >> vA, donc 2gh  = v2D =(S / s)2 v2A. vA (S / s) =(2g)½ h½ ; vA -(s / S) (2g)½ h½ =0 ; -h' -(s / S) (2g)½ h½ =0.  h '+s/S (2g)½ h½ =0. 4.4. Résoudre cette équation en supposant qu’à l’instant initial, h(0) = h0 >> zC. En déduire que le niveau d’eau dans le réservoir parvient à l’entrée du siphon (en B) à l’instant t1=(2/g)½S / s[h0½-zB½] . Que se passe-t-il à cet instant ? Séparation des variables : dh / h½ =  -s / S(2g)½ dt. Intégrer entre h0 et h d'une part et entre 0 et t d'autre part : 2 h½ - 2h0½= -s / S(2g)½ t ; h½ - h0½= -s / S(0,5g)½ t ; t1=[h0½-zB½] (2 / g)½S / s. Le siphon se désamorce ensuite.  Afin de modéliser l’écoulement de l’eau dans une grotte, on reprend les calculs précédents en supposant désormais que le réservoir est alimenté en permanence par une arrivée d’eau de débit volumique constant D qui ne perturbe pas l’écoulement de vidange.  4.5. Dans les mêmes conditions que précédemment (le siphon étant rempli d’eau), justifier que la hauteur h de l’eau obéit maintenant à l’équation différentielle h'+s/S (2g)½ h½ = D / S. A chaque seconde, l’altitude h (t) de l’eau dans le réservoir augmente de D / S. h'+s/S (2g)½ h½ = D / S. 4.6. Vérifier que cette équation possède une solution stationnaire, pour une hauteur d’eau hS que l’on exprimera en fonction de , D, s et g . Cette hauteur doit évidemment être supérieure à celle de l’entrée du siphon. A quel débit minimum Dmin cela correspond-il ? En régime stationnaire, h' = 0 : s/S (2g)½ h½ = D / S. s (2g)½ h½ = D ; h½ =D / [ s (2g)½] ; h =D2 / [ s2 (2g)]. Dmin = s (2g)½ hB½ .  4.7. Lorsque le siphon contient de l’air, il ne fonctionne plus ( DS=0 ) : on dit qu’il est désamorcé. Dans ce cas, comment évolue la hauteur d’eau dans le réservoir ? L'eau ne s'écoule plus et la hauteur de l'eau augmente de hB à hC. 4.8. Soit DC le débit volumique sortant par le siphon (amorcé) lorsque h=zC . Exprimer DC en fonction de s, g et zC . Que peut-on dire de l’évolution ultérieure de h si D > DC  v2C+2gzC  = v2D+gzD ; vC << vD et zD = 0 : 2gzC  = v2D. Dc = s vD = s (2gzC)½. Si D > DC , l'eau monte dans le réservoir et va finir par déborder.  Ainsi lorsque D < DC , le siphon évolue entre les deux états : amorcé et désamorcé. On suppose de plus que lorsque le siphon est amorcé, D est négligeable devant le débit de sortie. 4.9. Exprimer dans ces conditions la période des oscillations du niveau d’eau h(t) dans le réservoir. Représenter qualitativement l’allure de ces oscillations. Siphon désamorcé : la durée pour atteindre la hauteur zC est : S(zC-zB) / D. Siphon amorcé : la durée de vidange est S(zC-zB) / Dc. 5. L’oscillateur de relaxation " Stick-slip " un modèle simple en géophysique.  Le coulissement entre deux plaques lithosphériques (faille transformante) peut être modélisé en première approximation par le dispositif suivant : un objet considéré comme ponctuel, de masse m, est posé sur un tapis roulant entraîné à une vitesse v constante (par rapport au sol, considéré comme « fixe »). Cet objet, qui est choisi comme « système », est également relié à un point fixe par l’intermédiaire d’un ressort de raideur k . La position du centre de l’objet est repérée par son abscisse x (axe horizontal). A l’instant t = 0 , le ressort n’est pas tendu (il n’exerce aucune force sur ses extrémités), et l’abscisse de la masse est notée x0 (c’est la longueur à vide du ressort).   5.1. On constate que tant que l’intensité de la force de traction T  exercée par le ressort ne dépasse pas une valeur Tmax , l’objet reste « collé », c’est-à-dire fixe par rapport au tapis. Exprimer alors la loi horaire x (t) durant cette phase. Ecrire une relation simple entre la force de frottement F  exercée par le tapis sur l’objet et la force T  exercée par le ressort. Justifier. En déduire la norme F(t) de la force exercée par le tapis sur l’objet. La vitesse de l'objet par rapport au sol est identique à celle du tapis par rapport au sol. On note v cette vitesse. dx/dt = v ; x(t) = vt + x0. Le système ( objet) dans le référentiel lié au sol, supposé galiléen est telle que T = F= k (L-L0)= k(x(t) -x0)= k v t.. Par contre dès que T atteint la valeur Tmax , l’objet « se décolle » et on considère qu’il glisse sans frottement sur le tapis : F s’annule, et l’objet n’est plus soumis qu’à l’action du ressort. 5.2. A quel instant t1 (à exprimer en fonction de Tmax k, et v ) l’objet décolle-t-il du tapis ? A quelle équation différentielle obéit la position x (t) de cet objet dans la phase qui suit ? L'objet décolle si T = Tmax : F(t1) = k v t1 = Tmax. t1 = Tmax / (kv). Dans la phase qui suit F = 0 et : md2x/dt2 = -k(x-x0). d2x/dt2 +k / m x=k / mx0.  5.3. Justifier que l’on peut écrire la solution de cette équation différentielle sous la forme x(t)=x0 +A sin [w0(t-t1) +a], où A, w0 et a sont des constantes. Exprimer w0 en fonction de k et de m. En tenant compte des conditions initiales, exprimer tan a en fonction de w0 et t1 , et A en fonction de v1t1, et w0. dx(t) /dt=dx0 /dt +Aw0 cos [w0(t-t1) +a]= 0+Aw0 cos [w0(t-t1) +a]. d2x/dt2 = - A w02 sin [w0(t-t1) +a]. Repport dans l'équation différentielle : - A w02 sin [w0(t-t1) +a]+ kx0 / m+ kA / m sin [w0(t-t1) +a] =k /m x0. On pose w02  = k / m. La solution proposée vérifie l'équation différentielle. x(t1) =x0 +A sin a = x0 + v t1. sin a = vt1 / A. v(t) = dx(t) /dt=Aw0 cos [w0(t-t1) +a]. v(t1)=Aw0 cos(a) = v par continuité. cos(a) = v / (Aw0). tan a = w0t1. sin2 a =( v t1 / A)2 ; .cos2 a = [v / (Aw0)]2. sin2 a +cos2 a =1 =v2 / A2[ t12+1/w02]. A = v[ t12+1/w02]½. 5.4. Lorsque la vitesse de la masse par rapport au tapis s’annule à nouveau, la force de frottement F réapparaît. A quel instant t2 cela se produit-il ? (exprimer t2 en fonction de t1 ,a et  w0 ). Vérifier qu’à cet instant, la longueur du ressort vaut x(t2)=x0-Asin a. Continuité de v(t) : v(t2) =Aw0 cos [w0(t2-t1) +a]= v. cos [w0(t2-t1) +a]= v / (Aw0)= cos(a). Solution : w0(t2-t1) +a= - a+2p. t2-t1= 2 / w0[p -arctg(a)] t2=t1+ 2 / w0[p -arctg(a)]. x(t2)=x0 +A sin [w0(t2-t1) +a]. x(t2)=x0 +A sin [ - a+2p] = x0-Asin a.

menu