Mathématiques, suites, équation différentielle, Concours Geipi polytech 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... On considère la suite (un) définie par u0 = 2 et pour tout entier naturel n, un+1 = f(un)) où f est la fonction définie pour tout réel x positif par f(x) = (3x+2) /  (x+4) . On admet que, pour tout entier naturel n, un est supérieur ou égal à 1.  I-1-a- Calculer les valeurs exactes de u1 et u2 . Donner le résultat sous la forme d’une fraction irréductible. u1=(3u0+2) / (u0+4)=8 / 6 = 4 / 3. u2=(3u1+2) / (u1+4)=6 / (16/3)=18 / 16= 9 / 8.  I-1-b- Le graphique ci-dessous donne la courbe représentative dans un repère orthonormé de la fonction f. A partir de ce graphique, que peut-on conjecturer concernant les variations et la convergence de la suite (un) ? Préciser la limite éventuelle. 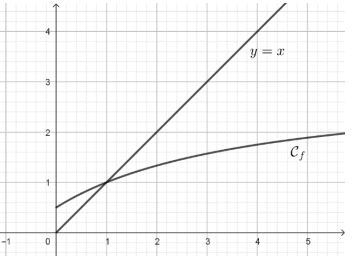La suite est d"croissante et converge vers 1. On se propose d’étudier la suite (un) en utilisant deux méthodes différentes. Méthode 1.  I-2-a- Montrer que, pour tout entier naturel n, un+1 − un = (1−un)(un+2) / (un+4 ) . 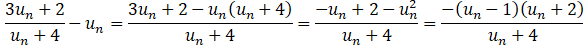I-2-b- En déduire le sens de variation de la suite (un). Justifier la réponse. un > 1 ; un+2 > 0 ; un+4 > 0 ; 1-un < 0 ; un+1 < un : la suite est décroissante.  I-3- Démontrer que la suite (un) est convergente. On note l sa limite. La suite est décroissante et minorée par 1 : donc elle converge. I-4- Déterminer la valeur de l. Justifier la réponse. Quand n tend vers +oo : un =un+1 = l. (3l+2) /  (l+4) =l . 3l+2 =l2+4l ; l2+l -2 =0. Discriminant : (-1)2+4*2 = 9 = 32. La solution positive est retenue :(-1 +3) / 2 = 1.  Méthode 2 On considère la suite (vn) définie pour tout entier naturel n, par : vn = (un−1) /( un+2).  I-5- Calculer v0. v0=(u0−1) /( u0+2) = (2-1) /(2+2)=1 /4 =0,25. I-6-a Déterminer la constante k dans ]0 ; 1[ telle que vn+1 = k × vn pour tout entier naturel n. Justifier la réponse. Que peut-on en déduire sur la nature de la suite (vn) ? vn+1 = (un+1−1) /( un+1+2). 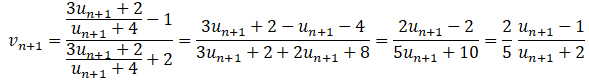La suite (vn) est géométrique de raison k = 0,4 et de premier terme v0 =0,25.  Pour les questions I-6-b et I-6-c, les réponses peuvent être exprimées en fonction de k ou de sa valeur. I-6-b- En déduire l’expression de vn en fonction de n. vn=0,25 x 0,4n. I-6-c- En déduire la convergence de la suite (vn) et sa limite. Justifier la réponse. vn+1-vn=0,25 (0,4n+1-0,4n)=0,25 x 0,4n(0,4-1) < 0. La suite est décroissante. Quand n tend vers +oo : 0,4 n tend vers zéro ; vn tend vers zéro. La suite (vn) étant décroissante et minorée, elle converge.  I-7-a- Exprimer un en fonction de vn pour tout entier naturel n. vn = (un−1) /( un+2) ; un−1 =unvn+2 vn ; un(1-vn)=1+2 vn ; un=(1+2 vn ) / (1-vn).  I-7-b- En déduire la convergence de la suite (un) et sa limite. Justifier la réponse. Quand n tend vers +oo : vn tend vers zéro et un converge vers 1. ... .... Dans cet exercice, K et a sont des constantes réelles strictement positives On considère l’équation différentielle (E1) : z’(t) + z(t) = 1 / K , où z est une fonction définie et dérivable sur [0 ; +∞[ .  II-1- Donner la solution générale de (E1) sur l’intervalle [0 ; +∞[. Solution générale de z’(t) + z(t) =0 : z(t) = A e-t avec A une constante réelle. Solution particulière de (E1) : z =1 / K. Solution générale de (E1) : z(t) = A e-t +1/K. On considère la fonction f définie pour tout réel t positif par : f(t) = 10 / (1+ae-t).  II-2- Compléter le tableau des variations de f sur l’intervalle [0 ; +∞[. Préciser la valeur de f en 0 ainsi que la limite de f en +oo. f '(t)=10 a e-t /(1+ae-t)2 > 0.  II-3- Déterminer, en fonction de a, l’ensemble des solutions de l’équation f(t) = 5. 10 =5 (1+ae-t) ; 2 =1+ae-t ; 1 / a =e-t ; t = ln(a). Partie II – Evolution d’une population de marmottes.  Soit y0 un réel strictement positif. On étudie l’évolution d’une population de marmottes, qui compte initialement y0 milliers d’individus. On admet que la taille de la population, exprimée en milliers d’individus, au bout de t années (avec t ≥ 0) est une fonction y dérivable sur [0 ; +∞[, solution de l’équation différentielle : (E2) ∶ y′ (t) = y(t) (1 − y(t) / K ). La constante K s’appelle la capacité d’accueil du milieu, exprimée en milliers d’individus. On admet qu’il existe une unique fonction y solution de (E2) qui vérifie y(0) = y0. On admet que cette fonction est à valeurs strictement positives sur [0 ; +oo[. On pose z(t) = 1 / y(t) pour tout réel t positif. II-4-a- Exprimer z'(t) en fonction de y '(t) et y(t). z'(t) = - y '(t) / y2(t).  II-4-b- On souhaite montrer que z est solution de (E1) si, et seulement si, y est solution de (E2). Compléter : • la Ligne 1 à l’aide d’une expression utilisant z '(t) et z(t) . z est solution de (E1) : z’(t) + z(t) = 1 / K. • la Ligne 2 et la Ligne 3 à l’aide d’une expression utilisant y’(t) et y(t). -y '(t) / y2(t)+ 1/ y(t) = 1 / K. -y '(t) +y(t) = y2(t) / K ; y '(t) =y(t) ( 1-y(t) / K). y(t) solution de E2.  II-5-a- En déduire la solution générale de (E2). y(t) = 1 / z(t) = 1 / [A e-t +1/K]= K / (AKe-t +1).  II-5-b- On admet que l’unique solution y de (E2) vérifiant y(0) = y0 s’écrit sous la forme y(t) = K/( 1+ a e-t). Exprimer a en fonction de y0 et de K. On identifie a = AK. y0 =K / (1+AK) ; K = y0(1+AK)  K-y0 =y0 AK ; A = (K-y0) / (Ky0). a = (K-y0) / y0. Dans un certain vallon de capacité d’accueil  K = 10, les marmottes ont disparu. Les scientifiques souhaitent réintroduire y0 milliers de marmottes, avec 0 < y0 < 10. Dans la suite de l’exercice, on prendra K = 10.  II-6- Justifier que la valeur de a obtenue à la question II-5-b- est bien strictement positive. a = 10 / y0-1 ; 10 / y0 > 1 ; a >0.  II-7-a- En utilisant le résultat de la question II-3-, donner la valeur de a telle que y(5) = 5. t =5= ln(a) ; a =e5.  II-7-b- En déduire la valeur exacte de y0 telle que y(5) = 5. Justifier la réponse. e5 = K /y0 -1 = 10 /y0-1 ; e5 +1 =10 /y0 ; y0  = 10 /(e5 +1).  II-7-c- La calculatrice donne 0,0669285092 comme résultat au calcul de la valeur de y0 de la question précédente. Quel est le nombre minimal de marmottes à réintroduire pour qu’au moins 5 milliers de marmottes soient présentes au bout de 5 années après leur réintroduction ? Il faut introduire 67 marmottes.

menu