d'après concours kiné ADERF 2004

Une onde mécanique progressive périodique se propage le long d'une échelle de perroquet (ou ondoscope). On constate que la distance minimale séparant deux barreaux oscillant en opposition de phase est de 25cm. La célérité de cette onde est de 1,0 m/s. Quelle est la fréquence de cette onde ?
------> aide
la distance minimale séparant deux barreaux en opposition de phase est ½ longueur
d'onde.
fréquence (Hz) =célérité (m/s) / longueur d'onde(m)
1. 0,020 Hz
2. 0,25 Hz
3. 2,0 Hz
4. 20 Hz
5. 0,25 kHz
Un haut parleur émet une onde sonore de fréquence f = 1,0 kHz. Cette onde se propage dans l'air à la célérité c = 340 m/s . Le haut-parleur est situé face à un mur, à la distance L = 80 m du mur. Un auditeur A, situé entre le haut parleur et le mur entendra simultanément le son émis par le haut parleur et le son réfléchi par le mur si l'intervalle de temps entre les arrivées des deux sons est inférieur à 0,10s.
---> aide:
l'onde incidente atteint l'auditeur à la date t1 =(L-x)/c
l'onde incidente atteint le mur et se réfléchi à la date t =L/c
l'onde réfléchie atteint l'auditeur à la date t2 =t+x/c=( L+x)/c
et t2-t1 inférieure ou égale à 0,1s
t2-t1 = 2x/c

Soit x, la distance entre l'auditeur et le mur. A quelle condition, l'auditeur entendra-t-il les deux sons simultanément ?
1. inférieure à 17 m
2. inférieure à 25 m
3. inférieure à 34 m
4. inférieure à 68 m
5. inférieure à 80 m
On considère deux ondes lumineuses monochromatiques, l'une rouge de longueur d'onde lambdaR dans le vide , l'autre bleue de longueur d'onde lambdaB dans le vide.

Quelles sont les affirmations exactes concernant la célérité de ces ondes ?
1. dans le vide, ces deux ondes ont la même célérité
2. dans le vide, ces deux ondes se propagent à des célérités différentes
3. dans un milieu transparent, la célérité de chaque onde est inférieure à sa valeur dans le vide
4. dans un milieu transparent, la célérité de chaque onde est supérieure à sa valeur dans le vide
5. dans un milieu transparent dispersif, ces deux ondes se propagent à des célérités différentes
Un laser émettant un faisceau de lumière de longueur d'onde lambda est placé devant une fente fine de largeur a. On observe sur un écran situé à la distance D de la fente une tâche lumineuse centrale de largeur d.
On note k une constante non dimensionnée.

Quelle est l'expression de d ?
1. k (lambda a) / D
2. k (a D) / lambda
3. k ( lambda D) / a
4. k (lambda D²) / a
5. k lambda a D
Quelle(s) réaction(s) nucléaire(s) est (sont) une fusion ?
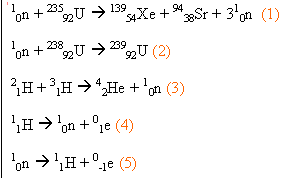
1. (1)
2. (2)
3. (3)
4. (4)
5. (5)
Un échantillon de roche contient 1,0 mg d'un radioélément. A l'instant t = 0, cet échantillon produit 2,4.10^5 désintégrations alpha par minute.
A quelle date, exprimée en fonction de la demi-vie t1/2 du radioélément, l'activité de cet échantillon sera égale à 2,4.10^3 Bq ?
----> aide :
à chaque période ou demi vie l'activité est divisée par 2.
à t½, l'activité est divisée par 2
à 2 t½, elle est divisée par 4
à 3 t½ A est divisée par 8
à 4 t½ A est divisée par 16
à 5 t½ A est divisée par 32......

or ici elle est divisée par 100
1. 0
2. 0,74 t1/2
3. 4,0 t1/2
4. 6,6 t1/2
5. 100 t1/2
La constante de temps d'un ensemble de noyaux radioactifs est 2/ln2 s.

Que peut-on dire de cet échantillon au bout de 4s ?

----> aide :
au bout d'une constante de temps il reste 37 % de noyaux pére initiaux( exponentielle -1)
au bout de deux constante de temps il reste 13% de noyaux père initiaux( exponentielle -2)
4 / constante de temps = 2 ln 2 = 1,4
1. il ne reste plus de noyaux radioactifs
2. il reste 25% du nombre initial de noyaux pères
3. il reste 50% du nombre initial de noyaux pères
4. c) il reste 50% du nombre initial de noyaux pères
  il reste 75% du nombre initial de noyaux pères
5. aucune désintégration n'a encore eu lieu
Un condensateur de capacité C = 900 µF, initialement déchargé est placé en série avec un générateur délivrant un courant sinusoïdal d'amplitude 30mA. La tension maximale aux bornes du condensateur est de 0,50 mV.

Quelle est la fréquence du courant délivré par le générateur ?
----> aide :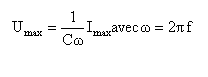
1. 0,10 Hz
2. 10 Hz
3. 1 kHz
4. 10 kHz
5. 10 Mhz
On branche une bobine (inductance L = 100 mH, résistance interne r = 10 ohms) aux bornes d'un générateur de tension (force éléctromotrice E = 10 V, résistance interne R = 10 ohms). A la date t = 0, on ferme le circuit.

A quelle date l'intensité atteint-elle la moitié de sa valeur maximale ?
----> aide
constante de temps : L / (resistance totale du dipole)=0,1 /20= 0,005 s = 5 ms

l'intensité atteint 63% de sa valeur au bout d'une constante de temps
1. 0,13ms
2. 0,7 ms
3. 3,5 ms
4. 7 ms
5. 13 ms
Un dipôle RL est alimenté par le générateur délivrant une intensité de la forme i(t) = 0,05 t, i(t) en ampère et t en seconde (t > 0).

Quelle(s) représentation(s) de la tension u(t) aux bornes du générateur est (sont) possible(s) ?
----> aide :
tension aux bornes d'un générateur de tension u= E-r i(t)
E est positive, fonction affine décroissante à partir de E
1. u(t) = 0
2. une droite passant par l'origine
3. une droite avec une abscisse à l'origine négative
4. une droite à partir d'une certaine date t avant laquelle u(t) = 0
5. une droite avec une abscisse à l'origine positive
Que faut-il faire pour obtenir des oscillations électriques périodiques avec un circuit RLC ?
1. fournir continuellement au circuit l'énergie qu'il perd par par effet joule
2. choisir la valeur de R correspondant au régime apériodique
3. choisir la valeur de R correspondant au régime pseudopériodique
4. choisir la période propre en jouant sur les valeurs de L et C
5. se placer dans le cas où R = 0 ohm
On considère un circuit LC en oscillations libres.

Comment peut-on diviser la période des oscillations par deux ?
----> aide :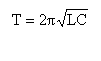
1. doubler C
2. doubler L
3. doubler L et doubler C
4. diviser soit L, soit C par deux
5. diviser L par deux et diviser C par deux
Un objet S de masse m = 1,0 kg est envoyé avec une vitesse initiale vi = racine carrée 6,0 m/s vers le haut selon la ligne de plus grande pente d'un plan incliné d'un angle a = 30° sur l'horizontale. S est soumis, sur la totalité de son trajet, à une force de frottements F (vecteur) opposée à la vitesse et d'intensité constante F = 1,00 N.

Avec quelle vitesse S repasse-t-il par son point de lancement ?
----> aide :
les forces appliquées au solide sont constantes
les points de départ et d'arrivée sont identiques, donc aucune force ne travaille et l'énergie cinétique n'est pas modifiée ( simplement on ira moins haut sur le plan incliné)
1. 1/ racine carrée (6) m/s
2. 0,5 m/s
3. 2 m/s
4. racine carrée (6) m/s
5. 2 racine carré (6) m/s
Un solide en déplacement dans l'air subit une force de frottement fluide de sens opposé au vecteur viresse. Dans le cas d'une vitesse non supersonique, un avion subit une force de frottement F = k.v² .

Dans le système international d'unités, quelle unité est convenable pour k ?
----> aide
force en newton = masse (kg) fois accélération (m/s²)
1. m J.kg-1.s²
2. kg.m/s²
3. kg/ m
4. kg/s²
5. J.kg-1.s²
On étudie la chute verticale d'une bille sphérique métallique (masse volumique ro = 8,0.10^3 kg.m-3) dans un liquide (masse volumique roL = 2,0.10^3 kg.m-3). Le frottement est modélisé par une force F(vecteur) = -6 pi eta r v(vecteur) où eta est une grandeur caractéristique du liquide (eta = 6,0 kg.m-1.s-1), r le rayon de la bille et v (vecteur) la vitesse de la bille. On constate que la vitesse tend rapidement vers une limite de 2,0 cm.s-1 .

Quel est le rayon de la bille ?
----> aide :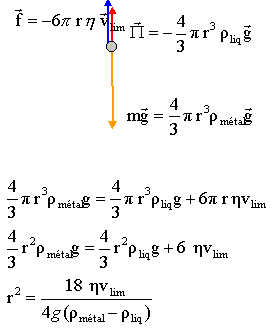
1. racine carrée (6) micromètres
2. 3 micromètres
3. 10 micromètres
4. racine carrée (6) millimètres
5. 3 millimètres
Un pendule simple est constitué d'un solide de masse m = 100 g attaché au bout d'un fil inextensible et sans masse de longueur L = 1,0 m. Les frottements sont négligés. L'autre extrémité du fil est attachée à un point fixe O. Le pendule est écarté d'un angle a = 60° par rapport à la verticale et lancé avec une vitesse vo = 1,0 m.s-1 dirigée vers le bas.

Quelle est la tension du fil lors du passage du pendule par sa position d'équilibre ?
----> aide :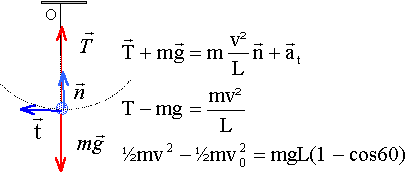
1. 0,1 N
2. 1,1 N
3. 2 N
4. 2,1 N
5. 3,2 N
Un oscillateur élastique horizontal est constitué d'un ressort de raideur k, attaché à un support par une de ses extrémités, et par un solide de masse m lié à l'autre extrémité du ressort.
On écarte le solide de sa position d'équilibre et on laisse l'ensemble osciller à la période T. les frottements sont supposés négligeables.

Quel est l'intervalle de temps minimal entre deux instants où la vitesse et l'accélération sont successivement maximales ?
----> aide :
vitesse maximale au passage à la position d'équilibre (x=0)
l' accélération est maximale lorsque la tension du ressort est maximale ( |x|= amplitude)
1. 0,25 T
2. 0,5 T
3. 0,67 T
4. 0,75 T
5. T
On dispose d'un ressort à spires non jointives, de masse négligeable, et de constante de raideur k = 50 N.m-1. Le travail à fournir pour comprimer de 2 cm ce ressort initialement à sa longueur à vide est de 10 mJ.

Quel est le travail à fournir pour faire passer l'allongement de ce ressort de 4 cm à 10 cm ?
----> aide : Le travail à fournir se retrouve sous forme d'énergie potentielle élastique
W= ½k x² où x est la variation de longueur du ressort
le travail est proportionnel au carré de la variation de longueur
10 m J pour x²= 4 cm²
si l'allongement triple alors le travail est multiplié par 9
1. 30 mJ
2. 90 mJ
3. 150 mJ
4. 210 mJ
5. 270 mJ
Une balle de tennis vient percuter le sol verticalement avec une vitesse de 10 m.s-1 . Au cours du choc, elle perd 36% de son énergie.

Quelle sera sa vitesse immédiatement après le premier rebond ?
----> aide :
l'énergie cinétique diminue de 36% :
avant rebond : 0,5 m v²= 0,5 m*10²= 50 m joule
après rebond : 0,5 mv² = 0,64*50 m
v²= 64
1. 3,6 m/s
2. 6,4 m/s
3. 7 m/s
4. 8 m/s
5. 9,9 m/s
Un point matériel décrit une trajectoire circulaire de rayon r d'un mouvement uniforme.

Quelles sont les affirmations exactes concernant ce mouvement ?
1. le vecteur vitesse est constant
2. la valeur du vecteur vitesse est constante
3. le vecteur accélération est nul
4. la valeur du vecteur accélération est indépendante de r
5. la valeur du vecteur accélération est proportionnelle au carré de la vitesse
On dispose de trois solutions suivantes :
A : solution d'hydroxyde sodium de concentration molaire C1 = 0,01 mol / L
B : solution d'acide éthanoïque de concentration molaire C2 =0,02 mol.L-1 (pKA2 = 4,8)
C : solution d'acide méthanoïque de concentration molaire C3 = 0,01 mol.L-1 (pKA3 = 3,8)
On mélange 100 mL de solution A avec 100 mL de solution B ; on obtient la solution D où se produit la réaction I :
CH3COOH (aq) + HO- (aq) = CH3COO- (aq) + H2O
A cette solution D, on ajoute 100 mL de solution C ; on obtient la solution E où se produit la réaction II.
HCOOH + CH3COO- = HCOO- + CH3COOH

DONNEE : La constante d'équilibre de la réaction d'autoprotolyse de l'eau est Ke = 1,0. 10-14 à 25°C.

Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
1. le pH de la solution A a pour valeur 12
2. la constante d'équilibre de la réaction I a pour valeur 10 exposant 8,2
3. la réaction I évolue dans le sens direct
4. le pH de la solution D a pour valeur 3,8
5. la constante d'équilibre de la réaction II a pour valeur 10
On étudie expérimentalement l'hydrolyse du méthanoate de méthyle. On introduit un mélange équimolaire d'ester de masse m1 = 6,0 g et d'eau de masse m2, puis quelques gouttes d'acide sulfurique, dans un ballon équipé d'un montage à reflux et placé dans un bain-marie. Après 30 minutes de chauffage, le ballon est placé dans de l'eau glacée.
Le titrage de l'acide carboxylique par une solution concentrée d'hydroxyde de sodium montre qu'il s'est formé la masse m3 = 1,5 g d'acide au bout de trente minutes.

DONNEES : Masses molaires en g.mol-1 : H : 1 ; C : 12 ; O : 16.

Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
----> aide :
Qté de matière ester initial 6/ 60 = 0,1 mol
Qté de matière d'acide méthanoïque formé : 1,5 / 46=0,032 mol
à 30 min l' équilibre est atteint
1. la masse d'eau introduite a pour valeur m = 1,8 g
2. la masse d'eau introduite à pour valeur m = 18 g
3. la constante d'équilibre de la réaction d'hydrolyse a pour valeur 0,6
4. l'acide sulfurique n'a pas déplacé l'équilibre de la réaction
5. l'acide sulfurique a déplacé l'équilibre de la réaction
On réalise la combustion d'un volume V = 200 L d'une espèce chimique gazeuse de formule brute CxHyNz en présence d'un excès de dioxygène. Le système chimique évolue jusqu'à un état final composé de 400 L de dioxyde de carbone, de 700 L d'eau, de 100 L de diazote et du dioxygène restant.

DONNEES : Toutes les espèces chimiques sont des gaz. Donc les conditions de l'expérience, le volume molaire des gaz est : Vm = 50 L.mol-1.

Quelle est la formule brute de l'espèce chimique étudiée ?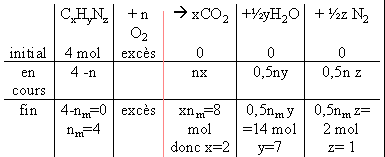
1. C2H6N
2. C2H6N2
3. C2H7N
4. C6H4N2
5. C6H7N
On considère les équation chimiques ci-dessous où A, B, D sont des espèces chimiques

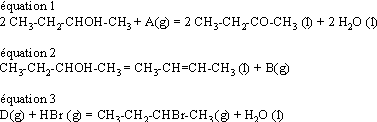
Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
1. le réactif A est le dioxygène
2. la réaction associée à l'équation 1 est une déshydratation
3. la réaction associée à l'équation 2 est une oxydation
4. la réaction associée à l'équation 3 est une substitution
5. le réactif D est le butan-2-ol
La législation actuelle autorise l'addition d'éthanol à l'essence à raison de 5% en volume d'éthanol. On traite 20 mL de ce carburant par une solution acidifiée de permanganate de potassium de concentration 0,4 mol.L-1. Seul l'éthanol réagit avec la solution oxydante. L'équivalence est obtenue après avoir versé 24 mL de solution oxydante.

DONNEES :
Couples redox mis en jeu : CH3COOH / CH3CH2OH et MnO4- / Mn2+
Masse volumique de l'éthanol : 790 kg.m-3
Masses molaires en g.mol-1 : H : 1 ; C : 12 ; O : 16.

Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
1. A l'équivalence, la couleur de l'essence passe de l'incolore au rose
2. la quantité de matière de l'éthanol est de 6.10^-3 mol dans les 20 mL d'essence
3. la quantité de matière de l'éthanol est de 1,2.10^-2 mol dans les 20 mL d'essence
4. le volume d'éthanol contenu dans un litre de carburant est de l'ordre de 70 mL
5. le carburant est conforme à la législation
On effectue le titrage de l'acide acétylsalicylique dans un comprimé d'aspirine. Cette quantité est égale à 500mg.
Pour cela, on utilise le mode opératoire suivant :
- on écrase le comprimé que l'on dissout ensuite dans un volume de 50 mL d'eau distillée, mesuré précisément à l'aide d'une fiole jaugée
- on prélève 18 mL de cette solution que l'on verse dans un becher
- on verse dans ce becher une solution d'hydroxyde de sodium de concentration 0,2 mol.L-1 jusqu'à obtenir l'équivalence. Le volume d'hydroxyde de sodium alors versé est égal à Ve.

DONNEE : La masse molaire de l'acide acétylsalicylique est M = 180 g.mol-1

Quelle est la valeur de Ve en mL ?
----> aide :
Qté de matière d'aspirine dans 18 mL : 0,5/180 *18/50 = 0,001 mol
à l'équivalence 0,001 = Ve*0,2
1. 5 mL
2. 8,5 mL
3. 11 mL
4. 13,8 mL
5. 15,2 mL
On étudie la cinétique d'une transformation chimique par la méthode spectrophotométrique.
A l'instant t = 0, on mesure l'absorbance d'une solution contenant 1 mL d'une solution d'iodure de potassium de concentration c1 = 9.10-3 mol.L-1 et 1 mL d'une solution d'eau oxygénée de concentration c2 = 5.10-2 mol.L-1 et quelques gouttes d'acide sulfurique.

DONNEE : Couples redox : I2 / I- et H2O2 / H2O

Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
1. l'absorbance du milieu réactionnel diminue au cours du temps
2. l'absorbance du milieu réactionnel augmente au cours du temps
3. le spectrophotomètre a été réglé sur une longueur d'onde correspondant à la couleur jaune
4. la vitesse de réaction à l'instant t=0 est nulle
5. au début de la transformation, il apparaît une couleur jaune
On mélange un volume V1 = 10 mL d'une solution d'acide éthanoïque de concentration C1 = 0,2 mol.L-1 et un volume V2 = 30 mL d'une solution de triméthylamine de concentration C2 = 0,1 mol.L-1.

DONNEES :
Couples acide-base CH3COOH / CH3COO- et (CH3)3NH+ / (CH3)3N
pKA1 (CH3COOH / CH3COO-) = 4,8
pKA2 ((CH3)3NH+ / (CH3)3N) = 9,9

Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
1. la valeur de la constante d'équilibre de la transformation est égale à 10^+5,1
2. la valeur de la constante d'équilibre de la transformation est égale à 10^ -5,1
3. l'avancement maximal de la transformation est égal à 3.10^-3 mole
4. la réaction est totale
5. le taux d'avancement finale est égal à 1
On réalise une pile à l'aide de deux solutions ioniques, de deux plaques métalliques et d'un pont salin.
Les solutions sont, pour l'une du sulfate de fer II de concentration C1 = 0,5 mol.L-1 et pour l'autre du sulfate de nickel II de concentration C2 = 10^ -7 mol.L-1. Les deux plaques métalliques sont en nickel et en fer. La plaque de fer plonge dans la solution de sulfate de fer et la plaque de nickel plonge dans la solution de sulfate de nickel. Le pont électrolytique est constitué par une solution de chlorure de potassium de concentration C3 = 0,01 mol.L-1.

DONNEES :
Couples redox constituants la pile : Fe2+ (aq) / Fe (s) et Ni2+ (aq) / Ni (s)
La constante d'équilibre K de la réaction Fe(s) + Ni2+(aq) = Fe2+ (aq) + Ni(s) est égale à 2.10^6.

Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
1. la plaque de fer est la borne positive
2. la plaque de nickel est la borne positive
3. il se produit une réduction dans la demi-pile " fer "
4. il se produit une oxydation dans la demi-pile " nickel "
5. la réaction se produisant dans la pile se traduit par l'équation : Fe(s) + Ni2+(aq) = Fe2+ (aq) + Ni(s)
On dispose d'un composé organique A de formule brute C4H8O2. Pour déterminer sa structure, on procède aux deux expériences suivantes :
- on traite le composé A avec de l'eau en excès en présence d'acide sulfurique, on obtient alors deux composés B et C
- on traite le mélange B et C par une solution acide de permanganate de potassium en excès, on obtient un seul produit organique B.

Quelle(s) est (sont) l'(les) affirmation(s) exacte(s) ?
----> aide :
hydrolyse d'un ester A donne un acide B et un alcool C
l'oxydation ménagée de C donne un acide carboxylique : donc C est un alcool primaire
1. le composé B est un alcool secondaire
2. la première expérience correspond à une réaction acido-basique
3. la deuxième expérience correspond à une réaction d'oxydo-réduction
4. l'acide contenu dans la solution acide de permangante de potassium est un catalyseur
5. le nom du composé A est l'éthanoate de propyle

d'après concours kiné ADERF 2004

Les calculatrices sont interdites.EPREUVE DE PHYSIQUE (Durée 1 heure - 20 points)EPREUVE DE CHIMIE (Durée 30 MINUTES - 10 points)

Les calculatrices sont interdites.

EPREUVE DE PHYSIQUE (Durée 1 heure - 20 points)
EPREUVE DE CHIMIE (Durée 30 MINUTES - 10 points)