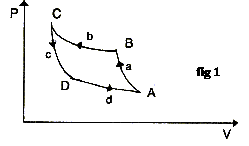
Le schéma de principe d'une machine à froid par compression peut être ramené à :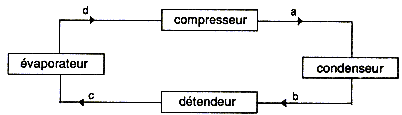

Le fluide caloporteur utilisé peut être considéré comme un gaz parfait de capacités thermiques molaires:

Cp = 35,61 J.mol^-1 K^-1 ; Cv = 27,30 J.mol^-1 K^-1 ; R = 8,31 J.mol^-1 K^-1 ; g= 1,304

Dans un premier temps, on suppose que le système fonctionne selon un cycle réversible entre les températures T_l = 269 K et T₃ = 298 K. Le cycle peut être alors schématisé dans le diagramme de Clapeyron par :

1. 
   où (a) et (c) sont deux adiabatiques réversibles, et (b) et (d) deux isothermes.

On appelle coefficient de performance la quantité e = Q_d/W où W représente le travail échangé avec le milieu extérieur au cours d'un cycle et Q_a, Q_b, Q_c, Q_d les quantités de chaleur échangées lors des étapes a, b, c, d du cycle.

1. Etablir que dans notre cas, ce coefficient devient e = T₁/(T₃-T₁).
2. Calculer ce coefficient.

Le système réel étudié maintenant peut être représenté par deux adiabatiques réversibles (a) et (c) et deux isobares (b) et (d), respectivement à P_l = 2.10⁵ Pa et P₂ = 7.10⁵ Pa.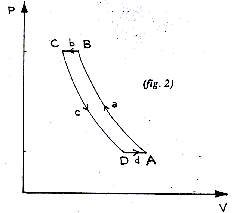

En régime permanent, la machine frigorifique est en liaison avec une source chaude à la température T₃ = 298 K et une source froide à la température T_l = 269 K.

1. Calculer le volume, la pression et la température à chaque étape du cycle.
   - Calculer le nombre de moles de fluide.
   - Ne pas oublier de recopier le tableau sur la copie avant de le compléter et de donner les formules littérales pour justifier les calculs faits.

   	A	B	C	D
   P(Pa)	2 105	7 105
   V(m3)	6 10-3
   T(K)	269		298
   n(mol)

2. Calculer le travail échangé par le fluide avec le milieu extérieur, au cours de chaque étape.
   - En déduire le travail échangé par le fluide avec le milieu extérieur au cours du cycle.
3. Calculer les quantités de chaleur Q_d et Q_b échangées par le fluide avec le milieu extérieur.
4. Calculer le coefficient de performance de la machine.

    

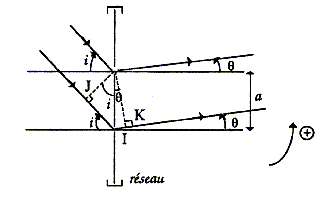
Un spectrogoniomètre classique à réseau comprend notamment les éléments suivants :

- un collimateur qui donne d'une fente source verticale une image à l'infini

- un réseau plan, par transmission, dont les traits sont verticaux et qui est éclairé par la lumière issue du collimateur

- une lunette autocollimatrice qui permet d'observer la lumière transmise par le réseau et dont la position angulaire repérée par rapport à la normale au réseau est lue sur un cercle gradué de 0° à 360° (alidade).

1. Etablir la relation fondamentale du réseau plan par transmission en précisant les conventions de signes utilisées. On respectera les notations de la figure simplifiée ci-dessous, on appellera n le nombre de traits du réseau par millimètre et a la distance entre deux traits voisins du réseau.
2. Pour déterminer n, le nombre de traits par millimètre caractéristique du réseau, on utilise une source de lumière monochromatique de longueur d'onde l = 589,3 nm. Le faisceau de rayons parallèles qui émerge du collimateur arrive sur le réseau sous incidence normale.
   - Comment peut-on s'assurer avec le spectrogoniomètre utilisé ici que l'on est bien en incidence normale ?
3. Le faisceau monochromatique donne naissance à des raies images dont on repère les positions angulaires par rapport à la normale au réseau. On constate que les directions des deux raies images d'ordre 1 et -1 forment entre elles un angle de 41°55'. Calculer n.
4. On utilise désormais une source polychromatique dont on veut mesurer les longueurs d'onde caractéristiques. On opère toujours sous incidence normale. On repère pour chaque longueur d'onde (couleur) la position des raies images dans le premier ordre à droite et à gauche.

   longueur d'onde	k=1	k=-1
   l1	196°10	165°27
   l2	200°12	161°26
   l3	201°17	160°20
   l4	201°22	160°15

   Calculer les longueurs d'onde l₁, l₂, l₃, l₄.
5. Pour mesurer la longueur d'onde correspondant à la raie violette on utilise la méthode dite du " minimum de déviation ". On éclaire ici le réseau sous une incidence variable et on repère les directions incidentes et transmises par rapport à la normale au réseau avec une convention d'orientation qui devra être précisée. Pour une longueur d'onde donnée, la déviation passe par un minimum lorsque l'angle d'incidence est égal, en valeur absolue, à l'angle de diffraction.
   - Donner pour un ordre fixé k l'expression de la déviation minimale D en fonction de n,l et k.
   On repère, dans l'ordre 1 les deux positions correspondant au minimum de déviation pour la raie violette ( l₅):
   longueur d'onde l₅ : k = 1 (194°53'); k = - 1 (166°43')
   Calculer la longueur d'onde l₅.

    

---

corrigé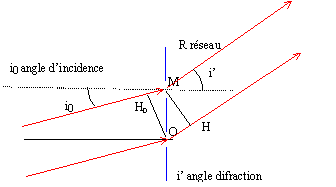

---

Les rayons incidents sont parallèles ainsi que les rayons réfractés..

La différence de chemin optique entre le rayon passant par le point O et celui passant par le point homologue M vaut ( l'indice de l'air vaut 1) : OM = a

OH-MH₀ = a sin i'- a sin i₀ = a( sini'-sin i₀) avec a = 1/n ; n pas du réseau en nombre de traits / m.

Le interférences sont constructives entre les ondes diffractées si la différence de marche est un multiple de la longueur d'onde l.

1/n ( sini'-sin i₀) = kl avec k entier positif, nul ou négatif

sin i'-sin i₀ = kl n.

---

 

---