|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
|||||||||||||||||
|
|||||||||||||||||
|
|
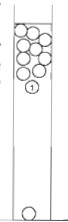
Cet exercice vise à comprendre le fonctionnement de ce
thermomètre. Cet objet décoratif est constitué d'une colonne remplie
d'un liquide incolore et de plusieurs boules en verre soufflé, lestées
par une petite masse métallique. Le liquide contenu dans la colonne a
une masse volumique r l(T) qui
décroît fortement lorsque la température augmente. Les boules ont
chacune le même volume mais possèdent des masses différentes. Un petit
médaillon indiquant une température est accroché sous chacune d'elles.
Chaque boule possède une masse ajustée de manière précise. Pour un
modèle commercial courant, on trouve onze boules indiquant des
températures comprises entre 17 °C et 27 °C. Principe de fonctionnement :
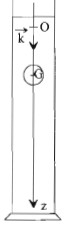
Étude du mouvement d'une boule :
|
||||||||||||||||
|
|
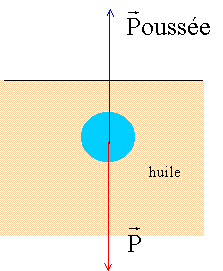
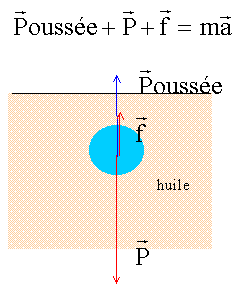
corrigé Principe de fonctionnement : Inventaire des forces s'exerçant sur la boule 1 : Poids, verticale vers le bas, valeur P=mg avec m=rVb g = 12 10-3*9,80 = 1,22 10-3 N Poussée d'Archimède, verticale, vers le haut, valeur F= r l(T)Vb
g
Expression littérale de la masse volumique r que doit avoir la boule 1 pour rester immobile : rVb g =r l(T)Vb g ; r =r l(T). Les autres boules ont des masses différentes et le même volume : donc leurs masses volumiques sont différentes de celle du liquide ; certaines boules restent les unes en haut de la colonne, les autres en bas. Lorsque la température du liquide s'élève, la boule 1 se met en mouvement : la masse volumique r l(T) du liquide décroît fortement, quand la température s'élève. En conséquence la valeur de la poussée d'Archimède diminue, devient inférieure à la valeur du poids ; celui-ci l'emporte et la boule descend.
Étude du mouvement d'une boule : Les forces s'exerçant sur la boule en mouvement :
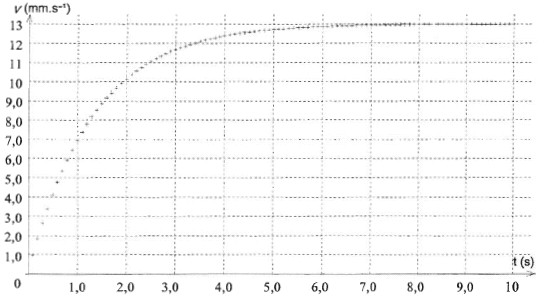
La deuxième loi de Newton, écrite sur un axe vertical orienté vers le bas donne : P-Poussée - f = mdv/dt de plus P= rVb g ; Poussée = r l(T)Vb g ; m = rVb rVb g - r l(T)Vb g - k v = rVb dv/dt. r g - r l(T) g - k/Vb v = r dv/dt ; dv/dt =( 1 - r l(T) /r)g - k/(Vbr) v. La vitesse v(t) du centre d'inertie de la boule obéit à une équation différentielle de la forme dv/dt= A - B.v . Expressions littérales de A et de B en fonction de m, g, k, r l(T) et Vb : A= ( 1 - r l(T) /r)g ; B= k/(Vbr) = k/m Expression littérale de la vitesse limite atteinte par la boule : Dès que la vitesse limite est atteinte, le mouvement devient rectiligne uniforme : dvlim / dt = 0 soit A - B.vlim =0 ; vlim = A/B = 9,5 10-3 / 7,3 10 -1 = 1,3 10-2 m/s. On se propose de résoudre l'équation différentielle dv/dt= A - B.v et de construire la courbe v = f(t) en utilisant la méthode d'Euler. Cette méthode itérative permet de calculer, pas à pas, de façon approchée, les valeurs de la vitesse instantanée de la boule à différentes dates. On utilise la relation suivante : v(tn) = v(tn-1) + Dv(tn-1) avec Dv(tn-1) = a(tn-1) . D t avec tn = tn-1 + Dt où D t est le pas d'itération du calcul. Dv(t0) =(A - B.v(t0)) D t = ( 9,5 10-3-7,3 10 -1*0) 0,1 =9,5 10-4 m/s v(t1) = v(t0) + Dv(t0) = 0 + 9,5 10-4 = 9,5 10-4 m/s Dv(t1) = ( 9,5 10-3-7,3 10 -1*9,5 10-4) 0,1 =9,5 10-4 m/s v(t2) = v(t1) + Dv(t1) = 9,5 10-4 +8,8 10-4 = 1,83 10-3 m/s Dv(t2) = ( 9,5 10-3-7,3 10 -1*1,83 10-3) 0,1 =8,2 10-4
m/s
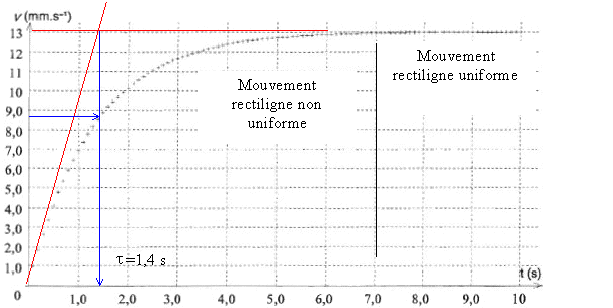
mouvement rectiligne non uniforme ou régime transitoire ; mouvement rectiligne uniforme ou régime permanent. L'abscisse de l'intersection de la tangente à l'origine avec l'asymptote horizontale donne le temps caractéristique t. ou bien à t = t la vitesse vaut 63% de la vitesse limite ; trouver l'abscisse du point correspondant. La valeur du pas utilisé doit être de l'ordre de t/10 : le choix 0,1 s est approprié ; c'est un
bon compromis entre une bonne précision ( assez de points pour tracer
la courbe) et un nombre de calculs pas trop grand. ( plus le pas est
petit, plus le nombre de calculs est grand)
|
||||||||||||||||
|
|