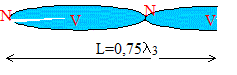|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||
|
||||
|
|
La technique utilisée pour jouer du didjeridoo est unique en comparaison de celle des autres instruments à vent. Il faut soufler dans le tube, les lèvres désserrées, pour créer un son : le bourdon, qui est le son de base du didjéridoo. En jouant avec les joues comprimées et la langue à l'avant de la bouche, un grand nombre de didjéridoos donneront un son comportant une variétés d'harmoniques subtiles qui ajoute couleur et richesse à l'effet d'ensemble. Partie 1 : Lorsqu'une onde stationaire s'établit dans un tuyau sonore, on observe un noeud ( N) de vibration à une extrémité si celle-ci est fermée, et un ventre (V) de vibration si cette extrémité est ouverte. En simplifiant on peut représenté le didjéridoo comme un tuyau sonore de longueur L fermé à une extrémité et ouvert à l'autre. Pour le mode fondamental de vibration, les positions du ventre et du noeud sont données sur la figure ci-dessous, schématisant l'amplitude de la vibration sonore.  célérité du son dans l'air : v = 340 m/s.
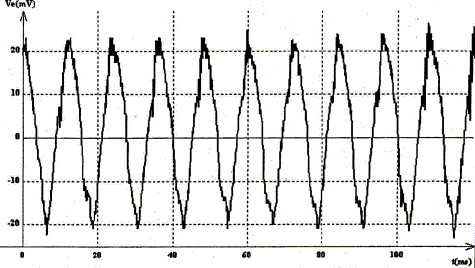
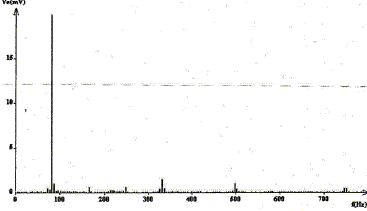
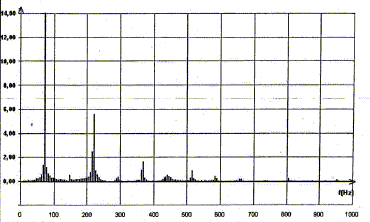
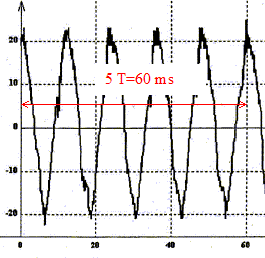
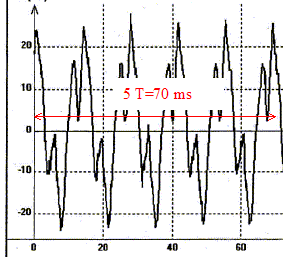
Partie 2 : Avec un second didjéridoo de longueur différente L', on enregistre un son dont l'oscillogramme et le spectre sont donnés.
Partie 3 : Un concert est donné avec les deux didjéridoos. Placés à deux mètres des musiciens, on mesure le niveau sonore L ' en décibel acoustique) produit successivement par chacun des instruments ; on note L1=72 dB et L2 = 75 dB. On rappelle que le niveau sonore est donné par la relation L= 10 log (I/I0) avec I0 intensité sonore de référence I0 = 10-12 W/m².
Les ondes sonores sont des ondes longitudinales : la direction de propagation est parallèle à la déformation du milieu ( propagation d'une variation de la pression ) Expression de la longueur d'onde l : La distance séparant deux noeuds consécutifs de vibration est égale à ½l ; la distance séparant un noeud et le ventre le plus proche vaut : 0,25 l. d'où l = 4 L fréquence f1 du mode fondamental : l = v/f1 = 4L soit f1 = v/(4L) avec v en m/s célérité de l'onde.
période T= 60/5 = 12 ms = 1,2 10-2 s ; f1 = 1/T = 100/1,2 = 83,3 Hz son grave. longueur L : 4L= v/ f1 ; L= 0,25 v/f1 = 0,25*340/83,3 = 1,02 m Longueur minimale d'un tuyau ouvert aux deux extrémités donnant un son de même hauteur : sons de même hauteur, donc sons ayant la même fréquence f1 du fondamental tuyau ouvert aux deux extrémités : il y a un ventre de vibration à chaque extémité ; la distance entre deux ventres consécutifs vaut ½l d'où la longueur du tuyau vaut L'=½l1 =½ v/f1 = 170 /83,3 = 2,04 m. fréquence du mode fondamental :
période T= 70/5 = 14 ms = 1,4 10-2 s ; f1 = 1/T = 100/1,4 = 71,4 Hz son grave. Longueur L' du second instrument :4L'= v/ f'1 ; L'= 0,25 v/f'1 = 0,25*340/71,4 = 1,19 m technique utilisée par l'instrumentiste : 2b : pratiquement pas d'harmoniques donc la technique utilisée est : souffler dans le tube, les lèvres desserrées 3b : son riche en harmoniques donc la technique utilisée est : joues comprimées et la langue à l'avant de la bouche rang n de l'harmonique ayant la plus grande amplitude : harmonique de rang 3 de fréquence f3=3f'1 ; (n=3) nœuds et ventre de vibration correspondant à cette harmonique :
f3 = 3 f'1 ( lecture graphe) ; or f=v/l d'où l 3 = l 1/3 ; L= 0,25 l 1 = 0,75 l 3 Relation entre L et le rang n de l'harmonique : fondamental ( ou harmonique de rang 1) n=1 alors L= 0,25 l1 soit 0,25(2n-1)l1
Intensités sonores : L= 10 log (I/I0) soit I=I0 10(L/10) I1 = 10-12 107,2 = 10-4,8 = 1,58 10-5 W/m² I2 = 10-12 107,5 = 10-4,5 = 3,16 10-5 W/m² I1+I2 =I = 4,74 10-5 W/m² L= 10 log(4,74 10-5 / 10-12)=76,8 dB
|
|||
|
|