|
Condensateur plan ( électrostatique ) En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|
| .
. |
|
|
|
|
Un plan infini porte une densité superficielle de charge s uniforme. Les caractéristiques du champ électrostatique créé par ce plan sont : 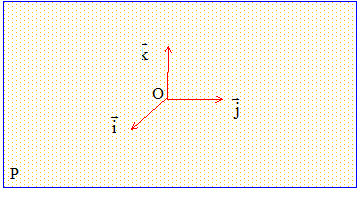 1.a) Montrer qu’il crée un champ électrique de la forme . ()xEExu=.... 1.b) Déterminer la fonction . ()Ex DS : électrostatique, page 1 2) Le plan (P1) d’équation porte une densité superficielle de charge uniforme et le plan (P/2xe=-s-2) d’équation porte une densité superficielle de charge uniforme. /2xe=s 2.a) Déterminer le champ électrique créé par ces deux plans dans tout l’espace. 2.b) Calculer la différence de potentiel . (/2)(/2)UVeVe=-- DS : électrostatique, page 2 e ) 3) En réalité, (P1) et (P2) ne sont chargés que sur deux carrés en regard de coté a ; ces deux carrés portent les charges et Q. Exprimer la capacité en fonction de ,a et e. ..Q-/CQU=0e 4) Calculer la force exercée par (P1) sur (P2). 5) Primitivement, , de sorte que les deux charges et Q sont confondues. Un opérateur agit sur Q, de sorte qu’il obtient la situation de la question 2). Quel est son travail ?
corrigé 1.a) La distribution de charge est invariante par translation perpendiculaire à l’axe Ox, donc , ce qui implique que ()VVx=gradxdVEVdx=-=-.............. u u .. = est de la forme Ex ()x 1.b) Le plan x est un plan de symétrie des charges, donc de : est une fonction impaire. 0E..()Ex Appliquons le théorème de Gauss à un cylindre de génératrices parallèles à l’axe Ox et clos par deux sections symétriques par rapport au plan chargé : 000si 022 si 0 2 x x x E u ES S x E u s .. > = .. = se . ........ < =-e se .. .. .. .. 2.a) En ajoutant les champs électriques produits par P1 et P2 : 0si 02si 22si 02xexEeexEexE<-=s-<<=-e>=............ u 2.b) /2/20xexeeUd V Edx = =- = = - = s . . e e = s 3) Puisque a, négligeons les effets de bord : Qa, ..20eU, d’où = s e 20QaC. U e = =e 4) 22212120022xxPaFdqEdSu..ss==s×-=-ee...........u . 5) 221202opopaeWF dr F. dr = · = - · = s . . e .. ...... .. ...... L’énergie du condensateur est 222020011222aeaeCUee.s.s..==......ee 2 ; elle est égale au travail de l’opérateur qui a séparé les charges. VII. 1) 2tancosadad.=..=..... ; 2221coscosaarr.=.=.. 2222000cos444cosdaddEara.....===pepepe... d. 2.a) []()[]()000/2/2000sinsincoscossin444coscossinsincos444xydEdEaaadEdEaaapßßaapßa-p....ß-a=.=.=.=pepepe....ß-a=-.=-.=.=pepepe.... 2.b) D’après l’expression de 1), les contributions au champ électrique de deux segments élémentaires situés dans des angles symétriques par rapport à la bissectrice de ont même grandeur ; comme elles ont des directions symétriques par rapport à la bissectrice, leur somme est dirigée selon la bissectrice. Le champ électrique total est donc parallèle à cette bissectrice. (,MAMBE.. 0x= E .. x -s /2e -e /2 s P1 P2 x . d. Ed.. d.. .. ) DS : électrostatique, page 7 |
|
|
|