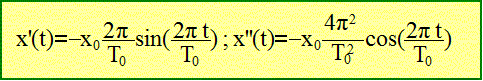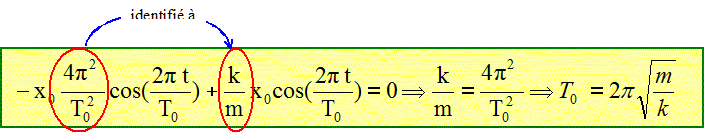|
Vibration d'une molécule de dioxyde de carbone ; effet de serre ; datation au carbone 14 bac S Antilles 09/07 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||
|
||||||
|
Vibration d'une molécule de dioxyde de carbone : La molécule de dioxyde de carbone est une molécule linéaire dont la représentation de Lewis est la suivante : Dans cette molécule, les atomes ne sont pas fixes, mais peuvent vibrer les uns par rapport aux autres. On peut ainsi modéliser cette molécule en considérant que les différents atomes de cette molécule sont des masses reliées entre elles par des ressorts, ressorts modélisant les deux liaisons chimiques. On aura ainsi le modèle suivant :
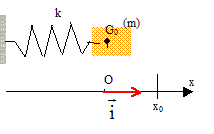
Pour simplifier davantage la mise en forme du problème, on considèrera que seuls les atomes d'oxygène sont en mouvement unidirectionnel par rapport à l'atome de carbone, qui lui, reste fixe. L'étude sera donc portée sur le mouvement d'un seul atome d'oxygène, oscillant librement sans frottement par rapport à un support fixe. L'action de la pesanteur est négligée dans cet exercice. Cette simplification conduit au modèle suivant : ( ressort de masse nulle et de raideur k)
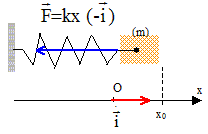
On se place dans un référentiel galiléen. On écarte la masse m de sa position d'équilibre (x=0) en lui donnant l'abscisse x0. La masse est alors abandonnée sans vitesse initiale. Quelle est le nom de l'unique force mise en jeu dans ce problème compte tenu des simplifications de l'énoncé ? Quelle est son expression littérale ? La représenter. Le ressort est allongé si l'abscisse x est positive. Il est rappelé par une force dite " force de rappel " vers sa position d'équilibre ( x=0, ressort non déformé). Cette force est proportionnelle à la déformation du ressort. La déformation, notée x, est égale à la longueur du ressort diminuée de sa longueur initiale. Cette force et le vecteur unitaire
i sont toujours de sens
contraire d'où :
En appliquant une loi dont on donnera le nom, établir l'équation différentielle vérifiée par la position x(t) de la masse m. Ecrire la deuxième loi
de Newton. Projection sur l'axe x : mx'' = -kx soit :
En considérant que l'expression Dériver deux fois x(t) par rapport au temps :
Repport dans l'équation différentielle :
T0 est la période.
En déduire l'expression littérale de la fréquence f0 des oscillations. A.N : k=422 N m-1 et m = 2,66 10-26 kg
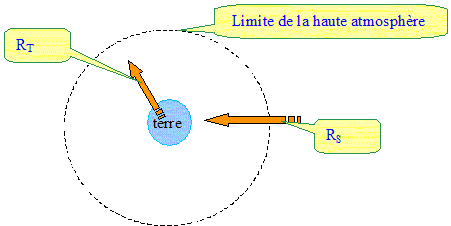
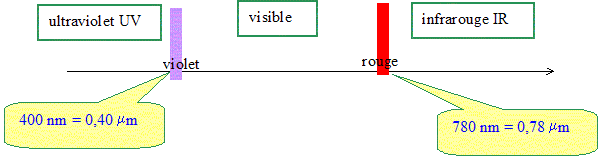
L'effet de serre est avnt tout un phénomène naturel. Il permet à notre planète de maintenir une température moyenne à la surface du globe de 15°C. Sans celui-ci, cette température moyenne serait de l'ordre de -18°C. Il existe un effet de serre additionnel, dù à l'importance des rejets en dioxyde de carbone, qui risque de compromettre l'équilibre climatique. Pour comprendre l'effet de serre, on retiendra la modélisation très simplifiée suivante : - une énergie thermique RS parvient à la surface de la terre sous lea forme de rayonnement électromagnétique solaire. Les fréquences de ces radiations sont celles du visible. - la terre recevant cette énergie doit la restituer vers l'espace. Cette restitution d'énergie RT se fait sous la forme d'un rayonnement électromagnétique terrestre, essentiellement situé dans l'infrarouge. L'équilibre est assuré lorsque RS=RT. - l'atmosphère peut alors jouer un rôle de couvercle pour ces radiations en absorbant les radiations RT retenant ainsi l'énergie émise par la terre et la réémettant vers l'espace. Le dioxyde de carbone intervient dans ce processus. Rappeler sur un axe gradué en longueur d'onde, les valeurs limites du spectre visible dans le vide, ainsi que les couleurs associées à ces limites. Ces valeurs seront données en micromètres ( mm ) et en nanomètres ( nm ). Nommer et situer les domaines de radiations situés au delà de ces limites.
Pour une onde électromagnétique dans le vide, quelle relation littérale relie sa longueur d'onde l0, sa fréquence f et sa célérité c ? l0 = c/f avec l0 en mètre, f en hertz et c en m s-1.
Par la suite on prendra c = 3,00 108 m/s. Pour comprendre les vibrations de la molécule de dioxyde de carbone, il faut considérer qu'elle absorbe certaines radiations électromagnétiques susceptibles de la mettre en mouvement vibratoire. Si la fréquence du rayonnement électromagnétique est la même que la fréquence propre de vibration mécanique, alors il y a absorption de ce rayonnement. La fréquence propre de vibration de la molécule de dioxyde de carbone vaut f0=2,00 1013 Hz. Déterminer la longueur d'onde l0 ( en mm) du rayonnement électromagnétique correspondant que peut absorber le dioxyde de carbone. l0 = c/f0 = 3,00 108 / 2,00 1013 = 1,50 10-5 m = 1,0 10-6 m = 15,0 mm. Dans quelle gamme du spectre se situe la longueur d'onde calculée ? 15 mm , valeur supérieure à 0,78 m m, se situe dans l'infrarouge. Expliquer pourquoi le dioxyde de carbone atmosphérique peut piéger l'énergie thermique émise par la surface de la terre. L'atmosphère émet un rayonnement infrarouge ; ce dernier est évacué vers l'espace. Mais le dioxyde de carbone absorbe une partie du rayonnement émis par la Terre. Ce gaz à effet de serre restreint donc la transmission du rayonnement infrarouge vers l'espace.
Des pingouins
à Marseille !
Dans la haute atmosphère un atome d'azote du diazote atmosphérique N2 est soumis à un rayonnement de neutrons. Lorsqu'un neutron entre en collision avec un atome d'azote, il s'en suit la formation d'un atome de carbone 14 et d'une autre particule que l'on nomme X. On a ainsi l'équation suivante : 10n + 147N -->146C + AZX. Enoncer les lois de conservation relatives à une transformation nucléaire. En déduire l'identité de la particule X. Conservation de la charge : 7 = 6+Z d'où Z= 1 Conservation du nombre de nucléons : 1+14 = 14 + A d'où A = 1 La particule X est un proton 11H.
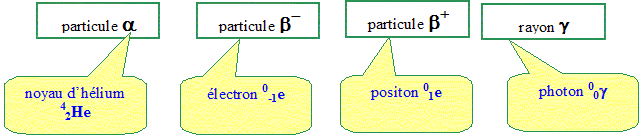
L'atome de carbone 14 ainsi produit se retrouve dans une molécule de dioxyde de carbone. Cette molécule peut être assimilée par un organisme végétal grâce à la photosynthèse. Tant que l'organisme est vivant, sa teneur en carbone 14 par rapport à l'isotope majoritaire carbone 12 reste constante. C'est à la mort de l'organisme que ce taux diminue en raison du caractère radioactif du carbone 14. Qu'est-ce qu'un noyau radioactif ? Un noyau radioactif est un noyau instable : il se transforme en d'autre(s) noyau(x) plus stable(s) ; cette désintégration s'accompagne de l'émission de rayonnements. Citez les quatre type d'émissions qui caractérisent la radioactivité.
Sachant que le carbone 14 présente une radioactivité b-, écrire l'équation traduisant sa désintégration. 146C-->147N + 0-1e. En 1991, un plongeur amateur découvre près de Marseille l'ouverture d'une grotte sous marine située à 37 m sous le niveau de la mer. En remontant la grotte, il y trouva des cavités présentant des peintures rupestres, avec entre autres animaux des pingouins ! L'analyse du charbon ayant servi à ces peintures montre que le taux de carbone 14 présent n'est que de 9,20 % par rapport à celui trouvé dans un organisme vivant. On donne la demi-vie t½ du carbone 14 : 5370 ans. Rappeler la définition de la demi-vie. Durée au bout de laquelle la moitié des noyaux radioactifs initiaux se sont désintégrés. On rappelle également la loi de décroissance radioactive N(t) = N0 exp(-lt) avec l t½=ln2. Quel nom donne t-on à la constante l ? Quelle est son unité compte tenu des données de l'énoncé ? l est la constante radioactive du carbone 14. l est l'inverse d'un temps ; la demi vie t½ est donné en années ; l s'exprimera en an-1. Que vaut le rapport N(t) / N0 ? " le taux de carbone 14 présent n'est que de 9,20 % par rapport à celui trouvé dans un organisme vivant " N(t) / N0 =9,20 10-2.
Quel est l'âge de ces peintures ? 9,20 10-2 = exp(-lt) ; ln(9,20 10-2 ) = -lt avec l =ln2 / t½. ln(9,20 10-2 ) = - t ln2 / t½ t = ln(9,20 10-2 ) / ln2 * t½ t = ln(9,20 10-2 ) / ln2 * 5730 = 1,97 104 ans. On sait aujourd'hui que l'accroissement de l'effet de serre lié aux activités humaines risque de compromettre l'équilibre pour le siècle à venir. Un des risque majeurs serait une augmentation de température moyenne à la surface de la terre, avec entre autres conséquences une fonte partielle des glaces polaires. Que peut traduire la présence de ces animaux dans ces grottes quant aux climat de cette époque ? A cette époque le climat régnant à Marseille devait ressembler à celui du cercle polaire. Pourquoi la grotte était-elle accessible aux hommes ? Une grande partie du continent européen devait être recouvert par les glaces. Un plus grande partie de l'eau ( par rapport à aujourd'hui ) se trouvait sous forme de glaciers continentaux . En conséquence, le niveau des mers était bien inférieur à celui de notre époque. |
||||||
|
|
||||||
|
|
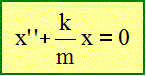
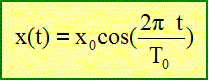 est solution de cette équation
différentielle,
déterminer l'expression littérale de
T0 en fonction de k et m. Quel est le nom de
cette grandeur ?
est solution de cette équation
différentielle,
déterminer l'expression littérale de
T0 en fonction de k et m. Quel est le nom de
cette grandeur ?