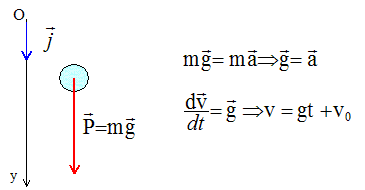|
chimie : acide chlorhydrique et magnésium ; mouvement ascendant d'une bulle de dihydrogène ; chute d'une bille d'acier dans l'air bac Nlle Calédonie 2007 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
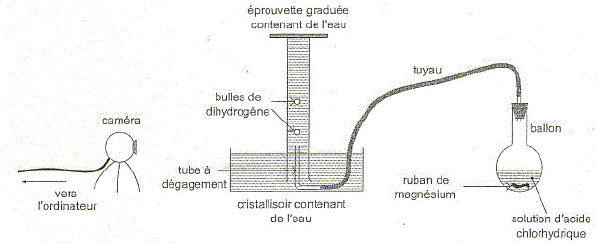
Dans le cadre d'un atelier scientifique ayant pour thème " espace et mouvement", trois élèves s'interrogent sur les expériences qu'ils vont effectuer pour étudier des mouvements rectilignes : Elodie :" nous devrions étudier un mouvement ascendant et un mouvement descendant". Arthur :" j'ai une idée. Pour étudier le mouvement ascendant nous pourrions filmer le mouvement dans l'eau de bulles de gaz ". Charlotte :" Et si par exemple nous filmions le mouvement ascendant de bulles d'hydrogène produites par réaction de l'acide chlorhydrique avec le magnésium ?" Arthur : " Et ensuite, pour comparer, nous pourrions filmer le mouvement d'une bille métallique lâchée dans l'air ". A l'aide d'une caméra reliée à un ordinateur, les élèves filment la transformation chimique entre l'acide chlorhydrique et le magnésium produisant du dihydrogène. Le schéma de l'expérience est reproduit ci-dessous :
Etude de la transformation chimique. A l'instant t=0 s, le ruban de magnésium est mis en contact avec la solution d'acide chlorhydrique. Solution d'acide chlorhydrique : c =0,50 mol/L ; V= 40 mL. Magnésium : m = 0,12 g ; Masse molaire M= 24 g/mol. Volume molaire des gaz dans les conditions de l'expérience : Vm= 24 L/mol. L'équation de la réaction associée à la transformation chimique qui a lieu dans le ballon s'écrit : Mg(s) + 2H+(aq) = Mg2+(aq) + H2(g). Identifier les couples oxydant / réducteur mis en jeu dans cette réaction. Mg2+(aq) / Mg(s). H+(aq) / H2(g).
A partir des quantités de matière initiales montrer que l'avancement maximal est xmax = 5,0 10-3 mol .
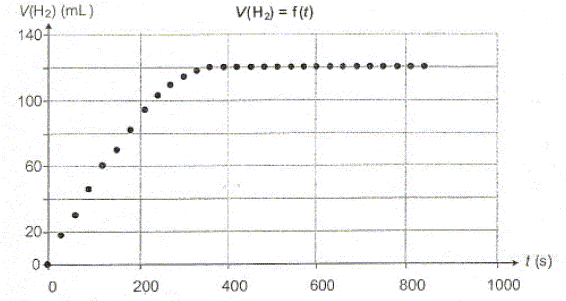
si H+ est en défaut : 2,0 10-2-2xmax =0 soit xmax =1,0 102 mol On retient la plus petite valeur : xmax =5,0 10-3 mol. La figure ci-dessous représente la variation de la valeur du volume de dihydrogène dégagé au cours du temps.
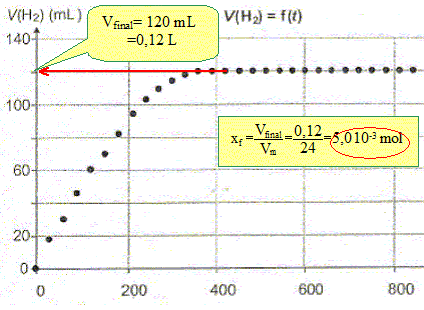
Déterminer graphiquement la valeur du volume de dihydrogène à létat final et en déduire l'avancement final xf de la réaction.
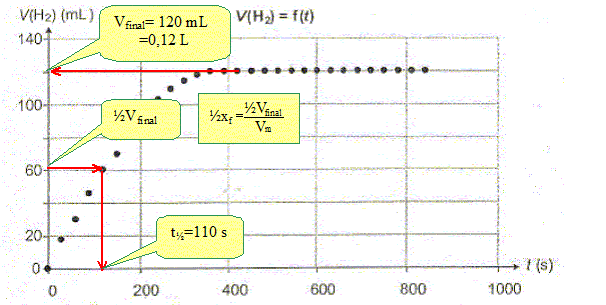
La transformation est-elle totale ? Justifier. Le taux d'avancement final t vaut : t = xf/xmax = 1 en conséquence la transformation est totale. Définir puis déterminer graphiquement le temps de demi-réaction t½. Le temps de demi réaction est la durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final. L'avancement et le volume de dihydrogène étant proportionnels, à t=t½, VH2 =60 mL.
Afin de mieux suivre le mouvement ascendant des bulles de dihydrogène dans l'éprouvette graduée, on souhaite augmenter le temps de demi-réaction. Proposer une méthode. Il faut diminuer la vitesse de la réaction : par exemple en travailant à une température plus faible ( vers 0°, en plaçant le mélange réactionnel, le ballon, dans un bain d'eau glacée).
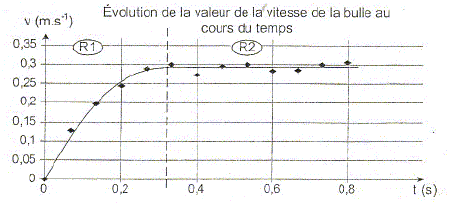
Etude d'u mouvement ascendant d'une bulle de dihydrogène. Après avoir purger le dispositif pour chasser l'air, on surmonte le tube à dégagement d'une éprouvette graduée contenant de l'eau. Le film vidéo obtenu à la fin de l'expérience est analysé à l'aide d'un logiciel de pointage. On choisit une nouvelle origine des dates à l'aide du logiciel. On peut donc suivre image par image, la position du centre d'inertie Gi à l'instant de date ti d'une bulle d'hydrogène au cours de son ascension dans l'éprouvette graduée. Le mouvement de la bulle s'éffectue suivant la direction verticale d'axe Oz, orienté vers le haut. On néglige les variations de pression dans l'éprouvette. Le dihydrogène est pratiquement insoluble dans l'eau : on peut donc considérer le volume d'une bulle comme constant. On note : VB : volume d'une bulle de dihydrogène ; masse volumique du dihydrogène r = 0,083 kg m-3. masse volumique de l'eau r0 = 1,0 10-3 kg m-3 ; intensité de la pesanteur g. Evolution de la vitesse au cours du temps. Les mesures successives de la coordonnée z(t) sont exploitées à l'aide d'un tableur-grapheur. On obtient la courbe suivante où R1 et R2 désignent les deux régimes successifs observés lors du mouvement.
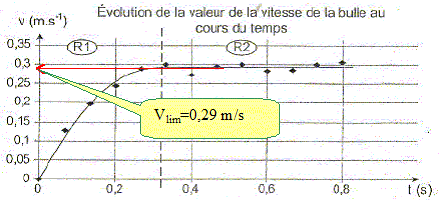
Quel nom donne t-on au régime R2 ? La vitesse limite est atteinte et reste constante. Il s'agit du régime permanent : le mouvement de la bulle est rectilligne uniforme. Déterminer graphiquement la valeur de la vitesse limite vlim.
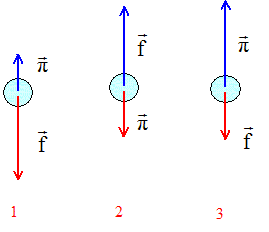
Bilan des forces. Donner l'expression de la valeur p de la poussée d'Archimède, due à l'immersion de la bulle dans l'eau, en utilisant les notations données. La poussée d'Archimède est égale au poids du volume d'eau d'éplace p = r0gVB. P désigne la valeur du poids de la bulle. Déduire du rapport P/p, exprimé en fonction de r et r0, que l'on peut négliger le poids de la bulle devant la poussée. poids P = mg avec m = r VB P/p = r / r0 =0,083/1000 = 8,3 10-5. Le poids est donc négligeable devant la poussée d'Archimède. Lors du mouvement de la bulle de dihydrogène, on ne considère donc que deux forces : la poussée d'Archimède et une force de frottement fluide ( notée f), de même direction et de sens opposé au vecteur vitesse v et dont la valeur augmente avec la vitesse. Parmi les trois représentations suivantes des forces exercées sur la bulle pendant le régime R1, choisir celle qui est correcte et justifier.
La vitesse a le sens du mouvement : verticale vers le haut ; la force de frottement fluide est en conséquence dirigée vers le bas : (2) est exclu. Le mouvement est ascendant et la vitesse augmente : le vecteur accélération est vertical ascendant. Or d'après la seconde loi de Newton, la somme vectorielle des forces et l'accélération sont colinéaires et de même sens. La somme vectorielle des forces est dirigée vers le haut : (1) est exclu. Donc schéma (3). Que peut-on dire de ces forces lorsque le régime R2 est atteint ? Justifier. En régime permanent la vitesse est constante : le mouvement est rectiligne uniforme. D'après le principe d'inertie, la bulle est pseudo-isolée ( la somme vectorielle des forces est nulle)
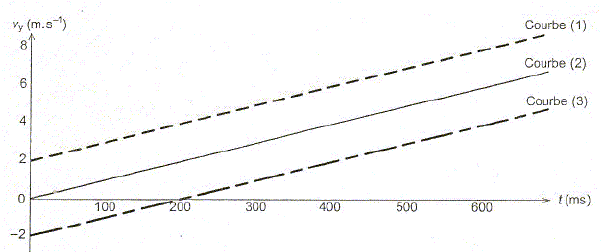
Etude du mouvement vertical d'une bille d'acier dans l'air : Les élèves étudie le mouvement vertical du centre d'inertie G d'une bille d'acier de masse m dans l'air. Les frottements et la poussée d'Archimède peuvent être négligés lors de ce mouvement. Le repère d'étude choisi est l'axe Oy verticale descendant. A l'instant initial le vecteur vitesse est v0, vecteur vertical. Quel nom donne t-on à ce type de mouvement ? La bille d'acier n'est soumise qu'à son poids : le mouvement est une chute libre. En appliquant la seconde loi de Newton à la bille, établir l'expression de la vitesse v en fonction du temps. Parmi les courbes suivantes pouvant représenter la vitesse, choisir celle qui corrspond à chacune des conditions initiales proposées. Justifier.
La bille est lâchée sans vitesse initiale. v= gt, fonction linéaire passant par l'origine O : courbe 2. La bille est lancée verticalement vers le haut. v = gt-v0. La vitesse initiale a le sens contraire de l'axe. L'ordonnée à l'origine est négative : courbe 3. La bille est lancée verticalement vers le bas. v = gt+v0. La vitesse initiale a le sens de l'axe. L'ordonnée à l'origine est positive : courbe 1. La présentation orale du projet scientifique. Lors de la présentation orale, l'un des spectateur pose la question suivante : "Vous avez étudié la chute d'une bille. Pourriez vous décrire la chute de deux objets, l'un étant beaucoup plus lourd que l'autre, dans un tube dans lequel on a préalablement fait le vide." Arthur : " l'objet lourd tombera plus vite que l'objet léger. Que pensez-vous de la réponse d'Arthur ? La réponse d'Arthur est fausse. En absence d'air dans le tube, la poussée d'Archimède et la force de frottement fluide due à l'air, sont nulles. Les objets n'étant soumis qu'à leur poids ont le même mouvement de chute libre.
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|