Aurélie 04/06/07
 

bac S Amérique Nord 2007 : rétroprojecteur, lentille, loupe, miroir plan. ( 4points) 

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

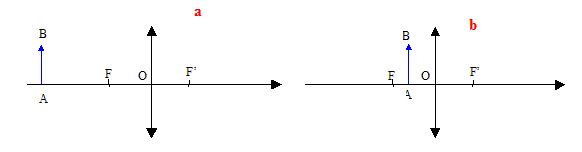
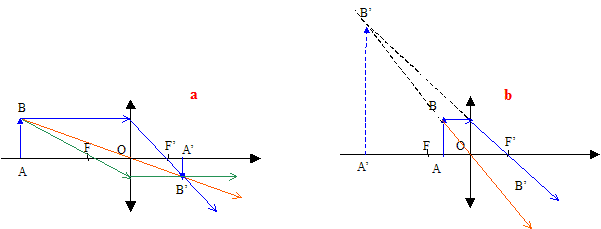
Différents usages d'une lentille mince

Construire les images de l'objet AB dans les situations (a), (b). Les foyers objet et image sont notés F et F'.

 

Les situations (a), (b) illustrent le fonctionnement de deux instruments d'optique : la loupe et l'appareil photographique.

Quelle situation correspond au fonctionnement de la loupe ? Justifier.

 

La situation b illustre le fonctionnement de la loupe : image virtuelle, droite, plus grande que l'objet.

La situation a illustre le fonctionnement de l'appareil photo : image réelle ( sur la pellicule) plus petite que l'objet.
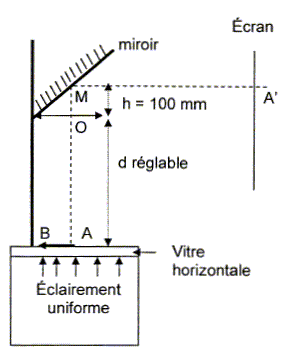
Donnée du constructeur : distance focale de la lentille : 315 mm

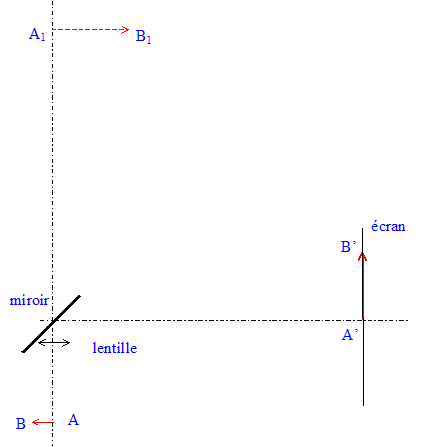
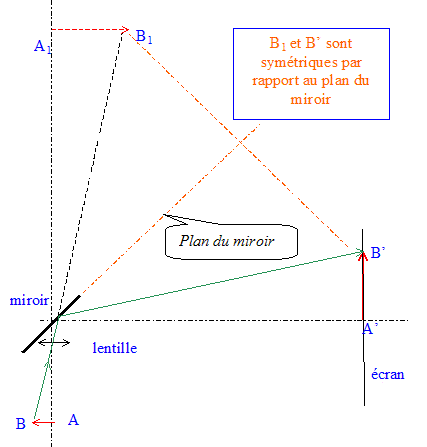
La lentille L donne une image intermédiaire A1B1 d'un objet AB et le miroir plan fournit une image définitive A'B' sur l'écran. Le centre optique O de la lentille est situé à une distance h = 100 mm du point M du miroir. Lorsque la distance OA = d réglable est fixée à OA = d = 400 mm, on obtient une image définitive

A'B' sur un écran placé à une distance MA' = 1,40 m. ( M : centre du miroir )

Le schéma correspondant à cette situation est représenté ci-dessous ; y sont représentés l'objet AB, l'image intermédiaire A1B1 et l'image définitive A'B'.

  1. Construire, sur le schéma donné en annexe le trajet suivi par un rayon lumineux issu de B et passant par le centre optique O de la lentille L.
  2. On étudie l'image intermédiaire A1B1. Quel rôle joue l'image intermédiaire A1B1 pour le miroir ?
    - Justifier la position de l'image intermédiaire A1B1 sur le schéma donné en     annexe.
    - Définir le grandissement     g pour l'image intermédiaire A1B1 donnée par la lentille L. Le déterminer en utilisant le schéma donné en annexe.
    - En utilisant les données numériques du texte retrouver, par le calcul, la     distance focale de la lentille L. Le résultat est-il conforme avec la donnée du constructeur ?
  3. On veut maintenant effectuer la projection du même objet AB sur un écran vertical placé à une distance MA1' = 4,00 m du miroir. Pour cela on règle la distance d à une nouvelle valeur d2 de OA. Calculer la valeur de d2 permettant d'obtenir une image nette sur l'écran. En déduire l'évolution de la distance d lorsque la distance miroir-écran augmente. 
 

 

Trajet suivi par un rayon lumineux issu de B et passant par le centre optique O de la lentille L :

Rôle joué par l'image intermédiaire A1B1 pour le miroir :

A1B1 joue le rôle d'objet virtuel pour le miroir.
Position de l'image intermédiaire A1B1 sur le schéma donné :

D'une part A1 et A', et d'autre part B1 et B' sont symétriques par rapport au plan du miroir.
Grandissement g pour l'image intermédiaire A1B1 donnée par la lentille L :

On écrit en bleu et en gras les distances algébriques.

g = OA'1/OA = -1,5 / 0,4 = -3,7.

Distance focale de la lentille L :

Ecrire la formule de conjugaison pour la lentille L : 1/OF' = 1/OA'1 - 1/OA

avec OA = -0,4 m et OA'1 = 1,5 m

1/OF' =1/1,5 + 1/0,4 =0,667 + 2,5 = 3,167 m-1.

OF' = 1/3,167 = 0,316 m.

On retrouve bien l'indication du constructeur.

On veut maintenant effectuer la projection du même objet AB sur un écran vertical placé à une distance MA1' = 4,00 m du miroir. Pour cela on règle la distance d à une nouvelle valeur d2 de OA.

Valeur de d2 permettant d'obtenir une image nette sur l'écran :

OA = -d2 m ; OA'1 = 4,1 m ; OF' =0,315 m

Appliquer à nouveau la formule de conjugaison :

1/OF' = 1/OA'1 - 1/OA

1/OA = 1/OA'1 -1/OF' =1/4,1 - 1/0,315 = 0,244 -3,167 = -2,92

OA = -1/2,92 = -0,342 m ; d2 = 0,34 m.

Evolution de la distance d lorsque la distance miroir-écran augmente :

La distance d diminue lorsque la distance miroir-écran augmente.

 
 
retour -menu