Un cycliste monte une côte à la vitesse moyenne v₁=12 km/h, puis redescend la côte aussitôt après à la vitesse moyenne v₂ = 36 km/h. Quelle est la vitesse moyenne ( km/h) du cycliste sur tout le parcours ? ( 16 ; 18 ; 20 ; 22 ; 24 )

Une voiture de masse m = 800 kg roule sur une route rectiligne horizontale. A la date t=0, le chauffeur coupe le moteur, la vitesse étant alors v₀ = 6 m/s. La résultante des forces de frottements est une force F constante, parallèle à la trajectoire. La voiture s'immobilise en 12 s. Quelle est la distance (m) parcourue par la voiture ? ( 18 ; 36 ; 72 ; 90 ; 108 )

Un solide ponctuel (S) de masse m = 100 g se met à glisser sans vitesse initiale et sans frottement du sommet d'une sphère de diamètre d = 120 cm. A quelle vitesse (m/s) décolle t-il de la sphère ? ( 1,5 ; 2,0 ; 2,8 ; 4,0 ; 7,8 )

---

 corrigé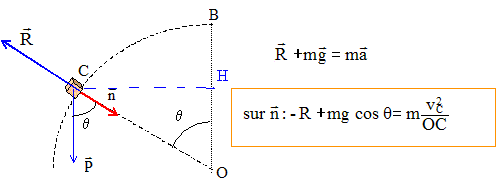

---

R= m[g cos q -v²_C/OC]

au moment du décollage, l'action du sol s'annule, R=0 soit : g cos q =v²_C/OC ; v²_C =g OCcos q. (1)

Théorème de l'énergie cinétique entre B et C :

L'action du sol, perpendiculaire à la vitesse, ne travaille pas.

travail moteur du poids : mgBH = mgOB(1-cos q)

½mv²_C-0 =mgOB(1-cos q) ; ½v²_C-0 =gOB(1-cos q) ;

1-cos q =v²_C/(2gOB) =v²_C/(2gOC) ; cos q =1-v²_C/(2gOC) ; g OCcos q =gOC-½v²_C.

repport dans (1) : v²_C = gOC-½v²_C ; 1,5v²_C = gOC ; v²_C =gOC / 1,5

v²_C = 9,8*0,6/1,5 =3,92 ; v_C = 1,98 m/s ( 2 m/s).

---

Une fronde est constituée d'un solide de masse m=150 g attaché à une extrémité d'une cordelette inextensible et de masse négligeable dont l'autre extrémité est tenue à la main. On fait tourner la fronde verticalement de manière à ce que le solide décrive à vitesse constante un cercle de rayon r= 49 cm.

Quelle doit être la vitesse angulaire de rotation ( rad/s) de la fronde pour que la tension de la cordelette soit égale au triple du poids quand le solide passe au point le plus bas de la trajectoire. ( 4,5 ; 5,0 ; 6,3 ; 7,7 ; 8,9 )

---

 corrigé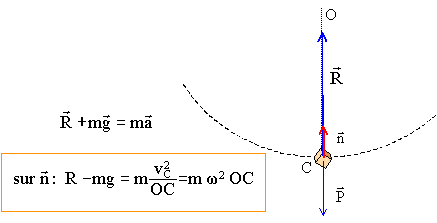

---

De plus R = 3 mg d'où : 2mg = mw²OC soit : w² =2 g/OC = 2*9,8 / 0,49 = 40 ; w = 6,3 rad/s.

---

Un ressort de raideur k, de longueur à vide L₀, de masse négligeable, à une de ces extrémités fixées à un point O. A l'autre extrémité du ressort est accroché un solide de masse m. L'ensemble tourne à vitesse angulaire constante dans un plan horizontal, le solide décrivant une trajectoire circulaire de centre O. Quelle est la longueur L du ressort en mouvement ?

kL₀ / (k-mw) ; kL₀ / (mw²-k) ; kL₀ / (mw²+k) ; L₀ / (-mw²+k) ; kL₀ / (-mw²+k)

---

 corrigé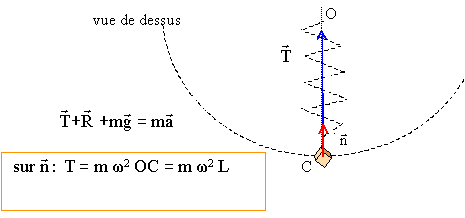

---

Or T= k( L-L₀) ; par suite : k( L-L₀) = mw²L

L( k-mw²) = kL₀ ; L = kL₀ / (k-mw²).

---

Une fusée de masse m = 2 t, soumise à la seule attraction terrestre, est en mouvement circulaire de rayon r = 7000 km autour de la Terre ( M= 6,0 10²⁴ kg , R = 6380 km), à la vitesse constante v₁ = 7561 m/s. G = 6,67 10^-11 S.I.

Quelle doit être la poussée F des moteurs pour que la fusée ait, sur la même trajectoire, une vitesse constante v₂= v₁ + 10 m/s ?

Quelle(s) est (sont) le(s) affirmation(s) exacte(s) ?

1. tangente à la trajectoire, dans le sens du mouvement, valeur 43,2 N.
2. tangente à la trajectoire, dans le sens du mouvement, valeur 1,37 kN.
3. radiale, vers le centre de la Terre, valeur 43,2 N.
4. radiale, vers le centre de la Terre, valeur 1,37 kN.
5. le mouvement étant uniforme, F est nulle.

La lune, satellite naturel de la Terre est assimilée à un point matériel de masse M_L. Dans le référentiel géocentrique, la lune soumise à la force de gravitation terrestre, décrit une trajectoire circulaire de centre O, centre de la Terre, et de rayon r, distance du centre de la terre au centre de la lune.

G= 6,67 10^-11 S.I ; R_T= 6380 km ; M_T= 6,0 10²⁴ kg ; M_L= 7,4 10²² kg. période de la lune T_L= 27 j 7 h 30 min.

Quelle est la valeur de r ( km) ?( 156 000 ; 280 000 ; 312 000 ; 384 000 ; 560 000 )

Deux plaques A et B planes, horizontales et parallèles, distantes de d= 6 cm sont soumises à une différence de potentielle U_AB= 90 V. B est reliée à la masse. Quel est le potentiel électrique V_C( volt), par rapport à la masse, en un point C situé entre les plaques à une distance y = 2 cm de la plaque A ? ( -60 ; -30 ; 30 ; 60 ; 0 )

Quelle(s) est (sont) le(s) affirmation(s) exacte(s) ?

1. Les lignes de champ magnétique sont orientées approximativement du Sud vers le Nord de la Terre ( vrai )
2. En France une aiguille aimantée pouvant tourner, à la fois autour d'un axe vertical et d'un axe horizontal, s'oriente dans une direction ni horizontale, ni verticale ( vrai )
3. En France la composante horizontale du champ magnétique terrestre vaut, à 10 % près, 2 10⁵ T ( faux : c'est 2 10^-5 T)
4. Le champ magnétique terrestre est pratiquement uniforme sur toute la surface de la Terre. ( faux)
5. A l'équateur le champ magnétique terrestre est pratiquement nul. ( faux)

On fait agir un champ magnétique uniforme de valeur B, perpendiculaire au plan xOy, sur un électron dans une région limitée de l'espace définie par 0<=x<= L

Un électron, de masse m, de charge q=-e, est introduit en O avec une vitesse v₀ selon Ox. A la sortie du champ magnétique, l'électron est dévié, par rapport à sa position initiale, d'un angle a petit. Quelle est l'expression de aa ( rad) ?

eLB/(mv₀²) ; eLB/(mv₀) ; mv₀B/ (eL) ; meL/v₀² ; mLB/(ev₀²)

---

 corrigé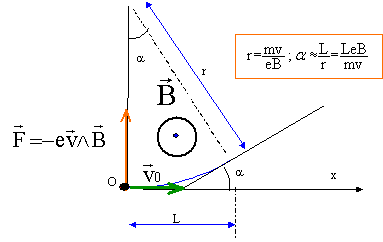

---

Une particule de masse m et de charge q entre dans une région de l'espace où règne un champ magnétique uniforme de valeur B avec une vitesse v₀ perpendiculaire au champ B.

Quelle(s) est (sont) le(s) affirmation(s) exacte(s) ?

1. Le mouvement de la particule est uniforme.
2. Le vecteur accélération est nul.
3. Le vecteur accélération est constant.
4. La particule a un mouvement dans le plan contenant le champ et perpendiculaire à la vitesse.
5. Si la vitesse augmente, le rayon de la trajectoire diminue.

Une plaque métallique de masse m est posée horizontalement sur quatre ressort identiques placés verticalement, chaque ressort a une raideur k. La plaque effectue des oscillations périodiques autour de sa position d'équilibre avec la période T₀ ; son mouvement se fait suivant une translation verticale.

Quelle est l'expression de la période ? 2p[m/k]^½ ; 2p[4m/k]^½ ; 2p[m/(4k)]^½ ; 2p[4k/m]^½ ; 2p[mk]^½ .

La différence de potentiel entre un nuage et le sol terrestre est de 7,0 10⁶ V. Au cours d'un éclair, de durée 0,01 s, une charge électrique passe du nuage dans le sol, en dissipant une énergie de 3,5 10⁸ J. Quelle est l'intensité électrique moyenne ( A) du courant qui a circulé entre le nuage et le sol ? ( 0,50 ; 1,0 ; 500 ; 5,0 kA ; 10 kA ).

Deux résistances R₁ et R₂ consomment les puissances respectives P₁ = 2,0 W et P₂ = 5,0 W lorsqu'elles sont soumises séparément à une tension constante de 6,0 V. Ces deux résistances sont associées en série avec un générateur délivrant la tension U= 12,0 V. On note respectivement I₁ et I₂ les intensités et U₁ et U₂ les tensions aux bornes de R₁ et R₂.

Quelle est la bonne réponse ?

1. I₁ = 0,33 A ; I₂ = 0,83 A ; U₁ = U₂ = 6,0 V.
2. I₁ = 0,34 A ; I₂ = 0,34 A ; U₁ = U₂ = 6,0 V.
3. I₁ = 0,86 A ; I₂ = 0,86 A ; U₁ = U₂ = 6,0 V.
4. I₁ = 0,48 A ; I₂ = 0,48 A ; U₁ =3,4 V ; U₂ = 8,6 V.
5. I₁ = 0,48 A ; I₂ = 0,48 A ; U₁ =8,6 V ; U₂ = 3,4 V.

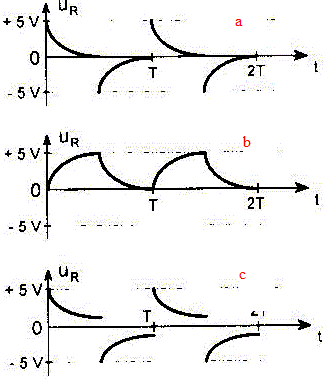
Un générateur est associé avec une résistance R et un condensateur C. La tension u_G délivrée par le générateur est représentée ci-dessous :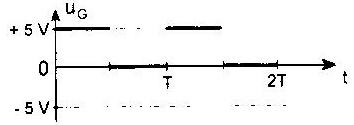

Quelle courbe peut représenter la tension u_R aux bornes de la résistance ?

---

 corrigé

---

La tension u_R et l'intensité du courant traversant la résistance, sont proportionnelles : les courbes u_R = f(t) et I= g(t) ont donc la même allure.

De plus lors de la décharge du condensateur à travers la résistance, le courant change de sens.

Lors de la charge l'intensité décroît de manière exponentielle.

En fin de charge, comme en fin de décharge, l'intensité du courant est nulle.

La courbe a possède ces propriétés.

---

A la date t=0, on branche un générateur idéal de tension, de f.e.m E aux bornes d'un dipôle constitué d'un conducteur ohmique de résistance R, d'une bobine d'inductance L et de résistance interne négligeable. On note u(t) la tension aux bornes de la bobine.

Quelle(s) est (sont) le(s) affirmation(s) exacte(s) ?

1. u(t) vérifie l'équation différentielle u + L/R u'= 0
2. u(t) vérifie l'équation différentielle u/(RL) + u"=0.
3. u(t) est une fonction sinusoïdale du temps.
4. en régime permanent u(t) = 0
5. en régime permanent u(t) = E

Un circuit est constitué d'un condensateur de capacité C₀ = 2,0 mF, d'une bobine d'inductance L= 10 mH, d'un condensateur de capacité C= 5,0 mF et d'un interrupteur K. Les condensateurs sont initialement déchargés. Le condensateur C₀ est alors chargé sous une tension de 12 V puis le générateur est débranché. A l'instant t=0, on ferme l'interrupteur K.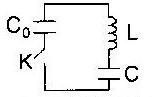

Que vaut la période ( ms) des oscillations ? ( 0,53 ; 0,75 ; 0,89 ; 1,4 ; 1,7)

---

 corrigé

---

capacité C_éq du condensateur équivalent à deux condensateurs en série : C_éq = C₀C/(C₀+C) = 2*5/(2+5)= 10/7 mF

période : 2p[LC_éq]^½ =6,28 [0,01 *10/7 10^-6]^½ = 7,5 10^-4 s = 0,75 ms.

---

Un circuit RLC série est alimenté par une tension sinuso<îdale de fréquence réglable, de valeur efficace U ; l'inrensité efficace est notée I et l'impédance est notée Z. Pour la fréquence f₀, le circuit est dit résonant. L'intensité efficace à la résonance est notée I₀.

Quelle(s) est (sont) le(s) affirmation(s) exacte(s) ?

1. Pour une fréquence quelconque, la puissance consommée est P= RI².
2. Pour une fréquence quelconque, la puissance consommée est P= R(U/Z)².
3. Pour une fréquence f₀, la puissance consommée est P= RI₀².
4. La puissance consommée est minimale quand Z= R.
5. La puissance consommée par le condensateur est nulle.

Le nucléide cadmium ¹⁰⁷₄₈ Cd est radioactif. Sa désintégration donne l'argent et une particule chargée. Sa demi-vie est T= 6 h 42 min. Au bout de combien de temps ( heure et minutes) 75% du cadmium initial se sera t-il désintégré ? ( 1 h 41 min ; 3 h 21 min ; 5 h 2 min ; 10 h 3 min ; 13 h 24 min)

La réaction de fission de l'uranium 235 se produit suivant : ²³⁵₉₂U + ¹₀n -->¹⁴⁰₅₂Te+ ⁹³₄₀Zr + 3¹₀n.

Les énergies de liaison par nucléons en MeV sont données ci-dessous :

23592U	14052Te	9340Zr
7,5	8,6	8,3

N_A= 6,02 10²³ mol^-1 ; e = 1,6 10^-19 C.

Quel est le temps (jours) au bout duquel, dans une tranche de centrale nucléaire de 1MW électrique, 1 kg d'uranium 235 a été transformé en produits de fission si le rendement énergétique thermique- électrique est de 33 % ? (134 ; 140 ; 267 ; 312 ; 334 ).