Production d'une onde sonore bac S Antilles 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

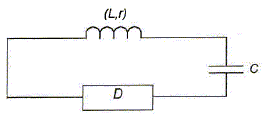
Pour produire une onde sonore périodique sinusoïdale de fréquence f, on réalise au laboratoire une chaîne constituée : d'un circuit électrique oscillant, d'un amplificateur de tension et d'un haut parleur. Etude du circuit électrique oscillant : inductance de la bobine L= 0,50 H, résistance de la bobine r = 12 W ; capacité du condensateur C=1,0 mF. Le dipole D entretient les oscillations électriques. Pour obtenir des oscillations électriques de fréquence donné, on réalise dans un premier temps, avec les composants précédents, sans le dipole D, le montage schématisé ci-dessous. 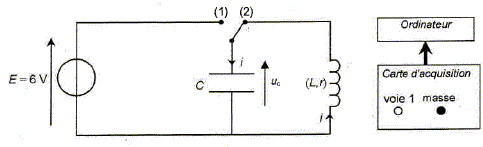Quand l'interrupteur est en position 1, le condensateur se charge sous la tension E. A la date t=0 on commute l'interrupteur en position 2. On obtient la courbe uC=f(t) ci-dessous : Pour visualiser la tension uC aux bornes du condensateur, représenter les connexions de la voie 1 et de la masse de la carte d'acquisition. Pourquoi qualifie t-on le régime de la tension uC de speudopériodique ?  La courbe observée est périodique : l'amplitude des oscillations diminue lentement au cours du temps. 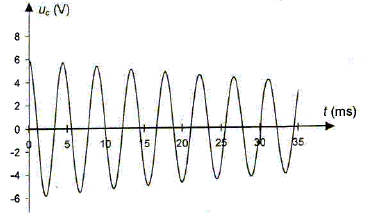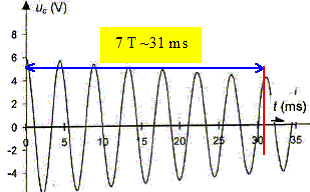Déterminer graphiquement la pseudo-période T et en déduire la fréquence f. T = 31/7 = 4,4 ms T = 4,4 10-3 s. f= 1/T = 1/4,4 10-3 f = 2,3 102 Hz. On peut assimiler la pseudopériode à la période propre T0 du dipole LC. Rappeler l'expression de T0, la calculer et comparer à T. T0 = 2p[LC]½. = 6,28 [0,50*10-6]½ T0 = 4,4 10-3 s. T et T0 sont égales si on tient compte de la précision des données. 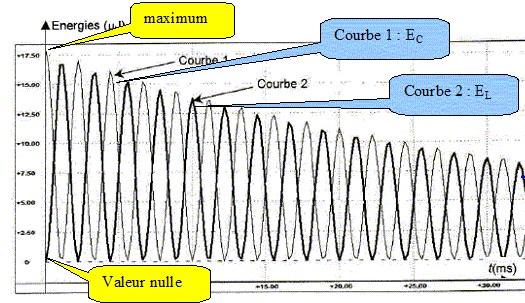A l'aide d'un tableur on trace l'évolution temporelle des énergies emmagasinées dans le condensateur et dans la bobine EC et EL. Donner l'expression de EC. ½Cu2C. Donner l'expression de EL en fonction de l'intensité i du courant dans le circuit. ½Li2. Identifier les courbes en justifiant. Initialement le condensateur est chargé et stocke toute l'énergie du dipole. ( voir graphe ci-dessus). L'énergie totale E emmagasinée dans le circuit représente la somme des énergie EC et EL. Comment évolue t-elle au cours du temps ? Quelle est la cause de cette perte d'énergie ? Lors des échanges d'énergie entre condensateur et bobine, une partie de cette énergie est perdue par effet Joule dans la partie résistive de la bobine : l'énergie E diminue donc au cours du temps. .On s'intéresse au circuit oscillant suivant : Expliquer du point de vue énergétique le rôle du dipôle D. Le dipôle D compense à chaque instant les pertes d'énergie. Comment évolue alors la tension uC aux bornes du condensateur ? régime sinusoïdal non amorti. 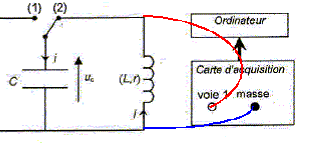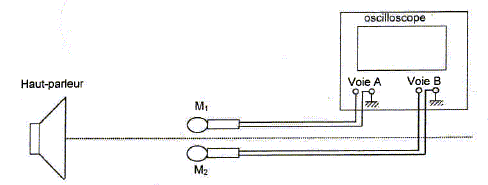Mesure de la célérité du son émis par le haut-parleur. Le signal électrique obtenu avec le circuit oscillant précédent est amplifié puis transformé en onde sonore par le haut parleur. 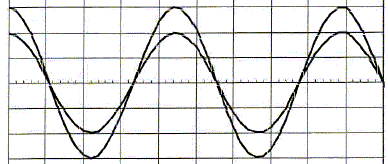Pour mesurer la vitesse du son émis par le haut parleur à la température de la salle, on réalise l'expérience schématisée ci-dessous : On place côte à côte face au haut parleur, deux microphones M1 et M2 branchés sur les voies A et B d'un oscilloscope. Les courbes observées sont représentées ci-dessous : Les deux voies de l'oscilloscope ne sont pas réglées sur la même sensibilité verticale. Quelle est la nature de l'onde sonore émise par le haut-parleur ? Onde mécanique progressive longitudinale. Cette onde est-elle longitudinale ? Expliquer cette appellation. La direction de propagation de l'onde et la direction de la perturbation sont parallèles. Les courbes observées sur l'écran de l'oscilloscope sont en phase. On laisse le microphone M1 en place et on déplace lentement et parallèlement à l'axe du haut parleur le microphone M2 jusqu'à obtenir à nouveau les deux courbes en phase. La distance qui sépare les deux microphones dans cette nouvelle position est d= 1,50 m. Définir la longueur d'onde d'une onde périodique. Distance, exprimée en mètre, parcourue par le front de l'onde pendant une période T. Que représente la distance d dans cette expérience ? M1 et M2 étant dans le même état vibratoire, sont déparer par un nombre entier de longueur d'onde. d représente la longueur d'onde l. Calculer la vitesse de propagation du son dans l'air si la fréquence du son est f = 225 Hz. v =l f. v =1,50*225 v = 338 m/s.

retour -menu