Stockage de l'énergie solaire : condensateur, pile à combustible bac S Nlle Calédonie 03/2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

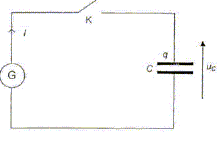
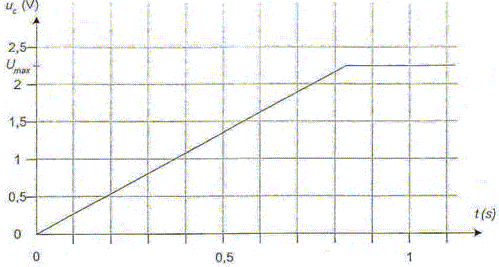
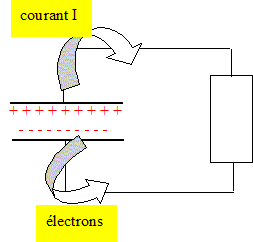
" Le Soleil est une étoile quelconque mais, pour la vie sur Terre, sa présence est indispensable…L'énergie solaire reçue par la Terre représente par an près de 15 000 fois la totalité de la consommation énergétique mondiale actuelle ! " (CRDP Nantes) Une partie de cette énergie abondante peut être transformée en énergie électrique par une cellule photovoltaïque (capteur solaire). Cette énergie électrique doit être stockée car la demande énergétique peut être décalée dans le temps vis-à-vis de l'apport en énergie solaire (utilisation par exemple, d'un éclairage la nuit). Dans cet exercice, on étudie deux types de stockage de l'énergie électrique fournie par une cellule photovoltaïque : - le stockage de l'énergie électrique dans un condensateur de grande capacité. - la production par électrolyse d'un combustible pour une pile électrochimique. Les deux parties correspondant aux deux types de stockage sont indépendantes. La charge et la décharge du condensateur peuvent être traitées indépendamment. Utilisation d'un condensateur de très grande capacité. Le fabriquant du condensateur utilisé indique une valeur de capacité C = 100 000 µF 10%. Charge du condensateur à courant constant. Les caractéristiques de la cellule photovoltaïque en régime normal de fonctionnement sont indiquées ci-dessous (toutes les données ne sont pas utiles) : Puissance : 0,6 W ; intensité : 270 mA ; tension maximale : 2,25 V ; dimensions : 394 * 127* 20 mm. Masse : 0,41 kg ; plage de température : - 40 °C à + 60 °C. La cellule photovoltaïque se comporte comme un générateur G débitant un courant d'intensité constante I = 0,27 A, tant que la tension à ses bornes reste inférieure à la tension maximale Umax = 2,25 V.       La cellule photovoltaïque est branchée aux bornes du condensateur. A la date t0 = 0 s, on ferme l'interrupteur K et on débute l'enregistrement informatisé des variations de la tension aux bornes du condensateur uC(t) en fonction du temps. On obtient le graphe suivant :   Nommer les deux régimes observables sur le graphe uC = f(t) représenté ci-dessus. De 0 à 0,84 s, le condensateur initialement déchargé, se charge, la tension à ses bornes croît. De 0,84 s et au delà, le condensateur est chargé, la tension à ses bornes reste constante. Donner l'expression de uC en fonction de C et de la charge q du condensateur. La charge q et la tension uC aux bornes du condensateur sont proportionnelles : la constante de proportionalité est la capacité C. q= Cuc soit uc=q/C. (1) Le condensateur est initialement déchargé. Donner l'expression de la charge du condensateur q en fonction de l'intensité I et de la date t lorsque uC est inférieure à Umax (charge à courant constant). L'intensité étant constante la cgarge q et l'intensité sont proportionnelles. q=It. (2) En déduire que uC =I t/C tant que uC est inférieure à Umax. (1) et (2) conduisent à : Cuc= It soit uc=I/C t. (3) Déterminer la valeur et préciser l'unité du coefficient directeur, noté k, de la portion de droite de la figure ci-dessus lorsque uC est inférieure à Umax . Utiliser ce résultat pour vérifier que la valeur de C est compatible avec les indications du constructeur. k = I/C avec I = 0,27 A ; C =I/k = 0,27/2,75 = 9,8 10-2 F. Le constructeur indique 0,1 F à + ou - 10% près soit C comprise entre 0,09 et 0,11 F. Il y a donc compatibilité entre la valeur déterminée ci-dessus et l'indication du constructeur. Calculer la quantité d'énergie électrique stockée dans le condensateur lorsque la charge est terminée. E = ½CU2 max = 0,5*0,1*2,252 =0,25 J. Décharge du condensateur dans un conducteur ohmique.     L'énergie stockée dans le condensateur peut être utilisée pour faire fonctionner une lampe (L) de faible puissance que l'on assimile à un conducteur ohmique de résistance R. On branche en série le condensateur et le conducteur ohmique. A l'instant de date t = 0, le condensateur a une tension à ses bornes égale à Umax et on ferme l'interrupteur K'. Le graphe donnant uC = f(t) est donné . 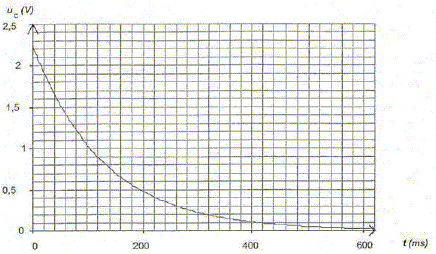En respectant les conventions de la figure, établir l'expression de i en fonction de uC. uc + Ri = 0. (4) Montrer que l'expression de l'équation différentielle à laquelle satisfait uC lors de la décharge peut s'écrire ; uC + RCduc/dt = 0. i = dq/dt et q = Cuc soit i = C duc/dt ; repport dans (4) : uC + RCduc/dt = 0.(5) Vérifier que uC = Umax exp( - t/ (RC)) est une solution de l'équation différentielle précédente. uC = Umax . exp( - t/ (RC)) ; duc/dt = Umax / (-RC) exp( - t/ (RC)) puis repport dans (5) Umax . exp( - t/ (RC)) + RC Umax / (-RC) exp( - t/ (RC)) =0 Umax . exp( - t/ (RC)) - Umax exp( - t/ (RC)) =0 est vérifié quel que soit t. Quel est le signe de i(t) lors de la décharge ? Justifier la réponse. Le courant de décharge est de sens contraire au courant de charge. 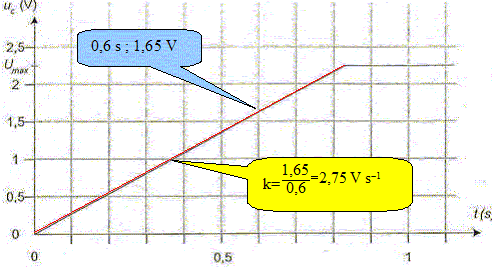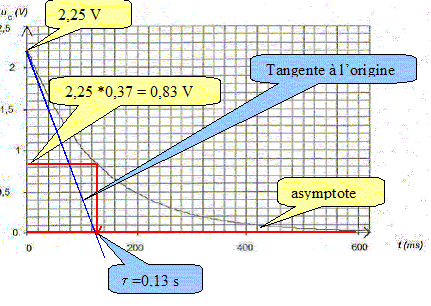Déterminer, en faisant apparaître clairement la méthode sur la figure la valeur de la constante de temps t du système électrique. 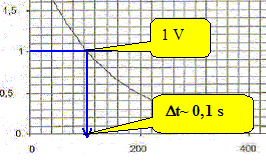Déduire de la valeur de la constante de temps t la valeur de la résistance R. t= RC avec C= 0,1 F et t = 0,13 s d'où R = t /C =0,13 /0,1 = 1,3 W. On considère que la lampe (L) fonctionne correctement si la tension imposée par le condensateur entre ses bornes est supérieure à 1,0 V. On rappelle que l'on assimile la lampe au conducteur ohmique de résistance R. Déterminer, en utilisant la figure la durée Dt durant laquelle la lampe fournit une quantité de lumière suffisante. Conclure sur l'utilisation de ce condensateur pour un éclairage la nuit. Dt est trop petit : le condensateur se décharge trop vite et ce dispositif ne peut convenir pour un éclairage de nuit. 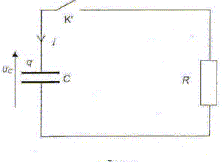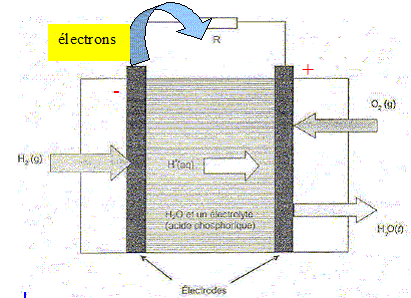Utilisation d'une pile à combustible. L'énergie électrique fournie par une cellule photovoltaïque permet la production de dihydrogène gazeux H2(g) par électrolyse de l'eau. Le dihydrogène produit est stocké, puis utilisé dans une pile à combustible. Électrolyse de l'eau. Afin de réaliser l'électrolyse de l'eau, les bornes de la cellule photovoltaïque sont reliées à deux électrodes de platine immergées dans une solution d'acide sulfurique. Les gaz formés sont récupérés. L'équation modélisant la transformation ayant lieu lors de l'électrolyse est : 2 H2O( l) = 2H2(g) + O2(g) Les couples oxydant/réducteur mis en jeu sont O2(g) / H2O(l ) et H+(aq) / H2(g). L'électrolyse de l'eau est-elle une transformation spontanée ? Justifier. Non : une électrolyse est une transformation forcée qui nécessite un apport d'énergie sous forme électrique. Ecrire les deux équations d'oxydoréduction correspondant aux transformations ayant lieu aux électrodes. Quel type de réaction a lieu à l'électrode reliée à la borne négative de la cellule photovoltaïque ? Nommer cette électrode. Réduction à la cathode négative : 2H+(aq)+ 2e- =H2(g) Oxydation de l'eau à l'anode positive : 2H2O(l ) = O2(g) + 4e- +4H+(aq) Fonctionnement de la pile. Après douze heures de fonctionnement, l'électrolyseur a produit une quantité de dihydrogène n(H2)=6,0 10-2 mol. Ce dihydrogène est entièrement utilisé comme combustible dans une pile schématisée ci-dessous. La pile consomme, lors de son fonctionnement, du dihydrogène et du dioxygène gazeux qui sont introduits au contact d'électrodes poreuses séparées par une solution acide jouant le rôle d'électrolyte. Le seul produit formé est de l'eau. L'équation modélisant la transformation ayant lieu est : 2 H2(g) + O2(g) = 2 H2O(l ). La valeur d'un faraday est F = 9,65 104 C.mol -1. Indiquer sur la figure les bornes positive et négative du générateur ainsi que la nature et le sens de circulation des porteurs de charges hors de la pile. Le dihydrogène joue le rôle de réducteur : il s'oxyde suivant : H2(g) = 2H+(aq)+ 2e- . Cette électrode est une anode ( oxydation) négative ( des électrons sont libérés).   Donner l'expression de la quantité d'électrons n(e -) échangée lors de la " combustion " de la quantité n(H2) de dihydrogène dans la pile. En déduire la valeur de la quantité d'électricité Q échangée. H2(g) = 2H+(aq)+ 2e- . n(e-) = 2 n(H2)=2*6,0 10-2 =0,12 mol. Q = n(e-) F = 0,12*9,65 104 =1,158 104 ~1,16 104 C. La pile permet de faire fonctionner correctement la lampe (L) avec une tension à ses bornes de 1,0 V et une intensité constante du courant de 0,70 A. Déterminer la durée de fonctionnement de la pile pour cette intensité. Commenter ce résultat en comparant cette durée à celle obtenue ci-dessus. Dt = Q/I =1,158 104 / 0,70 = 1,6 104 s = 4,6 h. Durée très supérieure à la valeur obtenue lors de la décharge du condensateur : cette pile peut alimenter une lampe assurant un éclairage nocturne.

retour -menu