Stabilisation des mouvements d'une tour concours technicien météo 2008. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts

. .

. .

Pour construire des tours de plus en plus hautes, on utilise des matériaux de plus en plus légers et souples. Ces constructions peuvent alors se mettre à osciller dangereusement en cas de tremblement de terre ou sous l'action de fortes rafales de vent. Les oscillations peuvent encore être amplifiées par un phénomène de résonance. Pour limiter ces oscillation, il suffit d'installer au sommet des tours un oscillateur résonnant muni d'un dispositif d'amortissement. 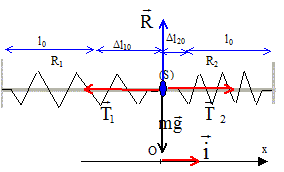Partie 1 : étude d'un oscillateur mécanique. Soit un système de masse m astreint à glisser le long d'une tige horizontale de direction Ox. Ce mobile est maintenu par deux ressorts à spires non jointives sont les extrémités sont accrochées à deux points fixes A et B. Les deux ressorts sont identiques, ont même constante de raideur k et même longueur au repos l0. A l'équilibre, le centre d'inertie G du système est en O et les deux ressorts ont la même longueur L > L0. On étudie le système dans le référentiel terrestre, considéré comme galiléen. Les frottements sont négligeables. A t=0, le système est écarté de sa position d'équilibre, le point G étant à l'abscisse x0, et abandonné sans vitesse initiale. Faire le bilan des forces appliquées au système à t=0. les représenter. L'action R de la tige et poids P se neutralisent. Ressort n°1 : longueur L1 = L + x ; valeur de la tension de ce ressort : T1 = k((L+x-L0) Ressort n°2 : longueur L2 = L - x ;valeur de la tension de ce ressort : T2 = k((L-x-L0) A la date t=0, remplacer x par x0. Montrer que le dispositif est équivalent à un seul ressort de raideur K= 2k. Ecrire la seconde loi de Newton sur l'axe horizontal, orienté vers la droite : -T1+T2 = m x" -k((L+x-L0) +k((L-x-L0) = m x" -2kx = mx" soit mx" + 2k x=0. (1) équation différentielle d'un oscilateur élastique de raideur K= 2k.   Montrer que l'équation différentielle du mouvement est : x" + K m x =0 (1) s'écrit en divisant chaque terme par la masse m : x" + K/m x = 0. Montrer que cette équation admet une solution du type x(t) = Xm cos (wt). Exprimer Xm et w en fonction de K, m et x0. dériver deux fois x(t) par rapport au temps : x'(t) = - Xmw sin (wt). x"(t) = - Xmw2 cos (wt) = -w2 x(t). Repport dans (1) : -w2 x(t)+ K/m x(t) = 0 Cette égalité est vérifiée quel que soit le temps si : w2 = K m A t = 0 x(0) = x0 d'où : Xm = x0.  A l'aide d'une analyse dimensionnelle, vérifier que l'expression suivante peut correspondre à la période T des oscillations du système. T =2p [ m K ]½ 2p est sans dimension ; m : masse en kg ou encore [m]= M K :raideur ou force divisée par une longueur [K]= force longueur-1. Or une force est une accélération fois une masse une accélération est une longueur divisée par le carré d'un temps, d'où [force]=M L T-2. Par suite : [K]= M T-2 et : m K = 1 T-2 = T2 ; m½ K½ a la dimension d'un temps   Quelle relation existe t-il entre T et w ? T = 2p w   Etude énergétique. Sous quelle forme d'énergie se trouve le système à l'état initial ? Donner son expression en fonction de K, m et x0. L'énergie mécanique de l'oscillateur est sous forme potentielle élastique. L'origine de cette énergie est prise à la position d'équilibre. Epé = ½K x02 Que peut-on dire de l'énergie mécanique du système au cours du temps ? En absence de frottement, l'énergie mécanique reste constante. Sous quelle forme d'énergie se trouve le système à t = 0,25 T ? Où se trouve alors le centre d'inertie du système ? L'énergie mécanique est sous forme cinétique ; le centre d'inertie du système se trouve à la position d'équilibre. 2è partie : application à l'oscillateur résonant d'une tour. En cas de rafale de vent supérieure à 100 km/h, la tour se met à osciller avec une fréquence d'environ f = 0,2 Hz. On admettra que les oscillations ont lieu dans un seul plan vertical. En l'absence de dispositif d'amortissement, l'amplitude initiale des oscillations est de 40 cm au sommet de la tour et ne diminue que de 1% par période, les oscillations vont ainsi durer 10 minutes. L'oscillateur du dispositif d'amortissement est conçu de telle sorte que sa fréquence propre soit identique à celle de la tour, l'énergie se répartit alors sur les deux oscillateurs ce qui réduit l'amplitude initiale des oscillations de la tour de 40 %. En outre les oscillations s'amortissent plus rapidement, de 10 % par période. Quelle est la période des oscillations de la tour ? T= 1 f = 1 0,2 = 5 s. En l'absence d'amortissement combien y aurait-il d'oscillations ? 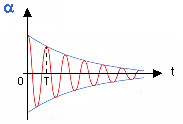Les oscillations durent 10 min soit 10*60 = 600 secondes. Par suite il y a : 600 / 5 = 120 oscillations. Quelle est l'amplitude initiale des oscillations au sommet de la tour en présence du dispositif d'amortissement ? "réduit l'amplitude initiale des oscillations de la tour de 40 % " d'où la réduction de l'amplitude : 40 *0,4 = 16 cm. Amplitude initiale : 40-16 = 24 cm. Montrer qu'au bout de 3 périodes l'amplitude des oscillations est inférieure à 18 cm au sommet de la tour. temps ( en période) amplitude initiale (cm) réduction amplitude finale T 24 2,4*0,1 = 2,4 cm 24-2,4 = 21,6 cm 2T 21,6 21,6*0,1 = 2,16 cm 21,6-2,16 ~19,4 cm 3T 19,4 cm 19,4*0,1=1,9 cm 19,4-1,9 =17,5 cm. Représenter l'allure de la courbe donnant la position du sommet de la tour au cours du temps par rapport à sa position d'équilibre. L'oscillateur du dispositif d'amortissement est constitué d'une masse M=400 t, placé sur une couche d'huile. Il obéit aux même lois que le système étudié dans la première partie. Quelle est le rôle de la couche d'huile ? En l'absence d'huile la masse M resterait immobile. La couche d'huile, en diminuant l'adhérence, permet à la masse M de se déplacer sur le sol ; ce déplacement s'effectue avec des frottements relativement importants. Déterminer l'ordre de grandeur de la raideur k de chacun des ressorts retenant la masse M. ( on prendra pi2 = 10). T2= 4 p2 M 2k ; k = 4 p2 M 2T2 k= 4*10*4 105 2*52 = 3,2 105 N m-1.

retour -menu