Poussée d'Archimède lycée. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Archimède confondit un jour un orfèvre qui avait vendu une couronne d'or coupée d'argent. Dans une bassine d'eau pleine à ras bord, il plonge une mesure d'argent puis une mesure d'or de poids égaux à celui de la couronne. Il mesure les débordements successifs, puis plonge enfin la fameuse couronne. On donne les masses volumiques ror = 19,3 g cm-3 ; ragent = 10,5 g cm-3. Soient V, V1, V2 les volumes d'eau déplacés respectivement par la couronne, la mesure d'or, et la mesure d'argent. Comparer ces trois volumes et justifier. Un volume (cm-3) est égal à une masse (g) divisée par une masse volumique (g cm-3) V = m r Pour une même masse, le volume est d'autant plus grand que la masse volumique est plus petite. ror > rcouronne > ragent donc : V1< V< V2. La masse de la couronne est m = 3,0 kg et le volume d'eau qu'elle déplace est V= 0,20 L. Calculer la masse volumique de la couronne ( g cm-3 ). 3 kg = 3000 g ; 0,2 L = 200 cm3 ; r = m V = 3000 200 = 15 g cm-3   Calculer le volume d'eau déplacé par la mesure d'or puis par la mesure d'argent. V2 = m rargent = 3000 10,5 = 286 cm3 V1 = m ror = 3000 19,3 = 155 cm3 . . Le ludion. Le ludion est un petit personnage solidaire d'une sphère imperméable, de volume variable, renfermant de l'air. Il est placé dans une éprouvette cylindrique verticale de hauteur très supérieure aux dimensions du ludion. L'éprouvette est remplie d'eau sur une hauteur h et fermée à sa partie supérieure par une membrane souple imperméable. Lorsque l'on appuie pas sur la membrane, le ludion est en équilibre en un point voisin de la surface de l'eau. Lorsque l'on appuie sur la membrane, on constate que le ballon tombe au fond de l'éprouvette. Données : g = 9,8 N/kg ; l'eau est imcompressible et sa masse volumique vaut r= 103 kg m-3 ; volume de la sphère V = 1 cm3 ; le volume du personage est négligeable devant celui de la sphère ; masse du ludion m= 1 g. La membrane est libre et le ludion est en équilibre ; le volume de la sphère est 1 cm3. Donner les caractéristiques de la poussée d'Archimède exercée sur le ludion. La poussée est appliquée au centre de la sphère ; sa direction est la verticale, son sens est vers le haut et sa valeur est égale au poids du volume d'eau déplacé. F = r g V avec V = 1 cm3 = 10-6 m3 ; g = 9,8 N/kg et r = 103 kg m-3. F = 103 *9,8 * 10-6 = 9,8 10-3 N. Donner les caractéristiques du poids du ludion. Comparer la valeur du poids et celle de la poussée. Le poids est appliquée au centre de la sphère ; sa direction est la verticale, son sens est vers le bas et sa valeur est égale à : P= mg avec m = 1 g = 10-3kg. P= 10-3*9,8 = 9,8 10-3 N. Le poids et la poussée ont même valeur : les deux forces se neutralisent et le ludion est en équilibre. On appuie sur la membrane, le volume de la sphère devient V2 = 0,6 cm3. La température de l'air ( entre la membrane et l'eau) restant constante, expliquer pourquoi la pression de l'air augmente. La membrane est imperméable ( pas de fuite d'air) et la température est constante : en conséquence le produit pression * volume reste constant. Or en appuyant sur la membrane on fait diminuer le volume d'air compris entre l'eau et la membrane. En conséquence la pression de l'air situé entre la membrane et le liquide augmente. La température de l'air ( dans la sphère) restant constante, expliquer pourquoi le volume de la sphère diminue. L'eau transmet à la sphère la variation de pression subie en surface. La sphère est imperméable ( pas de fuite d'air) et la température est constante : en conséquence le produit pression * volume reste constant. A une augmentation de pression correspond une diminution du volume de l'air de la sphère. Déterminer la valeur des forces extérieures agissant sur le ludion et justifier la descente. ( On négligera les frottements entre le ludion et l'eau). Le ludion est soumis à son poids et à la poussée d'Archimède. Le poids est resté constant, mais la poussée prend la nouvelle valeur : F = r g V2 avec V2 = 0,6 cm3 =6 10-7 m3 ; g = 9,8 N/kg et r = 103 kg m-3. F = 103 *9,8 * 6 10-7 = 5,9 10-3 N. La poussée étant inférieure au poids, le ludion n'est plus en équilibre : le poids l'emporte sur la poussée et le ludion descend. 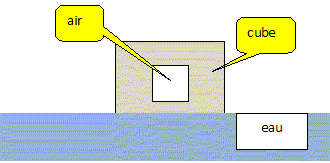Un cube pelin de côté a= 10 cm flotte à la surface de l'eau. Il est immergé au 3/4 de sa hauteur. Masse volumique de l'eau : reau = 1 g cm-3. Quelle est la masse volumique r du cube. Le cube est en équilibre sous l'action de son poids et de la poussée d'Archimède. Ces deux forces opposées ont la même valeur. On note V= a3 le volume total du cube et Vi = 0,75 a3 le volume immergé. poids : P= mg avec m = r V = ra3 ; P = ra3 g. Poussée : poids du volume de fluide déplacé : F = reauVi g = reau 0,75 a3 g. par suite : ra3 g = reau 0,75 a3 g ; r= reau (0,75) = 0,75 g cm-3. Le cube précédent a été creusé. Lorsque ce cube flotte, seule 1/4 de sa hauteur est immergée. Quelle est la masse du cube ? Le cube est en équilibre sous l'action de son poids et de la poussée d'Archimède. Ces deux forces opposées ont la même valeur. On note V= a3 le volume total du cube et Vi = 0,25 a3 le volume immergé. Poussée : poids du volume de fluide déplacé : F = reauVi g = reau 0,25 a3 g. Poids du cube( matériau+ air emprisonné) : P= Mg. par suite : M g = reau 0,25 a3 g ; M = reau 0,25 a3 =1*0,25 *103 = 250 g. Calculer le volume d'air emprisonné dans le cube. Volume du matériau constituant le cube : La masse volumique de l'air étant très inférieure à celle du matériau constituant le cuivre, on peut négliger la masse de l'air devant celle du solide. Vmat = M r = 250 0,75 = 333 cm3. Volume total du cube : a3 = 103 = 1000 cm3. Volume d'air : 1000-333 = 667 cm3. Que vaut l'épaisseur de la paroi du cube ? Côté du trou cubique : prendre la racine cubique du volume d'air : 6671/3 = 8,74 cm. a = épaisseur du matériau + côté du trou + épaisseur du matériau Deux épaisseurs du matériau = a -8,74 = 10-8,74 = 1,26 cm épaisseur = 1,26/2 =0,63 cm = 6,3 mm.

retour -menu